Se cinquanta milioni di persone affermano una cosa sciocca, essa resta comunque una cosa sciocca.
Anatole France
Stomachion
lunedì 28 luglio 2014
Amici immaginari
martedì 22 luglio 2014
I sotterranei
Devo dire che con questo libro Jack mi ha un po' sfidata, non per i contenuti ma per come è scritto: soprattutto nella prima parte si poteva incontrare un punto (in senso di punteggiatura) anche dopo una pagina e mezza, e in quella pagina e mezza passare da diversi eventi, incontri, situazioni. Una sfida che ho accolto e apprezzato, perché è una bella storia d'amore ma senza troppi fronzoli (forse è proprio l'assenza di fronzoli che ai tempi questo libro non fu ben accolto dalla critica, anzi fu processato!), una bella storia di vita. E poi che dire, Jack è sempre il meraviglioso Jack!
domenica 20 luglio 2014
sabato 19 luglio 2014
Tre ombre
Non ricordo più per quale motivo la recensione non è arrivata su LSB con il suo iter regolare, ma avendola ritrovata, la recupero per DropSea:
Le favole hanno da sempre il potere di veicolare in maniera semplice ma diretta alcuni messaggi importanti: non dare confidenza agli sconosciuti, stare attenti ai pericoli della vita. A volte, però, la vita è piena di eventi per noi incontrollabili e le favole possono aiutare a sopportarli. In un certo senso è quello che accade con Tre ombre di Cyril Pedrosa, cartoonist francese formatosi presso la Disney e che si presenta con quest'opera con uno stile grafico che risulta una sintesi tra Cavazzano e Uderzo, ottenendo uno stile interessante e che in alcuni punti richiama i nostri Mottura e Celoni, anch'essi disneyani doc.
Molto kingiano l'inizio della storia: una famiglia (padre, madre e figlioletto) vive in un angolo tranquillo della campagna, lontano dalla città, in un'atmosfera bucolica ma non noiosa per il piccolo. Un giorno, però, questa tranquillità viene spezzata dall'arrivo di tre ombre misteriose: esse sono venute per portare via il piccolo Joachim.
Iniziano discussioni e litigi tra marito e moglie: la madre sembra accettare più semplicemente il distacco dal figlio, mentre il padre cerca di opporsi all'inevitabile avvicinarsi delle tre ombre: così una mattina, insieme a Joachim, inizia la fuga. La parte più importante del loro viaggio avviene su una nave, che deve attraversare il "grande fiume", l'oceano: stipati tra le assi dell'imbarcazione come nei viaggi della speranza dei primi coloni verso il nuovo mondo, i due protagonisti trovano sintetizzato in quel microcosmo un po' tutto il mondo, con le sue solidarietà, le sue brutture, le sue violenze.
Il viaggio sulla nave diventa, quindi, una sorta di metafora della vita, e la tempesta in cui la nave naufraga, conclusione di una lunga scena di violenza e vendetta, sembra metafore dell'autodostruzione della società umana: in questo senso il tentativo finale di salvare il proprio figlio gettandosi tra le acque rappresenta la speranza che, in ogni momento, resta sempre accesa. E poi il sacrificio che il padre compie per salvare il figlio, donando il proprio cuore a un uomo malvagio: questi costruirà la propria fortuna proprio su questo dono, quasi come gli uomini di potere che costruiscono la loro posizione sulla fiducia donata loro dal lavoro e dalla fatica dei più umili.
L'intervento finale dei tre spiriti, infine, riporta il cuore al suo posto, grazie al quale il padre di Joachim comprenderà i propri errori, lasciando così andare via il proprio figlio per tornare alla sua casa, da sua moglie.
Un'opera fantastica in cui Pedrosa esplora in maniera inusuale e per certi versi originale le difficoltà dei genitori nel dover affrontare la morte di un figlio, nel dovergli dire addio: in questo caso è servito un lungo e difficilissimo viaggio, ricco di pericoli e di incontri ambigui. Solo la vita e la sua bellezza danno la forza di andare avanti, e questo sembra il messaggio di un disneyano francese di successo.
Del volume, recentemente riproposto dalla BD in una nuova edizione è stato "brevisionato" da Guglielmo Nigro per LSB
Le favole hanno da sempre il potere di veicolare in maniera semplice ma diretta alcuni messaggi importanti: non dare confidenza agli sconosciuti, stare attenti ai pericoli della vita. A volte, però, la vita è piena di eventi per noi incontrollabili e le favole possono aiutare a sopportarli. In un certo senso è quello che accade con Tre ombre di Cyril Pedrosa, cartoonist francese formatosi presso la Disney e che si presenta con quest'opera con uno stile grafico che risulta una sintesi tra Cavazzano e Uderzo, ottenendo uno stile interessante e che in alcuni punti richiama i nostri Mottura e Celoni, anch'essi disneyani doc.
Molto kingiano l'inizio della storia: una famiglia (padre, madre e figlioletto) vive in un angolo tranquillo della campagna, lontano dalla città, in un'atmosfera bucolica ma non noiosa per il piccolo. Un giorno, però, questa tranquillità viene spezzata dall'arrivo di tre ombre misteriose: esse sono venute per portare via il piccolo Joachim.
Iniziano discussioni e litigi tra marito e moglie: la madre sembra accettare più semplicemente il distacco dal figlio, mentre il padre cerca di opporsi all'inevitabile avvicinarsi delle tre ombre: così una mattina, insieme a Joachim, inizia la fuga. La parte più importante del loro viaggio avviene su una nave, che deve attraversare il "grande fiume", l'oceano: stipati tra le assi dell'imbarcazione come nei viaggi della speranza dei primi coloni verso il nuovo mondo, i due protagonisti trovano sintetizzato in quel microcosmo un po' tutto il mondo, con le sue solidarietà, le sue brutture, le sue violenze.
Il viaggio sulla nave diventa, quindi, una sorta di metafora della vita, e la tempesta in cui la nave naufraga, conclusione di una lunga scena di violenza e vendetta, sembra metafore dell'autodostruzione della società umana: in questo senso il tentativo finale di salvare il proprio figlio gettandosi tra le acque rappresenta la speranza che, in ogni momento, resta sempre accesa. E poi il sacrificio che il padre compie per salvare il figlio, donando il proprio cuore a un uomo malvagio: questi costruirà la propria fortuna proprio su questo dono, quasi come gli uomini di potere che costruiscono la loro posizione sulla fiducia donata loro dal lavoro e dalla fatica dei più umili.
L'intervento finale dei tre spiriti, infine, riporta il cuore al suo posto, grazie al quale il padre di Joachim comprenderà i propri errori, lasciando così andare via il proprio figlio per tornare alla sua casa, da sua moglie.
Un'opera fantastica in cui Pedrosa esplora in maniera inusuale e per certi versi originale le difficoltà dei genitori nel dover affrontare la morte di un figlio, nel dovergli dire addio: in questo caso è servito un lungo e difficilissimo viaggio, ricco di pericoli e di incontri ambigui. Solo la vita e la sua bellezza danno la forza di andare avanti, e questo sembra il messaggio di un disneyano francese di successo.
Del volume, recentemente riproposto dalla BD in una nuova edizione è stato "brevisionato" da Guglielmo Nigro per LSB
venerdì 18 luglio 2014
Dimostrazioni senza parole: differenze tra cubi
\[(n+1)^3 - n^3 \equiv 1 \mod 6\]

Claudi Alsina,, Roger Nelsen,, & Hasan Unal (2014). Proof Without Words: The Difference of Consecutive Integer Cubes Is Congruent to 1 Modulo 6 The College Mathematics Journal, 45 (2), 135-135 DOI: 10.4169/college.math.j.45.2.135 (facebook)

Claudi Alsina,, Roger Nelsen,, & Hasan Unal (2014). Proof Without Words: The Difference of Consecutive Integer Cubes Is Congruent to 1 Modulo 6 The College Mathematics Journal, 45 (2), 135-135 DOI: 10.4169/college.math.j.45.2.135 (facebook)
giovedì 17 luglio 2014
Matematica automobilistica: curve di Bézier e metodo della continuazione
E' interessante osservare come fino a una trentina di anni fa almeno l'industria automobilistica, almeno quella non italiana, aveva nella matematica una delle linee di ricerca fondamentali. In particolare ci sono due esempi cui sono incappato recentemente, le curve di Bézier e il metodo della continuazione.
Iniziamo con le prime: le curve di Bézier sono delle particolari curve parametriche sviluppate dall'ingegnere Pierre Bézier per la Renault da utilizzare per il design delle sue vetture. La matematica dietro queste curve prende le mosse dall'algoritmo sviluppato dal matematico francese Paul de Casteljau, che tra l'altro utilizzò questo metodo per conto, guarda un po' il caso, della Citroen. Oltre alle curve, però, si possono realizzare anche le superfici di Bézier, che insieme sono uno strumento importante nel mondo della computer graphics. Le curve vengono definite a paritre da due o più punti di controllo opportunamente ordinati. Detto $P_0$ il punto iniziale e $t \in [0,1]$ il parametro, le curve di Bézier possono essere definite o in modo ricorsivo \[B_{P_0} (t) = P_0\] \[B(t) = B_{P_0 P_1 \cdots P_n} (t) = (1-t)B_{P_0 P_1 \cdots P_{n-1}} (t) + t B_{P_0 P_1 \cdots P_n} (t)\] sia in maniera esplicita \[B (t) = \sum_{i=0}^n b_{in} (t) P_i\] dove $b_{in}$ sono i polinomi di Bernstein, così definiti \[b_{in} (t) = \binom{n}{i} t^i (1-t)^{n-i}\] per $i = 0, \cdots, n$.
Ovviamente si possono distinguere tra vari tipi di curve, partendo da quella lineare, ovvero un segmento tra due punti $P_0$, $P_1$, e quelle di ordine successivo (quadratica, tre punti; cubica, quattro punti; e così via)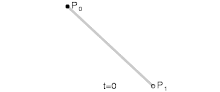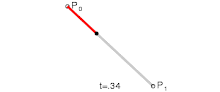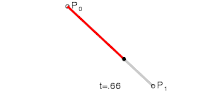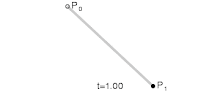

Iniziamo con le prime: le curve di Bézier sono delle particolari curve parametriche sviluppate dall'ingegnere Pierre Bézier per la Renault da utilizzare per il design delle sue vetture. La matematica dietro queste curve prende le mosse dall'algoritmo sviluppato dal matematico francese Paul de Casteljau, che tra l'altro utilizzò questo metodo per conto, guarda un po' il caso, della Citroen. Oltre alle curve, però, si possono realizzare anche le superfici di Bézier, che insieme sono uno strumento importante nel mondo della computer graphics. Le curve vengono definite a paritre da due o più punti di controllo opportunamente ordinati. Detto $P_0$ il punto iniziale e $t \in [0,1]$ il parametro, le curve di Bézier possono essere definite o in modo ricorsivo \[B_{P_0} (t) = P_0\] \[B(t) = B_{P_0 P_1 \cdots P_n} (t) = (1-t)B_{P_0 P_1 \cdots P_{n-1}} (t) + t B_{P_0 P_1 \cdots P_n} (t)\] sia in maniera esplicita \[B (t) = \sum_{i=0}^n b_{in} (t) P_i\] dove $b_{in}$ sono i polinomi di Bernstein, così definiti \[b_{in} (t) = \binom{n}{i} t^i (1-t)^{n-i}\] per $i = 0, \cdots, n$.
Ovviamente si possono distinguere tra vari tipi di curve, partendo da quella lineare, ovvero un segmento tra due punti $P_0$, $P_1$, e quelle di ordine successivo (quadratica, tre punti; cubica, quattro punti; e così via)


mercoledì 16 luglio 2014
Minimalia: istantanee da una camera a bolle
La settimana scorsa, su twitter, ho diffuso alcune immagini, foto scattate dalle pagine dal volume Letture da Le Scienze: Fisica delle particelle (un indice del volume), che raccoglieva alcuni articoli usciti sulla rivista italiana (e quindi anche su Scientific American). Poiché ognuna di quelle immagini fa inevitabilmente parte della storia della fisica, mi sembra sensato proporle raccolte insieme in un unico post molto più semplicemente raggiungibile di tanti piccoli... cinguettii.
 Rappresentazione di atomi, che poi mi sembra una bella immagine da usare e riusare per raccontare visivamente al meglio la struttura atomica, andando oltre l'atomo di Bohr. Provateci. Funziona. Soprattutto quando vedete lo stupore sui loro occhi quando gli dite: "L'atomo non funziona come un piccolo sistema solare"...
Rappresentazione di atomi, che poi mi sembra una bella immagine da usare e riusare per raccontare visivamente al meglio la struttura atomica, andando oltre l'atomo di Bohr. Provateci. Funziona. Soprattutto quando vedete lo stupore sui loro occhi quando gli dite: "L'atomo non funziona come un piccolo sistema solare"...
 Interazione dei neutrini con la materia dalla camera a bolle dell'Argonne National Laboratory. I neutrini, proposti teoricamente all'inizio degli anni trenta da Pauli e Fermi, vennero scoperti successivamente nel 1956. A proposito della teoria di Fermi c'è una curiosità: l'articolo venne originariamente proposto a Nature, che lo rigettò, pentendosi poi della decisione. Il lavoro uscì quindi in italiano, su Ricerca scientifica, e in tedesco, su Zeitschrift fur Physics, ma, secondo en.wiki, Nature tornò successivamente sui suoi passi, sembrerebbe il 16 gennaio del 1939. Cercando, però, l'unico articolo pertinente alla materia e vicino a quella data è Reactions Produced by Neutrons in Heavy Elements del 16 novembre 1940. D'altra parte è presente, sempre di Fermi, negli archivi della rivista anche Radioactivity Induced by Neutron Bombardment, che però è uscito lo stesso anno, il 1934, dell'articolo originale di Fermi, di cui è, ad ogni modo, disponibile una traduzione completa ad opera di Fred Wilson per l'American Journal of Physics del dicembre 1968 (pdf).
Interazione dei neutrini con la materia dalla camera a bolle dell'Argonne National Laboratory. I neutrini, proposti teoricamente all'inizio degli anni trenta da Pauli e Fermi, vennero scoperti successivamente nel 1956. A proposito della teoria di Fermi c'è una curiosità: l'articolo venne originariamente proposto a Nature, che lo rigettò, pentendosi poi della decisione. Il lavoro uscì quindi in italiano, su Ricerca scientifica, e in tedesco, su Zeitschrift fur Physics, ma, secondo en.wiki, Nature tornò successivamente sui suoi passi, sembrerebbe il 16 gennaio del 1939. Cercando, però, l'unico articolo pertinente alla materia e vicino a quella data è Reactions Produced by Neutrons in Heavy Elements del 16 novembre 1940. D'altra parte è presente, sempre di Fermi, negli archivi della rivista anche Radioactivity Induced by Neutron Bombardment, che però è uscito lo stesso anno, il 1934, dell'articolo originale di Fermi, di cui è, ad ogni modo, disponibile una traduzione completa ad opera di Fred Wilson per l'American Journal of Physics del dicembre 1968 (pdf).

Immagine estratta dall'edizione italiana di:
Weisskopf, V. (1968). The Three Spectroscopies Scientific American, 218 (5), 15-29 DOI: 10.1038/scientificamerican0568-15
Weisskopf, V. (1968). The Three Spectroscopies Scientific American, 218 (5), 15-29 DOI: 10.1038/scientificamerican0568-15

Immagine estratta dall'edizione italiana di:
Barish, B. (1973). Experiments with Neutrino Beams Scientific American, 229 (2), 30-38 DOI: 10.1038/scientificamerican0873-30
Barish, B. (1973). Experiments with Neutrino Beams Scientific American, 229 (2), 30-38 DOI: 10.1038/scientificamerican0873-30
lunedì 14 luglio 2014
Flash alla maniera di Ingmar Bergman
Jennifer Ouellette è uno dei blogger di Scientific American e ogni settimana propone una serie di link sulle novità riguardanti la fisica. Per la settimana del 12 luglio ci sono molte risorse interessanti, partendo da quelle dedicate al mondiale. Il lungo e ricco post si conclude con un video veramente interessante, così introdotto da Jennifer:

E ora il corto:

In onore dell'imminente serie televisiva The Flash, il filmmaker newyorkese Patrick Willems ha reimmaginato il supereroe velocista della DC Comics attraverso le lenti del leggendario regista svedese Ingmar Bergman.Da notare, in questo senso, i dubbi esistenziali dell'eroe ("Sono troppo veloce, o non sono veloce abbastanza?") o l'incontro con un teschio rivestito con il costume di Flash che rimandano, in particolare ai lettori trentenni, al Flash di Waid o a quello successivo di Morrison e Millar, gettando così una luce ancora più autorale su quella gestione, che si era concentrata essenzialmente sul terzo personaggio a rivestire il ruolo: Wally West.
E ora il corto:
La banda degli invisibili
La banda degli invisibili è una banda di divertenti signore e signori anziani, che trascorrono il loro tempo a chiacchierare, bisticciare, leggere il giornale e commentare le notizie alla tv. Ed è proprio ascoltando le notizie che hanno questa idea: rapire Silvio Berlusconi! Ebbene sì, è proprio quello che vogliono fare!
Per portare a termine l'operazione iniziano a 'fare palestra', ma in casa, perché con la loro pensione non possono permettersi certo una vera palestra. Tra disavventure, ossa rotte, un po' di Alzheimer ma tanta voglia di agire trovano così una nuova forma fisica, tanti amici disposti ad aiutarli ma soprattutto un rinnovato affetto e amicizia tra di loro.
Preparatevi a ridere (sin dalla seconda pagina), piangere anche un po', anche a riflettere su come un romanzo può essere molto vicino alla realtà, ma soprattutto si fa il tifo per questa divertentissima banda!
Per portare a termine l'operazione iniziano a 'fare palestra', ma in casa, perché con la loro pensione non possono permettersi certo una vera palestra. Tra disavventure, ossa rotte, un po' di Alzheimer ma tanta voglia di agire trovano così una nuova forma fisica, tanti amici disposti ad aiutarli ma soprattutto un rinnovato affetto e amicizia tra di loro.
Preparatevi a ridere (sin dalla seconda pagina), piangere anche un po', anche a riflettere su come un romanzo può essere molto vicino alla realtà, ma soprattutto si fa il tifo per questa divertentissima banda!
sabato 12 luglio 2014
I numeri primi e la ricerca delle fondamenta
Nel momento in cui affermiamo che un dato numero è primo, ovvero nel momento in cui affermiamo matematicamente che
All'interno di questo contesto, la definizione di numero primo è(1): Scritta così, perde sicuramente di chiarezza, ma ha il vantaggio di utilizzare esclusivamente un vocabolario fondamentale, lasciando quindi la sensazione che
Scritta così, perde sicuramente di chiarezza, ma ha il vantaggio di utilizzare esclusivamente un vocabolario fondamentale, lasciando quindi la sensazione che

$n$ è un numero primo
stiamo, in effetti, affermando che $n$ è un numero naturale divisibile solo per se stesso e per l'unità. Questa definizione può però essere ulteriormente ridotta come segue(1):
$n$ è un numero naturale e, presi comunque due numeri naturali $h$ e $k$, se $n$ è $h \cdot k$, allora $h$ o $k$ è 1.
E' chiaro, in questo caso, che il senso di riduzione per una definizione matematica va nella direzione del non utilizzare notazioni che necessitano di ulteriori definizioni, ovvero una ricerca delle basi fondamentali della matematica, di un linguaggio irriducibile che permetta di descriverla(1), possibilmente in maniera completa. In quest'ordine di pensieri, è evidente che la nuova definizione di numero primo non è ancora sufficientemente ridotta. Sono infatti molti gli elementi che possono essere ridotti ai loro minimi termini, partendo dal prodotto tra $h$ e $k$. Il modo usuale per arrivare alla definizione fondamentale di numero primo è passando attraverso la teoria degli insiemi, quella sviluppata da Georg Cantor, che diventa, quindi, il linguaggio fondamentale della matematica(2).All'interno di questo contesto, la definizione di numero primo è(1):

(...) tutta la matematica possa essere riscritta nel vocabolario della teoria degli insiemi.(1)Il problema è che si scoprì relativamente presto che la teoria degli insiemi è meno solida della matematica, che si fonda su di essa. La storia, infatti, è nota: nel 1901 Bertrand Russell scoprì il paradosso che porta il suo nome(1):
Esiste almeno un $y$ tale che per ogni $x$, $x \in y$ se e solo se non $x \in x$peccato che tale affermazione non sia dimostrabile. Da un punto di vista divulgativo, però, il paradosso è equivalente al famoso paradosso del barbiere (ispirato a un altro paradosso simile, ideato da Lewis Carroll), o, in una reinterpretazione vignettistica, il paradosso del postino(3):

domenica 6 luglio 2014
sabato 5 luglio 2014
Il pittore che visse due volte

Nel passato seguiamo le vicende di T.F. Reilly, giovane e talentuoso pittore londinese, probabilmente dallo stile impressionista, almeno se teniamo fede alle descrizioni dei quadri che ne fa Paling, in particolare di quello che muove tutto il romanzo, sia nel passato sia nel presente:
Autunno. Un giardino recintato da un muro grigio, verso fine pomeriggio. Un lampione (a gas, a guardare bene), spento. Colori tenui nel giardino d'autunno. La promessa dell'autunno nelle aiuole spoglie. La malinconia della vita.Reilly, in effetti, è interessato a catturare le impressioni del momento e a suscitarle, così, in chi guarda le sue tele. E per ripagare il suo amico barista Mountjoy, si lascia convincere da quest'ultimo prima a organizzare una mostra nel suo caffè, quindi a invitare presso il suo appartamento il famoso critico Gower, che era stato favorevolmente colpito proprio dal quadro d'autunno di cui sopra.
Il problema, per il giovane pittore, è che Gower, dopo la visita al suo studio, sparisce, e viene ripescato alcuni giorni dopo dal Tamigi, ovviamente morto. E nel frattempo il cane del pittore, Nimrod, ha riportato a casa del padrone il portafogli del critico, pieno di 150 sterline, e perso dal ricco mecenate mentre si preparava per una particolare transazione che lo aveva portato ai bordi del fiume londinese.
giovedì 3 luglio 2014
Diagonali prime

L'illustrazione della copertina [di Letture da Le Scienze: Verità e dimostrazione. Questioni di matematica], tratta dalla copertina del numero di marzo del 1964 di Scientific American disegnata da Joan Starwood, rappresenta un curioso comportamento dei numeri primi, cioé dei numeri interi che sono divisibili solo per se stessi e per l'unità, messo in luce per la prima volta da Stanislaw M. Ulam dei Los Alamos Scientific Laboratory. Ulam ha scoperto che se si scrivono i numeri naturali su carta quadrettata disponendoli secondo una spirale, i numeri primi tendono a disporsi lungo linee diagonali. Sulla copertina la spirale è indicata con una linea nera marcata, i numeri primi sono in rosso e le linee diagonali sono in verde.
mercoledì 2 luglio 2014
Pasta e geometria
La formula (come potete osservare in un estratto gratuito in pdf) è semplice: per ogni tipologia di pasta, si mostra la sua forma nel modo più essenziale possibile, utilizzando semplicemente il bianco e il nero, abbinando a una descrizione della pasta stessa e alcune ricette che si possono preparare con quella tipologia particolare.
L'interesse dei designer per la pasta, però, era già stato mostrato un paio di anni fa dall'architetto londinense George Legendre che in Pasta by Design ha mostrato le equazioni matematiche per descrivere una novantina di formati di pasta, tutti accompagnati dalle foto di Stefano Graziani: il libro esplora in profondità alcuni aspetti matematici della gastronomia molecolare(2).
Meccanicamente, la produzione di massa della pasta è un processo che dipende dalla pressione, dalla viscosità, da temperature precise, da differenziali di pressione e dal flusso dell'aria: tutti questi fattori determinano le proprietà materiali del prodotto - così come il suo valore di mercato.(2)Tralasciando tutti questi aspetti e utilizzando un modello parametrico delle superfici sviluppato dalla IJP, Lagrange esplora le proprietà geometriche della pasta, mostrando in questo modo le proprietà morfologiche uniche di ciascuno dei 92 tipi di pasta presi in esame.
In termini analitici, tutte le superfici parametriche matematiche si formano e si deformano come risposta diretta alle relazioni numeriche che intrattengono con il loro mezzo. All'osservatore che sa cosa cercare, la conformazione di una superficie parametrica esibisce le tracce di questi moti interni tanto marcatamente quanto la figura grassoccia di mezza età sussumerà le inflessioni più taglienti di un fisico giovanile.(1)
Alcune pagine tratte da The Geometry of pasta
Pasta by design su Brain Pickings
Foto e pagine da Pasta by design
(1) Legendre, G. (2011). IJP Explained: Parametric Mathematics in Practice Architectural Design, 81 (4), 44-53 DOI: 10.1002/ad.1267
(2) Legendre, G. (2011). Pasta by Design Architectural Design, 81 (4), 100-101 DOI: 10.1002/ad.1274
Architectural Design vol 81 (4) è disponibile completamente per la consultazione su Isuu
martedì 1 luglio 2014
Una (più o meno facile) dimostrazione del teorema di Pitagora

\[a^2 + b^2 = c^2\]
Che poi è una di quelle cose che quando scopri dici: ma perché non c'ho pensato prima? - via @MathUpdate
Iscriviti a:
Post (Atom)







