I Rompicapi di Alice: Le partizioni cicliche del Cappellaio Matto

Il party del Cappellaio Matto, variazione umoristica sui tea party vittoriani, è una delle scene più divertenti in Alice nel Paese delle Meraviglie, ed è anche un interessante concentrato di matematica, ora interpretabile come un letterale riferimento al tempo, ora come un riferimento alla matematica dei quaternioni.
I partecipanti alla festicciola, però, ovvero il Cappellaio, insieme con la Lepre Marzolina, il Ghiro e Alice, cambiano ogni tanto il loro posto intorno alla tavola circolare su cui sono poste le tazze.
Una possibile variazione sul testo carrolliano che il Cappellaio sembra abbia proposto ad Alice, nota appassionata di giochi matematici, è la seguente:

Partiamo con tante tazze quante sono le persone. Le tazze vengono sistemate in cerchio e ogni persona siede all'interno della propria tazza.
Alla fine del primo giro, si alzano tutti, una delle tazze viene rimossa, quindi tutti si siedono in un nuovo posto. Ogni tazza deve essere occupata da almeno una persona, così al secondo giro ci sarà una tazza con due persone all'interno. Dopo questo giro un'altra tazza scompare e alla fine, quando c'è giusto una tazza, nessuno sarà solo!⁽¹⁾

Ovviamente il gioco del Cappellaio riesce meglio se si utilizzano le tazze giganti di una giostra, a meno di non utilizzare i biscotti cambia dimensioni. Ad ogni modo, Alice, alla fine della descrizione del gioco, si chiede:

Se ci sono $n$ persone, quanti modi ci sono per sistemarle all'interno di $k$ tazze disposte in cerchio, assumendo, naturalmente, che tutte le persone sono uguali?⁽¹⁾

Nel caso di $n=5$, $k \leq 5$, si possono scrivere il numero di partizioni al variare di $k$ nella tabella seguente:

Alice osserva allora che la risposta alla sua domanda per gli $n$, $k$ dati è $7$, che è la somma delle due celle per $k = 3$, mentre $4$, che è il prodotto dei numeri delle partizioni per $k$ tazze, è il numero dei diversi percorsi attraverso le partizioni disponibili in ciascun giro.⁽¹⁾
Di fronte a questo risultato, il Cappellaio Matto, un po' perplesso, obietta che, secondo Martin Gardner, determinare una formula per contare le partizioni non è una procedura molto semplice, considerando anche che una delle formule più efficaci, la formula di Hardy-Ramanujan-Rademacher^{(3, 4, 5)}, piuttosto complicata, coinvolge tra gli altri, il pi greco, la radice quadrata, le radici complesse e le derivate delle funzioni iperboliche⁽²⁾.
Considerando il problema proposto da Alice come difficile, questa, per il Cappellaio, è un'ottima obiezione contro le argomentazioni della ragazzina, che però subito ribatte:

A volte è più semplice risolvere un problema più difficile e utilizzare quella soluzione per rispondere al problema più semplice.⁽¹⁾

Innanzitutto, dette le disposizioni cicliche delle tazze partizioni del Cappellaio, il problema si pone in questi termini: "Quante partizioni del Cappellaio ci sono per ogni intero $n$?"⁽¹⁾

1. Costruire il (possibile) simbolo ibrido per $b = 2^n -1$ e per $b = 2^n +1$
2. In ogni vettura ibrida per ogni simbolo ripetere la riga inferiore, se necessario, così che il valore $k$ per quella vettura sia $n$
3. Dalla riga inferiore delle vetture ricavare le partizioni del Cappellaio

Per capire come costruire il simbolo $b$, partiamo, per esempio, da 35. Prendiamo tutti i numeri dispari inferiori di $b/2$ e partiamo con il più piccolo, ovvero $1 = a_1$. Si esegue la sottrazione tra $b$ e $a_1$ e il risultato, 34 lo si divide per 2 fino a ottenere un numero dispari. Il risultato diventa il nuovo elemento della successione $a_i$, in questo caso $a_2 = 17$, mentre nella tabella del simbolo ibrido $b$ assegneremo al $k$ corrispondente con $a_1$ il numero di divisioni effettuate, in questo caso $k=1$.
Visto che mostrare è più semplice che spiegare, ecco lo sviluppo del metodo per $b = 35$:

La serie si interrompe con 3 poiché il risultato delle 5 divisioni per 2 produce come risultato 1, che è il numero di partenza.
Se osserviamo la prima riga, possiamo notare come non compaiono tutti i numeri dispari inferiori a $b/2$, così costruiamo una seconda vettura partendo da 5 e successivamente, sempre per lo stesso motivo, una terza vettura con l'ultimo numero dispari rimasto, 7. Alla fine si ottiene:

Le partizioni del Cappellaio Matto saranno proprio i numeri $k$ nella riga inferiore. Quasi, visto che bisogna ancora capire come agiscono i punti 2 e 3. Anche in questo caso usiamo un esempio, realizzando i calcoli per $n = 5$. In questo caso si dovranno produrre i simboli per $b = 2^5 -1$ e $b = 2^5 +1$:

Innanzitutto osserviamo come per tutte le vetture di $b=31$ la somma dei $k$ di ciascuna vettura è pari a 5. Quasi la stessa cosa avviene per le vetture di $b=33$ a parte l'ultima vettura, che ha valore $k=1$. In questo caso metteremo da parte un elenco di cinque 1, ottenendo alla fine le seguenti partizioni del Cappellaio Matto per $n=5$:

---

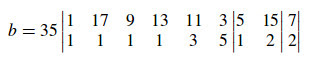
(1) Robert Bekes, Jean Pedersen, & Bin Shao (2012). Mad Tea Party Cyclic Partitions The College Mathematics Journal, 43 (1), 25-36 DOI: 10.4169/college.math.j.43.1.025
(2) Martin Gardner, Bulgarian solitaire and other seeminglv endless tasks, da The last recreation: hydras, eggs, and other mathematical mystifications
(3) Johansson, F. (2012). Efficient implementation of the Hardy–Ramanujan–Rademacher formula LMS Journal of Computation and Mathematics, 15, 341-359 DOI: 10.1112/S1461157012001088 (arXiv)
(4) Hardy, G., & Ramanujan, S. (1918). Asymptotic Formulaae in Combinatory Analysis Proceedings of the London Mathematical Society, s2-17 (1), 75-115 DOI: 10.1112/plms/s2-17.1.75 (pdf)
(5) Rademacher, H. (1938). On the Partition Function p(n) Proceedings of the London Mathematical Society, s2-43 (4), 241-254 DOI: 10.1112/plms/s2-43.4.241