In una delle due prime, però, non contento, ha completato (se così si può dire) la lezione con il metodo della parallasse, e qui la grande coincidenza: proprio questa settimana mi sono dedicato ad approfondire tale metodo e più in generale la misurazione delle distanze stellari.
Adatterò un po', per questo post, quanto scritto, come potete immaginare, per le Olimpiadi dell'Astronomia. Iniziamo:
Misurare la distanza delle stelle dalla Terra non è una operazione semplice come, ad esempio, misurarne la luminosità o la declinazione. Sono stati, allora, sviluppati vari metodi di misurazione, di cui il più noto di tutti è quello della parallasse, che può essere utilizzato anche per misurare la distanza degli oggetti sulla Terra, a patto di conoscere più o meno precisamente alcune distanze.
Prima di capire in pratica come funziona il metodo della parallasse, proviamo a fare uno sforzo di immaginazione: supponiamo di disegnare un triangolo che ha per vertici la Terra, il Sole e la stella di cui vogliamo misurare la distanza; l'angolo di parallasse sarà, allora, l'angolo del vertice corrispondente alla stella.
Per misurare questo angolo si deve, allora, misurare due volte la posizione della stella rispetto alle stelle dello sfondo (che hanno una parallasse pressocché nulla) con la Terra che si trova in due posizioni differenti della sua orbita, possibilmente due posizioni una opposta all'altra, in modo tale che questa distanza sia circa il diametro dell'orbita (300 milioni di km)(3). Ciascuna delle due misure è, in realtà, una fotografia della porzione di cielo in cui si trova la stella: sovrapponendo le due foto gli astronomi sono in grado di determinare l'angolo di parallasse(4). Il metodo della parallasse, però, è efficace solo fino a un centinaio di parsec(5), o qualcosa di meno, e quindi è stato necessario sviluppare delle tecniche differenti. Tra queste altre il più noto è certamente il metodo delle cefeidi.
Questa è un tipo di stella la cui luminosità varia periodicamente, secondo un grafico di questo tipo: Le potenzialità delle cefeidi per determinare le distanze delle altre stelle furono evidenti quando Henrietta Swan Leavitt, studiando le cefeidi della Grande Nube di Magellano(1), si accorse come il periodo delle stelle fosse legato con la luminosità. Questa osservazione, successivamente confermata dalla stessa Leavitt(2), può essere espressa nella seguente forma matematica: \[M = A + B \cdot \log T\] dove $T$ è il periodo, $M$ la magnitudine della cefeide, $A$, $B$ due parametri da determinare a partire dai dati.
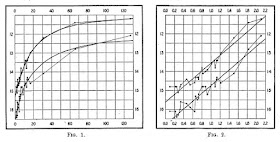
Nel grafico in figura 1, sull'asse delle ascisse ci sono i periodi, su quello delle ordinate le magnitudini; in figura 2 sull'asse delle ascisse ci sono i logaritmi dei periodi
la natura della relazione periodo-luminosità nelle varie bande passanti, l'impatto della metallicità sia sul punto-zero sia sulla pendenza di tali relazioni, e gli effetti di combinazione fotometrica e una legge di estinzione che cambia sulle distanze delle cefeidi.Un altro problema interessante è che le cefeidi sembrano perdere massa, con una conseguente produzione di polvere stellare che ne offuscherebbe la luminosità, rendendo di fatto la stima della distanza delle cefeidi errata.
Risolvere questi problemi non è solo una questione legata alla determinazione precisa delle distanze degli oggetti luminosi nell'universo, ma anche legata più in generale alla determinazione delle caratteristiche del nostro universo, costante di Hubble su tutte.
(1) Leavitt, Henrietta S. (1908). "1777 variables in the Magellanic Clouds". Annals of Harvard College Observatory 60: 87.
(2) Leavitt, Henrietta S.; Pickering, Edward C. (1912). "Periods of 25 Variable Stars in the Small Magellanic Cloud". Harvard College Observatory Circular 173: 1.
(3) Come si fa a misurare la distanza delle stelle
(4) Il metodo della parallasse
(5) Il parsec è una unità di misura astronomica utilizzata dagli astronomi dopo l'introduzione del metodo della parallasse ed equivale a circa 3,26 anni luce.



Intanto complimenti per l'articolo davvero interessante.
RispondiEliminaRiguardo all'usare il laboratorio come aula per le lezioni e avere un tecnico di laboratorio è un sogno che non ho mai potuto concretizzare. Per noi già è molto se il laboratorio lo vediamo 2 o 3 volte l'anno. Sarei curioso di sapere se i ragazzi si sono chiesti anche loro il perché il laboratorio venga usato come aula, ma sono quasi certo che non si sono fatti tante domande, hanno goduto della cosa e basta.
Peccato constatare come la scuola, in generale in grosse difficoltà, crei comunque differenze sostanziali a seconda se si ha la fortuna di vivere in un posto o avere docenti con i cosiddetti o meno.
Anche l'istruzione è soggetta alla fortuna! Non dovrebbe essere così però.
Un saluto
Marco