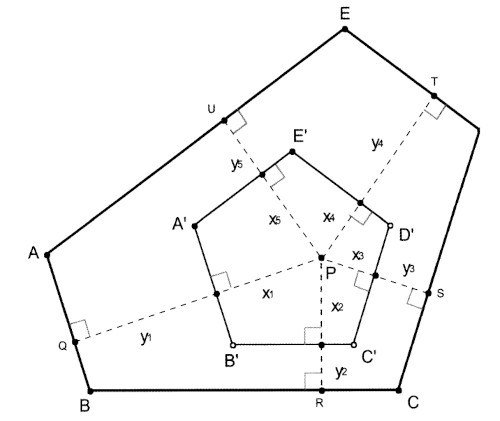
Un coccodrillo matematico vive nel delta dell'Okavango vive in una regione paludosa a forma di pentagono irregolare equiangolare (ovvero con tutti gli angoli uguali). Poiché il coccodrillo cattura la preda un numero uguale di volte su ciascuna delle cinque sponde, vuole nasconderla nel punto dove la somma delle cinque distanze dalle rive è minima. Dov'è questo punto ottimale?Il fatto che il pentagono non sia regolare non deve trarre in inganno: anche nel caso di un pentagono semplicemente equiangolare è possibile trovare una soluzione. In particolare partiamo da un pentagono regolare: secondo il teorema di Viviani, la somma delle distanze di un qualunque punto interno al pentagono da ciascun lato è costante: chiamiamo questa somma $X$.
Disegnamo un pentagono regolare all'interno del pentagono irregolare. Poiché gli angoli del pentagono regolare sono uguali agli angoli del pentagono equiangolare, allora i lati esterni sono paralleli ai lati interni, quindi la somma delle distanze tra i lati interni ed esterni è costante, quale che sia la posizione del pentagono interno. Chiamiamo questa somma $Y$.
Quindi se prendiamo un qualsiasi punto $P$ all'interno del pentagono regolare, la somma delle distanze dai lati del pentagono equiangolare dal punto scelto sarà $X + Y$, che è costante poiché sia $X$ sia $Y$ sono costanti.

Nessun commento:
Posta un commento