Un fatto curioso sui semicerchi

Dopo un periodo (che definirei terribile) finanche troppo lungo in cui ho passato a vedere ogni giorno i video di MasterChef Italia, sono finalmente uscito dal tunnel e ho ripreso possesso di YouTube, riuscendo a riportare in home page i miei video preferiti, quelli legati al metal in varie declinazioni, alla musica classica e alla scienza. In particolare il tubo mi ha consigliato un video particolare, A Curious Fact About Semicircles e mi è venuto in mente che avrei potuto usarlo per un nuovo post della serie senza parole. Poi mi sono reso cnto che mi servivano due immagini, e allora ho realizzato un'infografica matematica (qui il pdf e per i più curiosi ecco il LaTeX). Ovviamente qui sotto vi ho spezzato l'infografica nelle due immagini principali, ognuna delle quali corredata delle sue equazioni. Rispetto al video cambia la dimostrazione della prima immagine, dove sfrutto il teorema delle corde.
Alla fine ho scritto troppo, ma mi sembrava giusto metterci un po' di contesto. Il resto lo lascio alle immagini e alle formule:

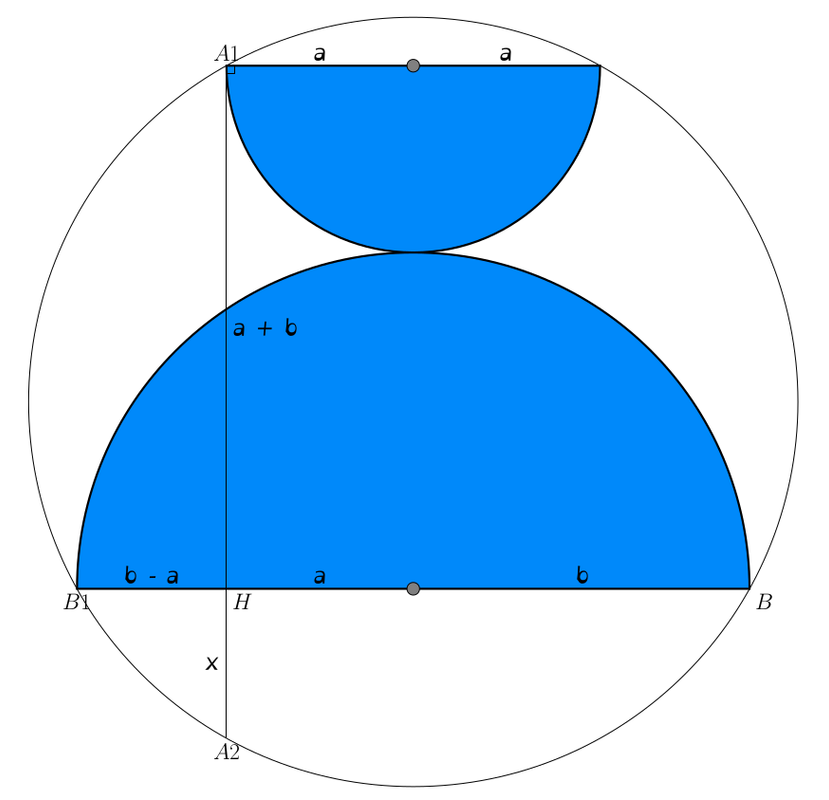
\[A_1H : HB = B_1H : HA2\] \[A_1H = a+b = HB \Rightarrow b-a = B_1H = HA_2 = x\]

\[(2a)^2 + (2b)^2 = (2r)^2 \Rightarrow a^2 + b^2 = r^2\] \[A_a = \frac{1}{2} \pi a^2, \qquad A_b = \frac{1}{2} \pi b^2\] \[A_c = \frac{1}{2} \pi r^2\] \[A_a + A_b = \frac{1}{2} \pi (a^2 + b^2) = \frac{1}{2} \pi r^2 = \frac{1}{2} A_c, \, \forall a, b \in R\]