Mentre approfondivo questa teoria, imparai la mia prima e unica parola in sanscrito: yamátárájahánsalagám.Questa parola non aveva alcun significato particolare, ma aveva un uso più utilitaristico: serviva ai batteristi indiani per ricordare un particolare ritmo. D'altra parte oltre quelle dieci sillabe c'è di più, per parafrasare una nota canzone di alcuni decenni fa. Come ricorda Perle a Stein, pronunciare la parola sanscrita di cui sopra vuol dire pronunciare tutte le possibili terzine di battiti brevi e lunghi.
Le prime tre sillabe, ya má tá, hanno il ritmo breve, lungo, lungo. Dal secondo al quarto sono má tá rá: lungo, lungo, lungo. Poi hai tá rá já: lungo, lungo, breve. Poi ci sono rá ja bhá: lungo, breve, lungo. E così via.E questo, alle orecchie di Stein, aveva un che di matematicamente affascinante: era l'inizio di una sequenza.
Il matematico, infatti, associò alla sillaba breve il numero 0 e a quella lunga il numero 1, ottenendo 0111010001.
La cosa che saltò subito all'occhio di Stein fu il fatto che le prime due e le ultime due cifre di questo numero binario fossero identiche. Questo voleva dire che era possibile chiudere il numero in una sorta di ruota e rappresentarlo non con 10 ma con 8 cifre. Aveva ottenuto una struttura che chiamò "ruota della memoria" (memory wheel).


Stein, prima di affrontare le quartine, prova con i distici, ovvero con le quattro combinazioni possibili di 0 e 1. Ottiene 00110, la cui prima cifra coincide con l'ultima. Notiamo che il numero di cifre uguali nella parola uroborica è inferiore di una cifra rispetto alla lunghezza delle combinazioni di cui è costituita. Quet'ultima parola uroborica è, in effetti, costituita da distici, ovvero coppie di cifre, per cui il collegamento tra testa e coda è dato solo da una cifra. Allo stesso modo la parola uroborica dei batteristi indiani è costituita da terzine di cifre, e di conseguenza sono le prime due cifre a coincidere con le ultime due.
Torniamo, però, alla ricerca della parola uroborica generata da tutte le quartine possibili. Queste, una volta scritte tutte, si rivelano essere 16 (e quindi si può prevedere che la parola uroborica deve essere costituita da 19 cifre: 16 come le quartine generatrici + 3 che sono le cifre che collegano inizio e fine). E la parola uroborica generata dalle 16 quartine senza alcuna ripetizine risulta essere alla fine 1111000010100110111.

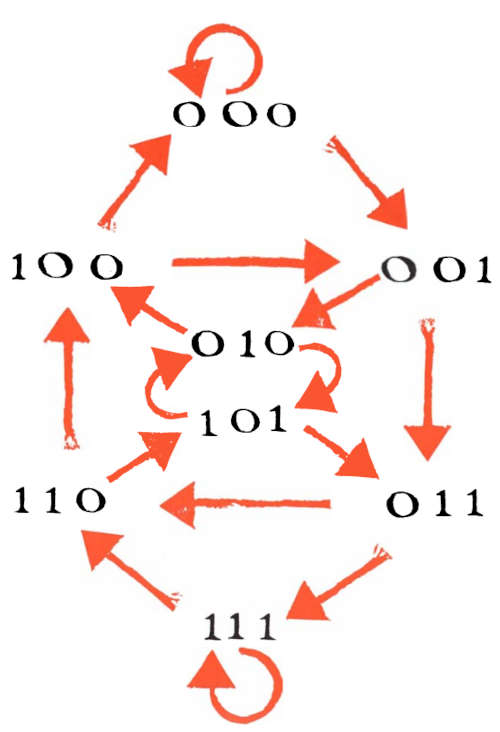
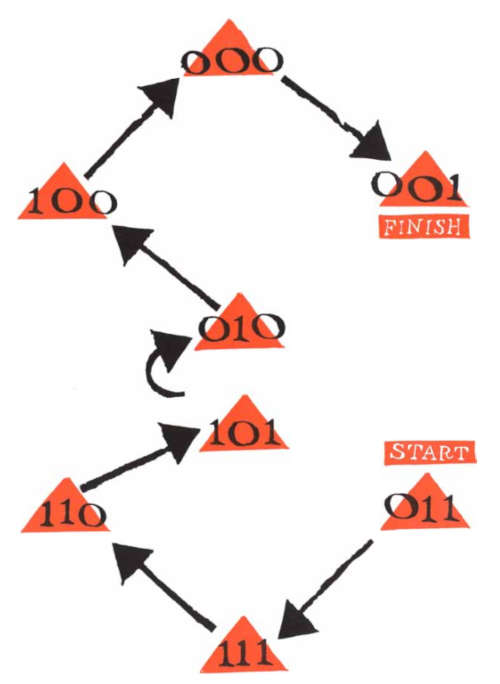
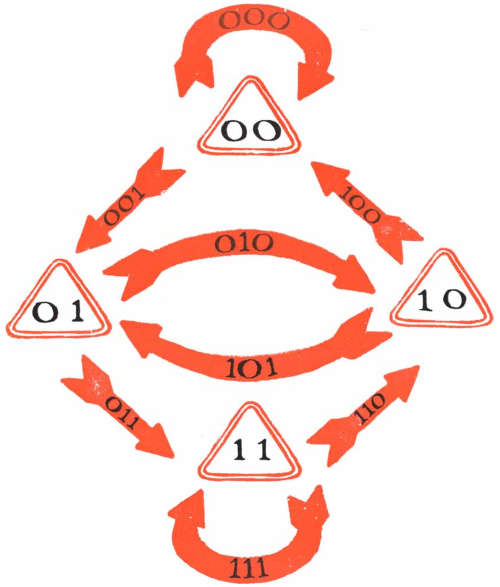
Prendiamo la terzina 011. Questa rappresenta la strada che porta dalla città 01 alla città 11. In questo modo ecco spuntare la mappa con tutte le possibili strade che collegano le quattro città 00, 01, 10, 11:
E questa è la storia di come una parola ritmica usata dai batteristi indiani abbia portato in un fantastico viaggio di esplorazione un matematico statunitense fino alla fredda Europa sulle soglie della matematica dei nodi.
- In effetti Stein la chiama semplicemente parola, ma l'aggiunta dell'aggettivo uroborica, ispirata dal capitolo in cui Ian Stewart nel suo La piccola bottega delle curiosità matematiche tratta brevemente della questione, secondo me identifica meglio la proprietà che deve avere la parola in questione: un certo numero di cifre finali identiche allo stesso numero di cifre iniziali. ↩
- Good, I. J. (1946). Normal recurring decimals. Journal of the London Mathematical Society, 1(3), 167-169. doi:10.1112/jlms/s1-21.3.167 ↩
- Stein, S. K. (1961). The mathematician as an explorer. Scientific American, 204(5), 148-161. doi:10.1038/scientificamerican0561-148 (jstor) ↩

Nessun commento:
Posta un commento