Nel primo caso la formula dell'accelerazione di gravità è data da \[g = \frac{4}{3} \pi \rho G r\] dove \(M\) è la massa dell'oggetto, \(\rho\) la sua densità, \(G\) la costante di gravitazione universale, \(r\) la distanza dal centro.
In questo caso l'accelerazione di gravità varia secondo una legge lineare (come una retta).
Se invece la distanza è superiore al raggio dell'oggetto, allora la formula risulta quella classica \[g = \frac{G M}{r^2}\] che poi la prima formula è ricavata dalla seconda a partire dalla formula della densità, presa come uniforme.
In questo secondo caso l'accelerazione di gravità varia come l'inverso del quadrato della distanza.
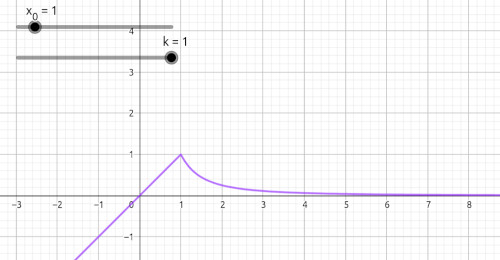
I calcoli, però, li ho realizzati avendo in mente di realizzare qualcosa di interattivo sulla faccenda. In un primo tentativo, che non vi linko, la cosa non era agilmente visualizzabile. A quel punto ho preso due funzioni diverse \[f(x) = kx, x < x_0\] \[g(x) = \frac{1}{x^2}, x \geq x_0\] e messo tutto su GeoGebra, dove i parametri \(k\) e \(x_0\) sono diventati due slider. In questo modo è molto più semplice visualizzare l'andamento della gravità in uno spazio ridotto come quello di una applet GeoGebra rispetto all'uso delle costanti vere e proprie e delle masse realmente presenti nell'universo.
Come potrete notare, \(f(x)\) modellizza la gravità dentro l'oggetto, \(g(x)\) la gravità all'esterno. L'applet potete sperimentarla sul sito di GeoGebra oppure scaricare il file sul mio repository su gitea.

Nessun commento:
Posta un commento