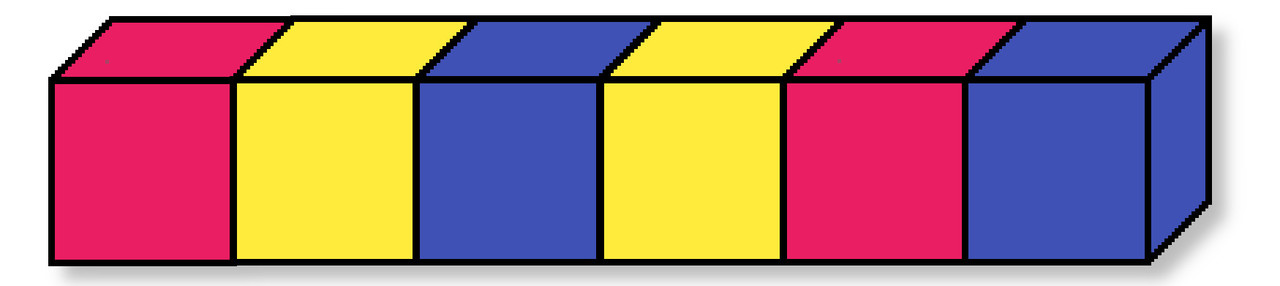
Il figlio del matematico scozzese Dudley Langford stava giocando con alcuni cubi colorati. A un certo punto il bambino si trovò con una combinazione particolare di sei cubi costituita da due di colore giallo, due di colore blu e due di colore rosso. La combinazione era quella qui sotto:

In effetti più che una generalizzazione si può parlare del così detto problema di Langford (o degli accoppiamenti di Langford), ovvero se esistono disposizioni simili a quelle di cui sopra per un numero di coppie arbitrario.
Il problema venne proposto da Langford nel 1958 nella pagina dei problemi della Mathematical Gazette e già l'anno dopo Roy Davies dimostrò che esistevano soluzioni al problema di Langford se e solo se \(n \equiv 0, 3 (\mod 4)\).
Per ciascun \(n\) è possibile calcolare il numero di soluzioni al problema di Langford (ovvero di disposizioni per ciascun numero di coppie di cubi distinti), ottenendo che non ci sono soluzioni per 1, 2, 5 e 6 coppie, mentre per 7 coppie esistono ben 26 soluzioni! Ovviamente esiste una sequenza che trovate su The On-Line Encyclopedia of Integer Sequences.
Per quel che mi riguarda, non mi resta che invitarvi a scoprire la soluzione per 4 coppie, magari usando, come ho fatto io, le carte corrispondenti, napoletane o francesi a vostro gusto!
Cubi colorati realizzati con pixilart.com

Nessun commento:
Posta un commento