La principale difficoltà nel coprire la superficie di una sfera con dei triangoli è che la superficie che vogliamo ricoprire ha una curvatura, mentre la figura che vogliamo utilizzare è piatta. QUesto vuol dire che se vogliamo utilizzare un triangolo o un qualsiasi altro poligono regolare per ricoprire la superficie di una sfera, questa figura non sarà mai identica a quella corrispondente nella usuale geometria euclidea.
Per capire la differenza, partiamo da un poligono regolare di \(n\) lati. Esso potrà essere suddiviso in altrettanti triangoli, che divideranno l'angolo al centro secondo la regola: \[\frac{2\pi}{n}\] Supponiamo, ora, che in uno dei vertici del poligono si incontrino \(k\) poligoni regolari, quindi l'angolo giro intorno a quel vertice sarà diviso in \(k\) angoli della seguente ampiezza: \[\frac{2\pi}{k}\] In caso di geometria euclidea la somma di questi due angoli coinciderebbe con l'angolo piatto, ma in una geometria sferica vale la relazione: \[\pi \left ( \frac{2}{n} + \frac{2}{k} \right ) > \pi\] che diventa \[k \le \frac{2n}{n-2}\] Ovviamente i casi possibili sono per \(n \ge 3\). Se per esempio prendiamo \(n=3\), \(k\) potrà assumere i valori 1, 2, 3, 4, 5. In particolare per \(k=3\) avremo un tetraedro, per \(k = 4\) un ottaedro e per \(k = 5\) un icosaedro, ovvero cinque possibilità differenti di piastrellare senza "buchi" la superficie di una sfera utilizzando una figura dotata di tre lati e tre vertici, che solo per cortesia possiamo chiamare triangolo!
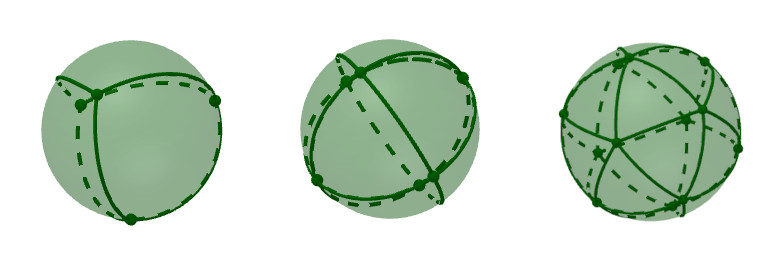
I tre solidi platonici "sferici" con facce "triangolari" - Immagini e parte delle formule da Tiling the sphere by Tevian Dray
Ultima curiosità: possiamo calcolare il numero di facce di questi pseudo solidi sferici utilizzando la formula \[p = \frac{4k}{2n+2k-kn}\]
Attenzione! In effetti c'è una possibilità di utilizzare triangoli veri e propri se ci accontentiamo di un'approssimazione ragionevole, diciamo entro l'errore che commettiamo nella misura degli angoli. Per avere un'idea, supponiamo di avere un triangolo isoscele di lati \(l\) e base \(a\). Detti \(\alpha\) l'angolo al vertice e \(\beta\) gli angoli alla base, la lunghezza della base sarà data da: \[a = \frac{\sin \alpha}{\sin \beta} l\] Nel caso del triangolo equilatero che vogliamo utilizzare per piastrellare la sfera, la lunghezza del lato \(t\) di questo triangolo sarebbe data da una relazione simile a questa: \[t = \frac{\sin \alpha}{\sin \beta} r\] dove \(r\) è il raggio della sfera, mentre \(\alpha\) e \(beta\) gli angoli del triangolo isoscele costituito unendo il lato del triangolo con il centro della sfera. Affinché il nostro triangolo sia approssimativamente piatto (ovvero tale per cui non ci accorgeremmo della sua curvatura), devo poter approssimare il seno dell'angolo al vertice \(\alpha\) con il valore dell'angolo stesso. O, in altre parole, il lato del triangolo che voglio utilizzare per piastrellare la sfera deve essere trascurabile rispetto al raggio della sfera.

Nessun commento:
Posta un commento