Vi scrivo questo perché, giusto ieri, mi è arrivato in timeline su twitter un estratto di una partita del campionato mondiale indoor di bocce (a quanto sembra quello dell'anno scorso, svoltosi prima dell'esplosione della pandemia in Europa). Nell'estratto del video si vede un colpo a effetto particolarmente preciso realizzato da Nick Brett, che come si vede da un video più lungo si è successivamente ripetuto con un tiro ancora più spettacolare, se possibile: In realtà nelle bocce i tiri a effetto sono abbastanza comuni nel corso delle partite, ma ciò che è interessante andare a esaminare è la traiettoria delle bocce stesse, che non è parabolica. Il motivo è dovuto a quali grandezze fisiche influiscono sulla traiettoria stessa.
Innanzitutto abbiamo l'equazione del moto lineare della palla (che poi è la più semplice e quindi ve la metto): \[v = v_0 - \mu g t\] dove $v_0$ è la velocità iniziale, $\mu$ la costante di attrito dinamico, $g$ l'accelerazione di gravità, $t$ il tempo.
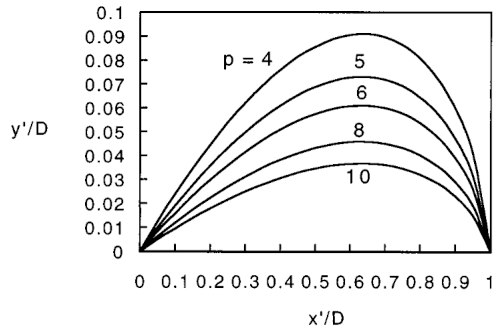
La sfera che viene usata nelle bocce, però, non è un punto materiale ma, appunto, una sfera e quindi è soggetta a una rotazione intorno al proprio asse. Questo vuol dire che bisogna tenere conto anche del momento angolare della sfera e dalla velocità di rotazione della sfera stessa. Introducendo anche questo secondo moto, la traiettoria della boccia (che viene ricavata utilizzando l'operazione di integrazione) quando il giocatore gli fornisce un effetto particolare non è per niente parabolica, ma risulta leggermente più complicata (sono coinvolte le funzioni trigonometriche, giusto per essere un po' più specifici).
Utilizzando il software Tracker ho provato a mettere in evidenza la traiettoria della boccia in due momenti chiave e provato a tracciare il grafico della traiettoria nel piano $x-y$. La forma dei due grafici non sembra esattamente identica al grafico messo prima, ma immagino che il problema sia dovuto all'effetto di prospettiva della telecamera. Ad ogni modo qui sotto un video che sintetizza la cosa e mostra traiettorie e grafici: In chiusura, la cosa bella che vorrei rilevare è che le bocce sono sport paraolimpico!
Cross, R. (1998). The trajectory of a ball in lawn bowls. American Journal of Physics, 66(8), 735-738. doi:10.1119/1.19028
All'articolo di ricerca che ha fatto da base a questo articoletto ne aggiungo un altro correlato che potrebbe essere interessante:
Medwell, P. R., Brooks, L. A., & Medwell, B. S. (2011). Analysis of the Lawn Bowl Trajectory as a teaching tool for Sports Engineering: development of a graphical user-interface. Procedia Engineering, 13, 531-537. doi:10.1016/j.proeng.2011.05.126

Nessun commento:
Posta un commento