Le grandi domande della vita: Soluzioni grafiche

Mi sono imbattuto in due domande piuttosto analoghe, una relativa alla soluzione di questa equazione: \[5^x - 3^x = 16\] e una seconda relativa a quest'altra equazione: \[x^2 = 2^x\] In entrambi i casi non esiste un modo algebrico per trovare la soluzione, ma grafico.
Nel primo caso, usando Wolfram Alpha, si ottiene come soluzione 2. Il secondo caso, invece, è leggermente più semplice, visto che almeno due delle tre soluzioni sono facili da determinare con un ragionamento abbastanza semplice.
La prima soluzione facile nella seconda equazione è ancora una volta 2. Per la seconda soluzione basta pensare alla prima delle potenze non banali di 2, il 4. In questo caso avremmo \[\left ( 2^2 \right )^2 = 2^{\left ( 2^2 \right )}\] Ovvero 16 da ambo i lati.
Il giochino, però, risulta vero solo per $2^2$, quindi per la terza soluzione siamo comunque costretti a optare per il metodo grafico.

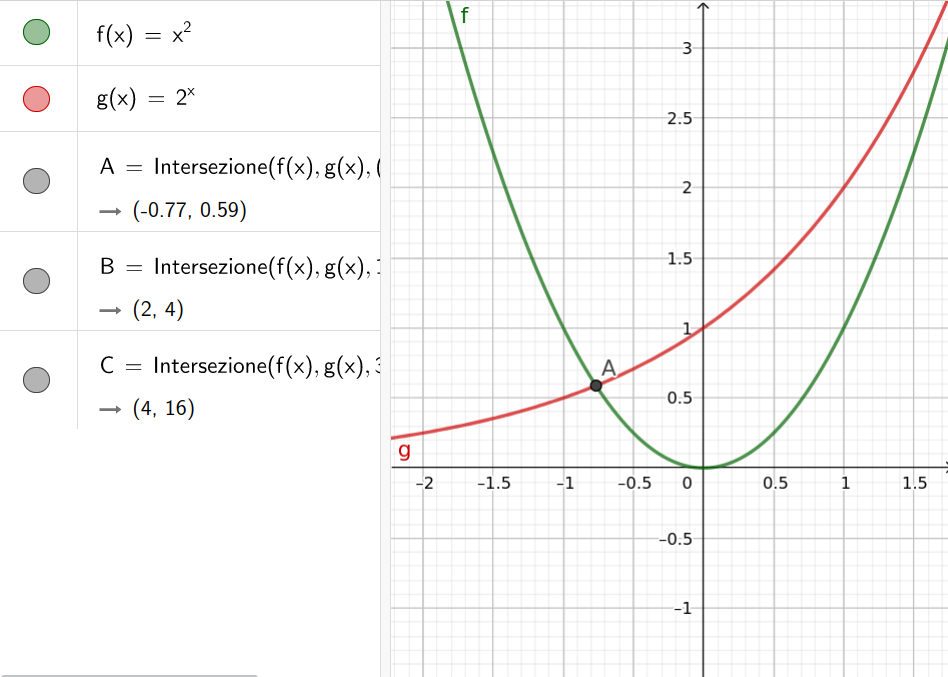
Grafico realizzato con GeoGebra

Addendum

La prima equazione mi ha spinto a fare una ricerca sulla generalizzazione dell'espressione \[x^2 - y^2 = (x-y)(x+y)\] Conosciamo tutti la formula per la scomposizione della differenza dei cubi (ce la insegnano a scuola insieme con la formula per la somma dei cubi): \[x^3 - y^3 = (x-y)(x^2+xy+y^2)\] Questa cosa qui, però, ovvero la scomposizione della differenza di potenze, può essere generalizzata in questo modo: \[x^n - y^n = (x-y)(x^{n-1} + x^{n-2}y + \cdots + xy^{n-2} + y^{n-1})\] Ovviamente c'è anche una dimostrazione che però non vi metto qui sotto.