Leonardo da Vinci è uno degli italiani più noti di tutti i tempi. Aveva molti interessi, dall'architettura, alla pittura, all'ingegneria, alla matematica e altro ancora. In particolare nel campo della matematica, come abbiamo visto in altra occasione, probabilmente ha inserito un bel po' di matematica all'interno del suo
uomo vitruviano. Però ha anche realizzato una serie di disegni geometrici per uno dei trattati più famosi dell'antichità, il
De divina ratio del 1509 di
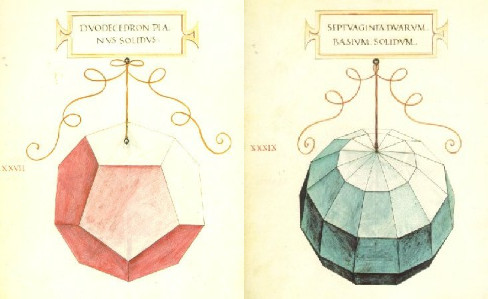
Luca Pacioli, in particolare una serie di poliedri regolari, in particolare dei
solidi platonici (tetraedro, cubo, ottaedro, dodecaedro e icosaedro).
La definizione formale dei solidi platonici è poliedri convessi regolari le cui facce sono costituite da poligoni regolari congruenti, ovvero esattamente sovrapponibili, e con tutti gli spigoli e i vertici equivalenti. Questo vuol dire che gli angoli solidi ai vertici sono tutti uguali. Ne consegue che anche i suoi angoloidi hanno la stessa ampiezza.
Di poliedri regolari così fatti ne esistono solo cinque, non di più, come dimostrato da
Euclide nei suoi
Elementi. I motivi sono essenzialmente quattro.
Innanzitutto in ogni vertice devono convergere almeno tre facce. Inoltre, per evitare che l'angoloide formato risulti piatto, la somma degli angoli che convergono nei vertici deve essere minore di 360°. Questo vuol dire che gli angoli al vertice devono essere al massimo pari a 120° = 360°/3. Questo vuol dire che gli unici poligoni che possono formare dei solidi platonici sono triangolo, quadrato e pentagono. Il che porta ai cinque solidi regolari di cui sopra. E nulla di più.
Altri dei solidi platonici disegnati da Leonardo li potete trovare su
Life Through A Mathematician's Eyes e su
Leonardo da Vinci's Polyhedra.

Nessun commento:
Posta un commento