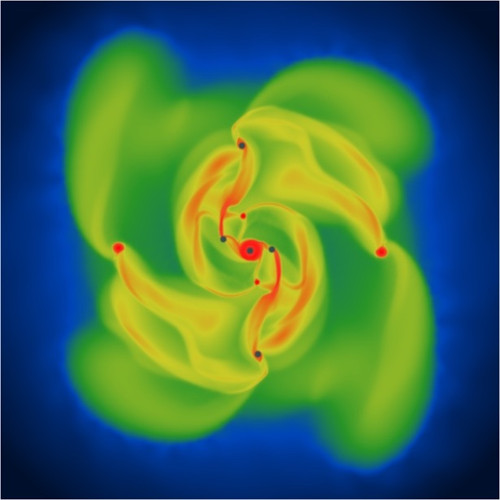
La faccenda è abbastanza semplice: un paio di ricercatori del Jeremiah Horrocks Institute presso la University of Central Lancashire hanno voluto testare, con opportuna simulazione al computer, il modello del disco di instabilità, secondo cui i proto-pianeti, ovvero quegli aggregati di materia che vengono considerati "embioni" di pianeti, destinati a crescere assimilando polveri e rocce spaziali, si formano in tempi relativamente brevi all'interno del disco di accrescimento intorno a stelle giovani. L'obiettivo era quindi quello di determinare le proprietà dei pianeti, confrontarsi con le osservazioni e comprendere il processo di formazione dei pianeti, in particolare dei giganti gassosi.
Lo studio della forma dei pianeti in formazione, però, è stato un bonus in qualche modo imprevisto, una curiosità che i due ricercatori hanno verificato e che li ha in qualche modo stupidi. A tal proposito, come si legge nel comunicato stampa, Dimitris Stamatellos, uno dei due autori del lavoro, per ora uscito solo come preprint, ha affermato:
Abbiamo sempre assunto che fossero sferici. Siamo stati molto stupiti che si siano rivelati degli sferodi oblati, molto simili agli smarties!Ed è a questo punto che colgo l'occasione per infilarci un po' di matematica!
Uno sferoide oblato, infatti, è un particolare ellissoide, dove per ellissoide si intende l'equivalente tridimensionale di un ellisse, come evidente sin dalla sua formula matematica: \[\frac{x^2}{a} + \frac{y^2}{b} + \frac{z^2}{c} = 1\] Nello specifico si ha un ellisside oblato quando \(a = b > c\), quindi in parole più semplici una sfera schiacciata ai poli. Come la Terra. Solo che, come nel caso dei proto-pianeti, lo schiacciamento dovuto a \(c\) è tale per cui la forma è più simile a quella di un disco un po' cicciotto al centro. O uno smarties, come detto in termini un po' più pop da Stamatellos.
Poi, da qui, il passaggio a una simmetria sferica (o quasi sferica) avviene proprio grazie all'aumento della massa e alla conseguente riduzione della velocità di rotazione.

Nessun commento:
Posta un commento