Nel corso delle sue peregrinazioni, Didone arrivò sulle coste dell'attuale Tunisia, nei pressi di Tunisi. Il posto le piacque, così chiese al re di quelle terre, Iarba, il permesso per edificare una città. Il suo obiettivo era quello di eguagliare, se non addirittura superare la potenza di Tiro. Iarba, però, con un qual certo scherno, le concesse tanto terreno "quanto ne poteva contenere una pelle di bue".
Didone, però, ragionò in termini matematici: strappò a strisce sottilissime la pelle di bue e creò una semicirconferenza, in modo tale da delimitare un terreno di fronte alla costa, visto che l'accesso al mare poteva fare la differenza negli scambi commerciali. Non è detto che il mito non abbia un qualche elemento di verità, visto che l'antico nome di Cartagine, Birsa, significa "rocca" in fenicio e "pelle di bue" in greco!
Il problema che dovette risolvere Didone, però, è un problema isoperimetrico o di isoperimetria, che in termini matematici viene rappresentato dalla seguente disuguaglianza \[4 \pi A \leq P^2\] dove \(A\) è l'are a e \(P\) il perimetro della curva. E questa disuguaglianza diventa un'uguaglianza solo quando la curva diventa una circonferenza, poiché la sua area è pari a \(A = 2\pi r^2\) e il perimetro \(P = 2 \pi r\).
Per arrivare a questa rappresentazione relativamente "semplice" del problema, però, ci sono voluti diversi secoli.
Triangoli e cerchi
Il primo matematico ad affrontare tale problema fu Zenodoro, all'incirca in un qualche punto nel secondo secolo a.C. Del suo trattato Sulle figure isoperimetriche siamo venuti a conoscenza grazie agli scritti di Teone di Alessandria e di Pappo, anch'egli di Alessandria.
In particolare Teone scrive:
Allo stesso modo, poiché la più grande tra le figure che hanno stesso perimetro è quella che ha più angoli, il cerchio è la più grande tra le figure piane e la sfera tra i solidi.Secondo Teone, Zenodoro prima dimostra che "se vi sono due triangoli sulla stessa base e con lo stesso perimetro, uno isoscele e l'altro scaleno, il triangolo isoscele ha area maggiore", e poi "dati due triangoli isosceli non simili tra loro, se [si costruiscono] sulle stesse basi due triangoli simili tra loro tali che la somma dei loro perimetri sia uguale alla somma dei perimetri dei primi due triangoli, allora la somma delle aree dei triangoli simili è maggiore della somma delle aree dei triangoli non simili" e da qui costruisce, o dovrebbe costruire, un metodo molto simile a quello adottato da Archimede per il calcolo del pi greco. Il condizionale però è d'obbligo, perché di come Zenodoro avrebbe portato a termine la dimostrazione non se ne ha traccia.
In effetti, però, Pappo fa qualcosa in più e dimostra il risultato per il semicerchio, ovvero esattamente per quanto raccontato nel problema di Didone.
Curve e angoli
La distanza temporale tra Zenodoro e Pappo e i loro rispettivi risultati è all'incirca di 6 secoli. E ce ne vorranno ancora di più per arrivare da Pappo a Jakob Steiner, matematico svizzero che nel 1838 riuscì finalmente a dimostrare quella che mi permetto di chiamare congettura di Zenodoro. O quasi.Steiner sviluppò un metodo oggi noto come simmetrizzazione di Steiner e che Richard Tapia racconta in tre passi (in questa presentazione in pdf).
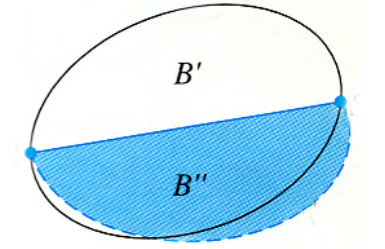
- Passo 1: si prende una curva convessa (se in una curva chiusa colleghiamo due punti qualsiasi del suo perimetro con un segmento e questo segmento non taglia la curva a parte i due estremi del segmento, allora questa curva è convessa, ma se esiste almeno un segmento per cui ciò non avviene, allora la curva è concava)
- Passo 2: la bisettrice del perimetro (il segmento che divide il perimetro a metà) divide la curva in due aree uguali e la si può simmetrizzare attraverso la bisettrice
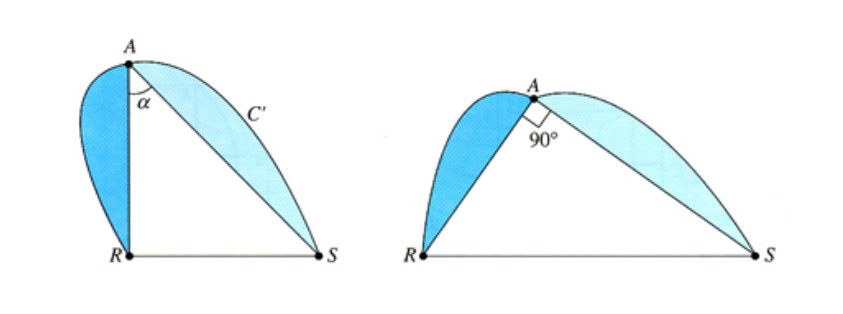
- Passo 3: tutti gli angoli inscritti determinati dalla bisettrice del perimetro devono essere angoli retti

E così alla fine ciò che Didone intuì nella sua ricerca del luogo perfetto dove fondare Cartagine venne finalmente dimostrato dalla curiosità di alcuni matematici attraverso i secoli.


Nessun commento:
Posta un commento