
(...) e questa volta svanì piuttosto lentamente, iniziando dalla punta della coda e finendo con il sogghigno, che rimase per un po' dopo che il resto era scomparso.L'immagine del sogghigno del gatto del Cheshire non è, però, un'idea completamente originale di Lewis Carroll. C'è, infatti, un riferimento nell'edizione del 1788 di A Classical Dictionary of the Vulgar Tongue di Francis Grose:
"Be'! Ho visto spesso un gatto senza un sogghigno" pensò Alice, "ma un sogghigno senza un gatto! E' la cosa più curiosa che abbia mai visto in tutta la mia vita!"
Cheshire cat. He grins like a Cheshire cat; said of any one who shows his teeth and gums in laughing.Ancora nel 1792 John Wolcot in Pair of Lyric Epistles scrive:
Lo, like a Cheshire cat our court will grin.E infine, nel 1855, dieci anni prima della pubblicazione dell'edizione completa di Alice nel Paese delle Meraviglie nel romanzo The Newcomes di William Makepeace Thackeray troviamo la abbastanza sarcastica frase:
That woman grins like a Cheshire cat.L'origine del detto è abbastanza ignota, e c'è una supposizione legata al fatto che nel Cheshire c'è così tanta abbondanza di latte e crema che i gatti lì sghignazzano. Nel caso del Gatto del Cheschire per eccellenza, però, è probabilmente un misto tra follia e puro e semplice divertimento. Sta di fatto, però, che l'idea del gatto che scompare e più in generale di una immagine che si strasforma era particolarmente gradita a Carroll, che ideò un particolare porta francobolli. Sui due lati erano realizzate due scene tratte dal romanzo, una quella di Alice con in braccio il bambino della Duchessa, e l'altro proprio il Gatto. Quando l'astuccio con i francobolli veniva estratto dal porta francobolli, le due immagini si trasformavano, lasciando Alice con in braccio un maialino da un lato e il solo sogghigno del Gatto dall'altro!
Alice e il Gatto sono, però, protagonisti di un divertente rompicapo ideato da Sam Loyd che coinvolge la frase palindroma Was it a cat I saw?. Arrangiamo le 13 lettere come nella figura qui sotto, tratta ovviamente dal rompicapo originale:

Nella sua soluzione originale, Loyd affermò la risposta più ovvia, \(24^2\) era quella sbagliata. Il ragionamento è semplice: essendoci 24 lettere sul bordo esterno del quadrato, ci saranno 24 modi per raggiungere la C al centro e altri 24 modi differenti per raggiungere una qualsiasi W sul bordo, e quindi \(24 \times 24 = 576\) modi diversi. Questo ragionamento, però, è errato, o quanto meno parziale, perché conta un solo possibile percorso per ciascuna W, quando in realta ce ne sono molti di più, per la precisione \(252^2 = 63504\). Come si è arrivati a questo numero? E soprattutto, è possibile generalizzare il risultato?
Sulla prima questione la faccenda è contare i percorsi. Poiché all'inizio mi era sfuggito il fatto dell'esistenza delle mosse consentite (sono partito dal rompicao così come era scritto su Il libro dei rompicapi di Alice di John Fisher), mi stavo mettendo a contare anche i percorsi con le diagonali, per cui ero partito sin da subito con l'idea di generalizzare. Poi, però, quando mi sono messo alla ricerca del testo originale, ecco spuntare le mosse consentite, il che semplificava un po' la faccenda.
L'idea era partire da un grafico a puntini, eliminando così qualsiasi lettera distraente, e contare in quanti modi ciascun puntino sul bordo può raggiungere il puntino al centro utilizzando solo mosse tipo su, giù, destra, sinistra. Per semplicità di calcolo bastava ridursi a un quarto del quadrato, escludendo una delle due tra la riga orizzontale e quella verticale. Questo perché di linee che vanno direttamente dal bordo al centro ce ne sono già quattro. In questo modo il risultato ottenuto per un quarto del quadrato moltiplicato per 4 ci restituisce il numero cercato da elevare poi al quadrato. Concentriamoci, quindi sugli altri puntini.

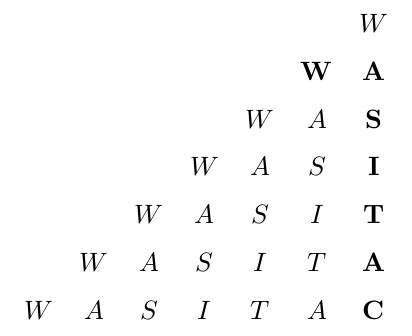
Il numero di passi che dovremo compiere per arrivare dal bordo al centro sarà pari a \(n\), per cui dovremo calcolare tutte le combinazioni che vanno da nC0 fino a nC(n-1), sommarle e moltiplicarle per 4 e, infine, elevare il risultato al quadrato, ottenendo così una procedura quanto più generale possibile.
Ultima curiosità per chiudere il tutto: nel gioco della vita di Conway (ne abbiamo parlato in una vecchia puntata dei Rompicapi), è stata scoperta una forma chiamata Gatto del Cheschire che partendo da una configurazione che ricorda il volto di un gatto evolve in una specie di sogghigno per poi ridursi a un quadrato costituito da quattro celle: anche tra gli automi cellulari il Gatto di Carroll ama combinare scherzi, in questo caso ai matematici!
P.S.: oltre alla soluzione di Chen, ho trovato altre due soluzioni, ma trovo che quella di Chen sia la più semplice da generalizzare.

Nessun commento:
Posta un commento