I rompicapi di Alice: Il fantastico mondo dei politopi

La serie dei Rompicapi di Alice nasceva, ai tempi in cui Science Backstage era ospitato sull'ormai defunta Blogosfere, per proporre articoli più o meno brevi intorno al mondo di Alice nel paese delle meraviglie e del suo autore, Lewis Carroll. La guida che utilizzavo all'inizio, e che alcune volte utilizzo ancora adesso, era Il libro dei rompicapi di Alice di John Fisher, un'utile e interessante raccolta di molti dei rompicapi carrolliani usciti sia sui suoi volumi, sia sulle riviste con le quali collaborava. Oltre, ovviamente, ad altre curiosità.
A questi spunti iniziali, si aggiungevano anche ricerche personali su "cose carrolliane" non prese in considerazione da Fisher, o, in puro spirito carrolliano, diventavano punti di partenza per andare in direzioni leggermente differenti. La serie, però, non si è limitata solo ai rompicapi di Carroll, ma l'ho utilizzata per raccontare anche altre questioni presenti nella matematica, in particolare ricreativa, utilizzando altri punti di riferimento del campo, su tutti Martin Gardner.
L'articolo di oggi ricadrebbe in questa seconda categoria, ma molto più di altri merita di avere l'Alice nel titolo, come scoprirete se avrete la pazienza di leggerlo tutto (anche se chi legge il blog da un po', potrebbe intuirlo!).

Poligoni, poliedri e oltre

Siamo tutti abituati a pensare a poligoni e poliedri utilizzando la visione tridimensionale che ci è stata donata dalla natura. Eppure queste figure geometriche possono essere viste anche in dimensioni superiori. Il primo (o quanto meno uno dei primi) a fare qualcosa del genere fu August Ferdinand Möbius che nel 1827 scoprì che due solidi speculri possono essere sovrapposti ruotando uno di essi attraverso una opportuna quarta dimensione.
Qualche anno più tardi, nel 1850, furono Arthur Cayley e Hermann Grassmann a prendere in considerazione le dimensioni superiori.
Il primo che, però, immaginò l'esistenza degli analoghi di poligoni e poliedri in dimensioni superiori fu Ludwig Schläfli nel 1852: il suo articolo, in cui descriveva i sei quadri-politopi convessi regolari non venne, però, pubbliato fino al 1901, sei anni dopo la sua morte. Il lavoro di Schläfli, tra l'altro, anticipava di un paio di anni quello di Bernhard Riemann che di fatto dava inizio alla ricerca matematica nelle geometrie a dimensioni superiori a 3.
I politopi regolari di Schläfli, comunque, vennero più volte ri-scoperti da altri matematici nel corso degli anni successivi. Il primo in questa lista fu Washington Irving Stringham nel 1880. Il suo articolo forniva una dimostrazione intuitiva dei sei politopi regolari, fornendo delle istruzioni esplicite per la loro costruzione. All'interno dello stesso era presente una delle prime (se non la prima) illustrazioni di figure quadridimensionali:

Dall'articolo di Stringham - via Alicia Boole Stott, a geometer in higher dimension di Irene Polo-Blanco

Ovviamente esse sono rappresentazioni bidimensionali di proiezioni tridimensionali di altrettante figure quadridimensionali. Per capire tutto ciò basti pensare in termini flatlandesi (ogni riferimento al romanzo matematico Flatland di Edwin Abbott non è per nulla casuale!). Se un qualsiasi abitante del mondo bidimensionale di Flatland, superata la propria chiusura mentale sull'esistenza di oggetti tridimensionali, volesse indagare le proprietà di un qualsiasi solido platonico, dovrebbe esaminare le sue sezioni trasversali. A seconda di come il solido platonico taglia il piano di Flatlandia, la sua sezione potrebbe risultare una figura geometrica leggermente differente: per esempio se prendiamo un ottaedro, alcune sue sezioni potrebbero risultare esagonali, altre quadrate, altre ancora rettangolari.
Allo stesso modo se prendiamo una figura geometrica quadridimensionale, questa taglierà il nostro mondo tridimensionale generando delle sezioni differenti a seconda di come attraversa il nostro spazio. Ovviamente ciascuna di queste sezioni risulterebbe un solido differente.
I solidi rappresentati da Stringham sono proprio queste sezioni, o, appunto, proiezioni tridimensionali.
E una delle matematiche che diede maggiore impulso alla scoperta di tali proiezioni, realizzando anche dei modellini veri e propri, fu Alicia Boole, sia da sola sia in collaborazione con Pieter Hendrik Schoute.

Una teca con i modeli di Alicia Boole conservati presso l'università di Groningen

Particolarmente interessante è la visualizzazione dell'iperoctaedro (hyperoctahedron) presentata in un suo articolo del 1900, On certain series of sections of the regular four-dimensional hypersolids. La proiezione tridimensionale di questo particolare solido quadridimensionale è costituita da 16 tetraedri, di cui nel disegno qui sotto ne vediamo cinque:

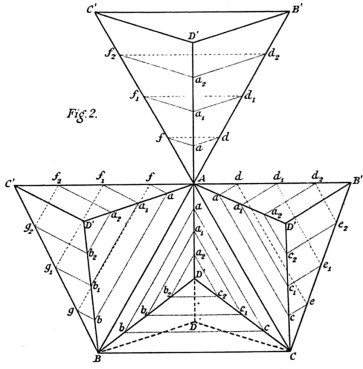
Un disegno di Alicia Boole - via Alicia Boole Stott, a geometer in higher dimension di Irene Polo-Blanco

Sempre nello stesso articolo troviamo lo sviluppo degli ipersolidi 120-celle e del suo duale 600-celle. E' dunque interessante confrontare il diagramma di uno di questi due ipersolidi, nel dettaglio il 600-celle, realizzato da Schoute nel 1894 su Regelmässige Schnitte und Projektionen des Hundertzwanzigzelles und Sechshundertzelles im vierdimensionalen Räume, con il modello di Alicia Boole conservato presso il museo dell'Università di Groningen:

via Alicia Boole Stott, a geometer in higher dimension di Irene Polo-Blanco

Mi metterei qui a mostrarvi altri politopi di Alicia Boole (che tra l'altro inglesizzò il termine tedesco polytop con cui, nel 1882, Reinhold Hoppe iniziò a identificare questi particolari oggetti geometrici), ma penso di chiudere con quella che la stessa matematica chiama una "esansione" di un ottaedro, ovvero un ottaedro troncato:

via Alicia Boole Stott, a geometer in higher dimension di Irene Polo-Blanco

Un'espansione è realizzata considerando un poliedro regolare e l'insieme dei suoi vertici, spostando ogni elemento dell'insieme di una certa distanza dal centro del poliedro. Tutte queste distanze sono uguali e questo nuovo insieme esteso di vertici definisce un poliedro semiregolare. Boole presen in considerazione il caso particolare dell'espansione applicata ai solidi platonici rispetto ai suoi lati, scoprendo che il risultato era il medesimo solido, ma troncato, ovvero con tutti gli angoli tagliati.
Ultima curiosità prima di chiudere: nel 2013 è stato scoperto che l'amplituhedron (amplituedro) permetterebbe di semplificare alcuni calcoli in fisica teorica.

Approfondisci

• The Princess of Polytopia: Alicia Boole Stott and the 120-cell di Tony Phillips
• Alicia Boole Stott, a geometer in higher dimension di Irene Polo-Blanco
• The Classification of Archimedean 4-Polytopes (pdf) di Robin Whitty