Ritratti: Martin David Kruskal

A parte gli argomenti su cui ho lavorato direttamente (alcuni con pochi frutti, purtroppo) una delle "curiosità" fisiche a cui mi sono avvicinato durante gli anni di dottorato è stata il concetto del solitone, ovvero un'onda solitaria ad esempio in grado di risalire la corrente dell'Union Canal in Scozia. E' stato proprio su quel canale che il solitone venne osservato per la prima volta nel 1834 dall'ingegnere John Scott Russell:

Stavo osservando il moto di una barca che veniva rapidamente trascinata da una coppia di cavalli lungo uno stretto canale, quando la barca si fermò improvvisamente, ma non così la massa d'acqua nel canale che aveva messo in moto; si accumulò intorno alla prua del vascello in uno stato di violenta agitazione, quindi allontanandosi immediatamente, rotolò in avanti con grande velocità, assumendo la forma di una larga vetta solitaria, un mucchio d'acqua arrotondato, liscio e ben definito, che continuò la sua corsa lungo il canale apparentemente senga cambiare forma o diminuire velocità. La seguii a cavallo, e la raggiunsi mentre stava ancora rotolando a circa 8 o 9 miglia all'ora, conservando la sua forma originale lunga all'incirca 30 piedi e alta tra un piede e un piede e mezzo. La sua altezza diminuì gradualmente, e dopo un inseguimento di una o due miglia la persi tra le curve del canale. Tale, nel mese di agosto del 1834, fu il mio primo casuale incontro con quel singolare e bellissimo fenomeno che ho chiamato onda di traslazione⁽¹⁾.

Per fornire una comprensione teorica del fenomeno osservato da Russell (e a cui molti guardavano con scetticismo, visto che non era previsto dai modelli all'epoca in voga) bisogna attendere gli anni Sessanta del XX secolo e il contributo del matematico e fisico Martin David Kruskal.

Origami e grandi domande

Martin Kruskal

Nato il 28 settembre del 1925 a New York da una famiglia ebrea, era uno dei cinque figli di Joseph Kruskal, uomo d'affari di successo, e Lillian Vorhaus, diventata famosa come esperta di origami, fondando l'Origami Center of America, oggi OrigamiUSA. Aveva due sorelle e due fratelli, William Kruskal e Joseph Kruskal Jr, diventati entrambi matematici: evidentemente la passione dei numeri era forte tra i figli maschi dei Kruskal!
Tra l'altro Martin nel 1950 sposò una (passatemi il termine) origamista, Laura Kruskal, ricordata come una delle più prolifiche ideatrici di questa artistica forma di piegatura della carta. D'altra parte anche Martin era un appassionato di origami: la moglie Laura, infatti, ricordava che si erano conosciuti proprio nella sede dell'associazione fondata dalla madre di Martin⁽²⁾.
Dei loro tre figli, Karen, Kerry, and Clyde, solo quest'ultimo intraprese la carriera scientifica, nel campo dell'informatica precisamente. Le due figlie, invece, sono rispettivamente avvocatessa e scrittrice di libri per bambini.
Kruskal, da appassionato di giochi e rompicapi (ne ha anche ideato uno, ma ne discuteremo in separata sede), si ingegnava nel realizzare ma anche nell'ideare diversi origami, come ad esempio quello che regalò a Sheila Gibbon durante una conferenza in Europa. L'occasione era dovuta a uno strano aneddoto: a un certo punto Kruskal, nel corso della colazione, inizia a interrogare un barattolo di marmellata chiedendosi cose come Perché è rotondo e non quadrato?, Perché non è esagonale o addirittura ottagonale?, Perché il coperchio non è più spesso?, Perché l'etichetta è rosa e non verde?. A rispondere a questo attacco di percheitudine (scusatemi ancora una volta!) ci pensò proprio Sheila con il classico Oh, non lo so, Martin⁽²⁾.
Era dunque una persona interessata a capire i perché delle cose e si interessò a argomenti dei più disparati, come testimonia la vignetta che gli ha dedicato Leo Cullum sul New Yorker⁽²⁾:

Di tutta questa prolifica attività, però, vi racconterò (nel più breve spazio possibile, o almeno ci proverò!) giusto un paio di risultati.

Una storia singolare

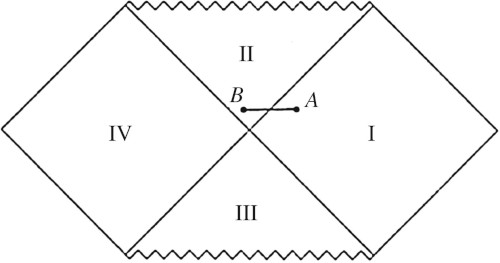
Forse più che una storia singolare è una storia intrecciata, che faccio iniziare nel 1960, quando Kruskal, indipendentemente da George Szekeres⁽³⁾, propose un'estensione della metrica di Schwarzschild⁽⁴⁾, che mostrava come, usando le oggi note coordinate di Kruskal, alcune soluzioni delle equazioni della relatività generale che sono singolari all'origine, non sono più singolari all'allontanarsi dall'origine⁽⁵⁾. L'articolo, quindi, si occupoa dei buchi neri, quelli introdotti da Karl Schwarzschild, e sfocia in un più ampio discorso che coinvolge i ponti di Einstein-Rosen (o wormhole).
Il fatto interessante è, in effetti, che questo wormhole, che dovrebbe mettere in collegamento due regioni dello spaziotempo (la I e la IV nel diagramma di Penrose qui sotto) confinanti con un buco nero (la II) può essere attraversato solo a velocità superiori a quella della luce⁽²⁾!

La storia, però, si fa curiosamente intrecciata, come anticipavo, quando andiamo a vedere con chi, tra gli altri, Kruskal si occupò di fisica del plasma: Martin Schwarzschild⁽⁶⁾, figlio proprio di quel Karl lì, quello dei buchi neri!
Il lavoro con Martin Schwarzschild rientrava all'interno del progetto noto come Matterhorn, all'epoca segreto. A reclutarlo fu l'astrofisico Lyman Spitzer e l'obiettivo del progetto era studiare la fattibilità di una fusione nucleare controllata, in particolare la possibilità di poter mantenere sotto controllo il plasma usando degli opportuni campi magnetici.
Il lavoro per il Matterhorn produsse una serie di risultati pubblicati in una decina di articoli. L'interesse di Kruskal nei confronti della fisica del plasma, però, iniziò a venire meno quando il matematico iniziò a interessarsi proprio del problema da cui siamo partiti: i solitoni.

Un'onda solitaria verso il tramonto

Il principale problema nell'osservazione del solitone da parte di Russell era che la natura del fenomeno restò sostanzialmente ignota per diverso tempo. I modelli fluidodinamici dell'epoca non erano abbastanza raffinati da descrivere in modo sufficientemente corretto un fluido e quindi da prevedere l'esistenza di queste particolari onde solitarie. Ovviamente Russell realizzò anche degli esperimenti in una situazione controllata (una vasca a casa) e i suoi risultati gli permisero di stabilire che:

• le onde sono stabili e possono viaggiare per grandi distanze;
• la velocità dipende dalle dimensioni dell'onda, mentre la sua larghezza dalla profondità dell'acqua;
• A differenza delle onde normali, non si uniscono mai, quindi quando un piccolo solitone ne incontra uno grande, i due non si fondono, ma, diciamo così, si attraversano;
• se un'onda è troppo grande rispetto alla profondità dell'acqua, si divide in due, una grande e l'altra piccola.

Un primo passo avanti venne fatto nel 1895 quando Diederik Korteweg e Gustav de Vries proposero la oggi nota equazione di Korteweg–de Vries⁽⁷⁾ che includeva come soluzioni anche le onde solitarie.
Il vero avanzamento ci fu, però, nel 1965 grazie proprio a Martin Kruskal, all'epoca presso l'università di Princeton, e Norman Zabusky dei Bell Labs. I due dimostrarono il comportamento dei solitoni in mezzi soggetti all'equazione di Korteweg–de Vries utilizzando il calcolo computazionale⁽⁸⁾. E furono anche loro a introdurre la parola soliton per indicare questo genere di onde.
La cosa interessante è che i due stavano in realtà cercando una soluzione a un apparente paradosso presente in uno dei primissimi sistemi simulati al computer, un reticolo non lineare progettato da Enrico Fermi, John Pasta e Stanislaw Ulam nei laboratori di Los Alamos nel 1955 (il problema è oggi noto come problema di Fermi-Pasta-Ulam-Tsingou). In particolare Kruskal aveva ottenuto l'equazione di Korteweg–de Vries come limite continuo di una catena unidirezionale di oscillatori armonici. Simulando tale equazione Zabusky e Kruskal ottennero proprio il comportamento solitonico, molto diverso dall'equlibrio termico che si aspettavano Fermi e compagni.

E' ironico che in un periodo in cui molte domande⁽⁹⁾ di finanziamento in tutto il mondo richiedono la presenza dell'interdisciplinarietà nelle proposte ricevute, un Martin senza finanziamenti sia stato uno dei primi fondatori di questo stile di scienza interdisciplinare. Ai suoi occhi, l'interdisciplinarietà non era né una posizione istituzionalizzata né un esercizio da spuntare, ma semplicemente il modo in cui lavorava.⁽²⁾

---

1. Scott Russell, J. (1845). Report on Waves: Made to the Meetings of the British Association in 1842–43. ↩︎
2. Gibbon, J. D., Cowley, S. C., Joshi, N., & MacCallum, M. A. H. (2018). Martin David Kruskal. 28 September 1925—26 December 2006. doi:10.1098/rsbm.2017.0022 ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
3. Szekeres G. (1960). On the singularities of a Riemannian manifold. Publ. Mat. Debrecen 7, 285–301; reprinted 2002 in Gen. Rel. Grav. 34, 2001. ↩︎
4. Kruskal, M. D. (1960). Maximal extension of Schwarzschild metric. Phys. Rev. 119, 1743–1745. doi:10.1103/PhysRev.119.1743 ↩︎
5. John O'Connor, Edmund Robertson, Martin David Kruskal, MacTutor History of Mathematics archive, University of St Andrews. ↩︎
6. Kruskal, M. D., Schwarzschild M. (1954). Some instabilities of a completely ionized plasma. Proc. R. Soc. Lond. A 223, 348–360. ↩︎
7. Korteweg D. J. & de Vries G. (1895). On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Phil. Mag. 39, 422–443. ↩︎
8. Zabusky N. J., Kruskal, M. D. (1965). Interaction of 'solitons' in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240–243. doi:10.1103/PhysRevLett.15.240 ↩︎
9. In realtà è funding agencies, agenzie di finanziamento, ma in italiano non abbiamo un concetto così esplicito e ampio, per cui ho optato per domande ↩︎