
canta, canta, canta, canta all'albaLa poesia gaussiana redatta con grande impegno da Marco Fulvio Barozzi in arte Popinga è una struttura poetico-matematica abbastanza semplice da comprendere. Una volta capito come si alternano i versi si può trasformare (quasi) qualisiasi numero in un verso partendo dalla sua fattorizzazione. E per il 176, numero d'ordine del Carnevale della Matematica che vi apprestate a leggere, la sua fattorizzazione è pari a \[2^4 \times 11\] per cui dall'unione dei versi corrispondenti ai "due" fattori, ecco il verso d'apertura della special edition odierna.
Perché, come spero ricorderete (e l'orario di uscita del Carnevale è in questo un indizio significativo) oggi è il pi day, che ormai dal lontano 2012 con l'edizione #47 viene festeggiato qui su DropSea. Come è ovvio, quindi, il tema portante di questa edizione è proprio il pi greco, che sarà protagonista non solo in alcuni dei contributi che mi appresso a presentare, ma anche grazie alle ormai usuali notizie pi greche, i piccoli box con i quali nel corso degli anni ho cercato di raccontare la storia e altre curiosità del numero più famoso del mondo. Per cui questa introduzione al Carnevale è dedicata al 176.
Questi è un numero pari i cui divisori sono: 1, 2, 4, 8, 11, 16, 22, 44, 88, 176. Se li sommiamo insieme, 176 escluso, otteniamo 196, maggiore di 176, il che fa di quest'ultimo un numero abbondante. Se però alla somma di prima togliamo il 4 e il 16 otteniamo proprio 176, il che lo rende un numero semiperfetto.
Fa poi parte delle seguenti terne pitagoriche:
(57, 176, 185), (132, 176, 220), (176, 210, 274), (176, 330, 374), (176, 468, 500), (176, 693, 715), (176, 960, 976), (176, 1932, 1940), (176, 3870, 3874), (176, 7743, 7745)
proprio come il 167, ovvero il protagonista dell'edizione 2023, è un numero felice. E visto che vi voglio bene, invece di rimandarvi a quell'edizione, vi (ri)definisco qui la felicità:Prendiamo un numero. Eleviamo al quadrato ciascuna delle sue cifre. Quindi sommiamole. Ripetiamo l'operazione con il risultato ottenuto. Proseguendo si può ricadere in due situazioni: il ciclo finisce con 1; il ciclo non finisce mai con 1 e, anzi, entra in un loop. Nel primo caso il numero si dice felice. E questa è la felicità del 176: \[1^2 + 7^2 + 6^2 = 86\] \[8^2 + 6^2 = 100\] \[1^2 = 1\] Come qualcuno avrà notato, la cosa non poteva che essere così, visto che le cifre del 176 sono una delle possibili permutazioni delle cifre del 167! Con le prossime due proprietà del 176 spero di non perdervi. Il 176, infatti, è un numero pratico. Il motivo è che tutti i numeri interi positivi precedenti al 176 possono essere scritti come somma di uno o più dei suoi divisori.
E' interessante osservare come due particolari congetture sui numeri primi, la congettura di Goldbach e la congettura dei numeri primi gemelli, che non sono ancora state dimostrate per i numeri primi, si sono rivelate vere per i numeri pratici. In pratica ogni numero pari può essere scritto come la somma di due numeri pratici, ed esistono ifniniti numeri pratici (m) tali che anche (m+2) è un numero pratico (in realtà i numeri pratici si spingono addirittura fino a terne di numeri pratici gemelli!).
Infine il 176 è un numero colombiano. Per spiegare cosa sono questi numeri faccio un esempio. Prendiamo il 43. Può essere scritto come 43 = 35 + 5 + 3. Notate che sia 5 sia 3 sono le cifre che compongono il 35. Ebbene il 43 non è un numero colombiano. Mentre, per esempio, il 42, o il nostro 176, è un numero colombiano poiché non esiste nessun intero positivo con il quale scrivere un'uguaglianza simile a quella scritta per il 43.
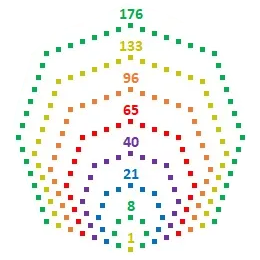
Lascio per ultima la proprietà che può essere rappresentata con una figura. Il 176, infatti, è un numero ottagonale poiché può essere rappresentato come un ottagono:
Pubblicato l'8 marzo, la Giornata internazionale della donna, il post parte da una riflessione su un tema di continua discussione sociale (purtroppo grazie anche alle parole di un certo generale), la "normalità", per ricordare la battaglia delle donne per conquistarsi un posto nelle discipline STEM, il ruolo della diversità nella scienza e nella società, il concetto di umanità (richiamando un bel film italiano recente).E passiamo a Maurizio Codogno, impegnato in questo periodo a curare la serie Matematica per Gazzetta dello Sport e Corriere della Sera. Questa la come sempre corposa lista dei suoi contributi:
Con questa premessa ci si spinge poi a parlare di normalità in un regno che non offende nessuno: quello della matematica. Ed ecco allora che avviene la presentazione dei cosiddetti numeri normali, tra cui si ipotizza (ma non è stato dimostrato) ci sia anche il sempre festeggiato pi greco.
Si inizia con i quizzini:
- Offerta speciale, che parla delle famose tavolette di cioccolato Tonka.
- Nove cifre, numerico e piuttosto semplice.
- Strada rossa e strada blu, che ci chiede se sia meglio lasciare la strada vecchia per la nuova. Nel caso, chiedere a Pitagora.
- Ballroom Dancing, sulle coppie danzanti a un ballo.
- The Mathematical Theory of Communication, di Claude Shannon e Warren Weaver. Il libro da cui è nata tutta la teoria dell’informazione.
- Le anime della matematica, di Vincenzo Vespri: una storia di come la matematica si è evoluta.
- La logica matematica di Paolo Caressa
- Funzioni ed equazioni di Roberto Zanasi
- Gli insiemi di Paolo Caressa
- Algebra lineare di Andrea Mercuri
- «54 milioni di italiani, sostanzialmente quasi tutti», sul contare le identificazioni essendo incapaci di capire che qualcuno può essere identificato più volte.
- Quando nacque il punto decimale?:il punto decimale è di un secolo e mezzo precedente rispetto a quanto si pensava.
- Le antiparallele, che ovviamente parallele non sono ma in un certo senso fanno finta.
- Come arrivare a pi greco, dove si mostra come una banale successione tende a pi greco; la spiegazione è qui.
Come da tradizione il Carnevale della Matematica di marzo è dedicato al Pi Day, ma dal 2020, il 14 marzo (3.14), si festeggia l’International Day of Mathematics curato dalla International Mathematics Union (IMU) proclamata dall’UNESCO.E questo mi sembra un buon punto per introdurre la prima delle notizie pi greche di questa 176.ma edizione:
Il tema di quest’anno è "Playing with Maths" (Giocare con la Matematica) che può significare anche ballare, danzare, suonare con la Matematica e quindi ripropongo un post che ricorda "giochi tangueri" proprio di quel pi day del 2020, anno in cui divenne appunto Giornata Internazionale della Matematica.
Notizie pi greche #33
L'era dei computer nel calcolo delle cifre decimali del \(\pi\) iniziò a metà del XX secolo. Nel 1949, infatti, utilizzando una semplice calcolatrice, John Wrench e Levi Smith calcolarono 1120 cifre decimali.
L'anno dopo George Reitwiesner e John von Neumann raggiunsero le 2037 cifre. Utilizzarono una serie infinita di arcotangenti sul computer ENIAC, che impiegò 70 ore per ottenere questo risultato. Proprio grazie alle serie delle arcotangenti il record venne battuto sempre più spesso negli anni successivi: 3089 cifre nel 1955, 5480 cifre nel 1957, 10000 cifre nel 1958, 100000 nel 1961, 1 milione di cifre nel 1973.
Negli anni Ottanta del XX secolo arrivò un nuovo strumento che permise di calcolare le cifre decimali del pi greco in maniera più veloce ed efficiente: gli algoritmi iterativi.
Questi algoritmi erano basati su metodi matematici che prevedevano la risuoluzione di un problema facendo uso di approssimazioni successive. Il metodo, in effetti, dovremmo averlo incontrato un po' tutti a scuola, visto che il così detto metodo di Newton per determinare gli zeri di una curva è esattamente un metodo o algoritmo iterativo, applicato in generale a una funzione in cui il metodo analitico risultava impossibile (o troppo lungo) da applicare.
Non è un caso, allora, che questo genere di algoritmi venne proposto tra il 1975 e il 1976, dal fisico Eugene Salamin e dal matematico Richard Brent. Nello specifico l'algoritmo di Brent e Salamin era una opportuna modifica all'algoritmo di Gauss o di Gauss-Legendre, sviluppato indipendentemente da Carl Friedrich Gauss e da Adrien-Marie Legendre proprio con lo scopo di calcolare il \(\pi\).
Il metodo è abbastanza semplice, in termini matematici. Si inizializzano le variabili: \[a_0 = 1, \qquad b_0 = \frac{1}{\sqrt{2}}, \qquad t_0 = \frac{1}{4, \qquad p_0 = 1}\] Si definiscono le seguenti iterazioni: \[a_{n+1} = \frac{a_n + b_n}{2}, \qquad b_{n+1} = \sqrt{a_n b_n},\] \[t_{n+1} = t_n - p_n (a_n - a_{n+1})^2, \qquad p_{n+1} = 2 p_n\] L'approssimazione di pi greco sarà quindi data da \[\pi \approx \frac{(a_{n+1}+b_{n+1})^2}{4t_{n+1}}\] In questo modo si riescono a ottenere 45 milioni di cifre corrette del pi dopo appena 25 iterazioni.
Dal quel momento in poi gli algoritmi iterativi vennero utilizzati sempre più spesso proprio in virtù della loro maggiore velocità rispetto alle serie infinite. Il motivo di tale velocità risiede nelle differenze tra i due metodi: le serie infinite procedono aggiungendo una cifra decimale a ogni passaggio, mentre gli algoritmi iterativi raddoppiano, triplicano, qadruplicano, ecc. (il tasso di avanzamento dipende dall'algoritmo) le cifre decimali a ogni passaggio. Per esempio nel 1984 i fratelli John e Peter Borwein realizzarono un algoritmo in grado di quadruplicare le cifre decimali dopo ogni iterazione. E fu proprio grazie agli algoritmi iterativi che Yasumasa Kanada stabilì diversi record nel calcolo di \(\pi\) tra il 1995 e il 2002.
Il problema è che questo genere di algoritmi richiedono una grande quantità di memoria, motivo per cui cedettero il passo alle serie rapidamente convergenti. Questa, però, è un'altra storia.
Dopo la pausa d'uopo eccoci nuovamente al regolare flusso di post insieme con i Rudi Mathematici:
L'era dei computer nel calcolo delle cifre decimali del \(\pi\) iniziò a metà del XX secolo. Nel 1949, infatti, utilizzando una semplice calcolatrice, John Wrench e Levi Smith calcolarono 1120 cifre decimali.
L'anno dopo George Reitwiesner e John von Neumann raggiunsero le 2037 cifre. Utilizzarono una serie infinita di arcotangenti sul computer ENIAC, che impiegò 70 ore per ottenere questo risultato. Proprio grazie alle serie delle arcotangenti il record venne battuto sempre più spesso negli anni successivi: 3089 cifre nel 1955, 5480 cifre nel 1957, 10000 cifre nel 1958, 100000 nel 1961, 1 milione di cifre nel 1973.
Negli anni Ottanta del XX secolo arrivò un nuovo strumento che permise di calcolare le cifre decimali del pi greco in maniera più veloce ed efficiente: gli algoritmi iterativi.
Questi algoritmi erano basati su metodi matematici che prevedevano la risuoluzione di un problema facendo uso di approssimazioni successive. Il metodo, in effetti, dovremmo averlo incontrato un po' tutti a scuola, visto che il così detto metodo di Newton per determinare gli zeri di una curva è esattamente un metodo o algoritmo iterativo, applicato in generale a una funzione in cui il metodo analitico risultava impossibile (o troppo lungo) da applicare.
Non è un caso, allora, che questo genere di algoritmi venne proposto tra il 1975 e il 1976, dal fisico Eugene Salamin e dal matematico Richard Brent. Nello specifico l'algoritmo di Brent e Salamin era una opportuna modifica all'algoritmo di Gauss o di Gauss-Legendre, sviluppato indipendentemente da Carl Friedrich Gauss e da Adrien-Marie Legendre proprio con lo scopo di calcolare il \(\pi\).
Il metodo è abbastanza semplice, in termini matematici. Si inizializzano le variabili: \[a_0 = 1, \qquad b_0 = \frac{1}{\sqrt{2}}, \qquad t_0 = \frac{1}{4, \qquad p_0 = 1}\] Si definiscono le seguenti iterazioni: \[a_{n+1} = \frac{a_n + b_n}{2}, \qquad b_{n+1} = \sqrt{a_n b_n},\] \[t_{n+1} = t_n - p_n (a_n - a_{n+1})^2, \qquad p_{n+1} = 2 p_n\] L'approssimazione di pi greco sarà quindi data da \[\pi \approx \frac{(a_{n+1}+b_{n+1})^2}{4t_{n+1}}\] In questo modo si riescono a ottenere 45 milioni di cifre corrette del pi dopo appena 25 iterazioni.
Dal quel momento in poi gli algoritmi iterativi vennero utilizzati sempre più spesso proprio in virtù della loro maggiore velocità rispetto alle serie infinite. Il motivo di tale velocità risiede nelle differenze tra i due metodi: le serie infinite procedono aggiungendo una cifra decimale a ogni passaggio, mentre gli algoritmi iterativi raddoppiano, triplicano, qadruplicano, ecc. (il tasso di avanzamento dipende dall'algoritmo) le cifre decimali a ogni passaggio. Per esempio nel 1984 i fratelli John e Peter Borwein realizzarono un algoritmo in grado di quadruplicare le cifre decimali dopo ogni iterazione. E fu proprio grazie agli algoritmi iterativi che Yasumasa Kanada stabilì diversi record nel calcolo di \(\pi\) tra il 1995 e il 2002.
Il problema è che questo genere di algoritmi richiedono una grande quantità di memoria, motivo per cui cedettero il passo alle serie rapidamente convergenti. Questa, però, è un'altra storia.
- Il primo post (dopo quello del Carnevale di Febbraio) è stato il cosiddetto "post istituzionale", la ragion d'essere del nostro blog: insomma, il post che raccoglie le soluzioni dei lettori di Le Scienze al problema che pubblichiamo ogni mese sull’augusta rivista. Il post si intitola L'ira funesta della Pelide Alice ed è facile intuire che, nel raccontino che riveste il quesito, la nostra Alice si sia arrabbiata molto.
- L'altro post è invece un compleanno: un compleanno che parte invero molto alla lontana, dalle origini della matematica occidentale addirittura, per poi finire col parlare di Angelo Genocchi. Il titolo è quello standard dei compleanni, formato da una data di nascita e un augurio: 5 Marzo 1817: Buon compleanno, Angelo!, ma il titolo originale con cui è uscito originariamente sul numero 230 della nostra e-zine era Breve storia del mondo (secondo Pitagora).
Mauro Merlotti, invece, con il suo Zibaldone scientifico ci propone un post dal titolo già di per se abbastanza esplicito: 4D
Come scritto nel post, ho cercato di raccontare come immaginarsi una realtà in 2D o 4D a noi che siamo confinati in 3D.Luigi Menna, invece, partendo da alcune riflessioni un po' di logica un po' personali sul suo Laboratorio matematico, ci conduce a un interessante articolo che ha scritto per la rivista Insegnare: Logicamente adulto.
Ovviamente esistono molti libri o articoli che parlano di questo a partire da Abbott con Flatlandia, ma qui mi sono limitato a dare qualche spunto di riflessione. Sono argomenti molto affascinanti per "matematici duri e puri" ma possono dare molte soddisfazioni.
E come già scritto nel precedente post 245, se si continua a forare il nostro cubo con una certa logica, si può costruire il setaccio di Wallis e qui si chiude il cerchio arrivando ancora a pi greco! Potenza della matematica.
Come avrete letto nell'elenco dei libricini della serie Matematica curata da .mau., tra gli autori c'è anche Roberto Zanasi con Funzioni ed equazioni, a proposito del quale Roberto c'ha scritto su un post pubblicitario. E come dargli torto?
A questo aggiunge anche un articolo dedicato a Isaac Newton che originariamente doveva far parte del libro stesso, ma che poi non è stato inserito per un cambio nel progetto.
E arriva il momento di un'altra colonna del Carnevale, Marco Fulvio Barozzi, che ci propone Beppo Levi, tra Torino, gli Appennini e le Ande:
Beppo Levi (1875-1961) è stato un matematico autore di articoli su logica, equazioni differenziali, variabili complesse, sul confine tra analisi e fisica. La sua carriera di matematico e divulgatore si sviluppò soprattutto tra Parma e l'Argentina, dove fu costretto a emigrare perché ebreo.Con Daniela Molinari torniamo in qualche modo proprio al tema dell'edizione, oltre a essere un articolo perfetto per introdurre la prossima notizia pi greca. Con Cerchi tra i banchi:
Ho proposto un po' di immagini e colori ritrovati tra le pieghe delle indicazioni ministeriali per la seconda liceo scientifico: ho raccolto un po' di file di Geogebra che propongo ai miei alunni, qualche suggerimento ritrovato tra le pagine del simpatico libretto Il Cerchio di Bruno Munari, fino ad arrivare ai quesiti proposti per la competizione Matematica senza Frontiere, visto che il tema della Giornata Internazionale della matematica è proprio il gioco.
Notizie pi greche #34

Un metodo moderno di calcolare le cifre del pi greco e alla portata di tutti è utilizzando l'app per smartphone e tablet phyphox. E' un'applicazione che permette di compiere diversi esperimenti grazie ai sensori presenti nei moderni cellulari. Oltre agli esperimenti presenti nell'installazione di default, nel sito ufficiale se ne trovano molti altri, incluso quello relativo al calcolo del \(\pi\): ovviamente l'ho provato per voi.
Il metodo arriva abbastanza in fretta a 3.14, dopo qualcosa come una quarantina di secondi, ma se ne allontana subito dopo. Inizia a restare un po' più stabilmente intorno al 3.14 dopo un paio di minuti. Quindi riprende a crescere, poi diminuisce e intorno al quarto minuto ritorna più o meno stabile oscillando intorno a 3.144 con un errore di all'incirca 0.005 (valutando i punti massimi e minimi raggiunti) fino a che intorno al 4.o minuto e 50 secondi finalmente riesce a restare intorno al 3.141 per due o tre secondi. Quindi aumentano le oscillazioni e perde anche la seconda cifra decimale intorno al quinto minuto. Di fatto questo andamento oscillante lo prosegue per un po' tutte le due ore che ho catturato e riproduce l'andamento oscillante della funzione \(N(r)/r^2\) dove \(N(r)\) è il numero di punti all'interno della circonferenza di raggio \(r\) legata a un problema connesso con l'esperimento proposto da phyphox: il problema del cerchio di Gauss.
In pratica ci si chiede quanti punti di un reticolo discreto si trovano all'interno di una circonferenza. Ovviamente, visto il legame della circonferenza con il pi greco, il passo per l'uso di questo approccio al calcolo delle cifre del \(\pi\) è breve!
E' interessante, comunque, notare come, con pochi calcoli (basta prendere una circonferenza di raggio unitario per rendersene conto) con un'estrazione casuale dei punti del reticolo quadrato, la probabilità che un punto ricada all'interno della circonferenza (bordo incluso) è di \(\pi / 4\).
Dopo la pausa della seconda notizia pi greca torniamo ai post carnevaleschi con MaddMaths!, la rivista di divulgazione matematica diretta da Roberto Natalini. E si parte proprio con una serie di articoli a tema, dedicati cioé alla Giornata Internazionale della Matematica:

Un metodo moderno di calcolare le cifre del pi greco e alla portata di tutti è utilizzando l'app per smartphone e tablet phyphox. E' un'applicazione che permette di compiere diversi esperimenti grazie ai sensori presenti nei moderni cellulari. Oltre agli esperimenti presenti nell'installazione di default, nel sito ufficiale se ne trovano molti altri, incluso quello relativo al calcolo del \(\pi\): ovviamente l'ho provato per voi.
Il metodo arriva abbastanza in fretta a 3.14, dopo qualcosa come una quarantina di secondi, ma se ne allontana subito dopo. Inizia a restare un po' più stabilmente intorno al 3.14 dopo un paio di minuti. Quindi riprende a crescere, poi diminuisce e intorno al quarto minuto ritorna più o meno stabile oscillando intorno a 3.144 con un errore di all'incirca 0.005 (valutando i punti massimi e minimi raggiunti) fino a che intorno al 4.o minuto e 50 secondi finalmente riesce a restare intorno al 3.141 per due o tre secondi. Quindi aumentano le oscillazioni e perde anche la seconda cifra decimale intorno al quinto minuto. Di fatto questo andamento oscillante lo prosegue per un po' tutte le due ore che ho catturato e riproduce l'andamento oscillante della funzione \(N(r)/r^2\) dove \(N(r)\) è il numero di punti all'interno della circonferenza di raggio \(r\) legata a un problema connesso con l'esperimento proposto da phyphox: il problema del cerchio di Gauss.
In pratica ci si chiede quanti punti di un reticolo discreto si trovano all'interno di una circonferenza. Ovviamente, visto il legame della circonferenza con il pi greco, il passo per l'uso di questo approccio al calcolo delle cifre del \(\pi\) è breve!
E' interessante, comunque, notare come, con pochi calcoli (basta prendere una circonferenza di raggio unitario per rendersene conto) con un'estrazione casuale dei punti del reticolo quadrato, la probabilità che un punto ricada all'interno della circonferenza (bordo incluso) è di \(\pi / 4\).
- Giocare con la matematica – Giornata Internazionale della matematica 2024: Dal 2019 in poi, il 14 marzo si festeggia la Giornata internazionale della Matematica. L'International Day of Mathematics è un progetto curato dalla International Mathematics Union (IMU) ed è stata proclamata dall’UNESCO. Maddmaths! celebra la giornata internazionale della matematica, e il tema di quest'anno è Playing with Maths – Giocare con la Matematica. In tutti i vari paesi si celebra la giornata nelle scuole e nelle piazze tramite svariati eventi, tra cui anche l'Italia: consulta, quindi, gli eventi italiani
- Giocando con la Matematica: Il 14 Marzo si celebra la Giornata Internazionale della Matematica. Quest'anno il tema è: Giocando con la Matematica. Il verbo giocare, dall'inglese to play, può riferirsi anche allo sport. E il binomio Matematica e Sport sta crescendo negli ultimi anni tra dati, modelli matematici e sviluppo tecnologico. Marco Menale propone una riflessione per La Lente Matematica.
- Concorso di fotografia per la Giornata Internazionale della Matematica 2024: La sfida creativa di quest'anno è un concorso fotografico: con la Math Remix – 2024 Creative Challenge siete invitati ad aggiungere la matematica a un oggetto o un luogo qualunque, condividendo una foto della vostra creazione. Il concorso è aperto a tutti, condividete la sfida con la vostra scuola o la vostra università! La scadenza di invio delle immagini fissata per l'11 marzo 2024.
Ogni tre giorni (il martedì, il giovedì e il sabato), alle 3:14, dal 14 marzo al 28 giugno, verrà pubblicato un problema matematico. Ci si può iscrivere su CALENΠARIO e, magari assieme ad altre persone, portare avanti una piccola sfida per chi darà le risposte più velocemente.Eccovi, ora, una serie di articoli a tema libero e fuori da qualsiasi rubrica:
Il progetto è stato realizzato grazie a MaddMaths!, Riccardo Moschetti, Roberto Zanasi. Si ringraziano Maria Angela Chimetto e Sergio Zoccante per il prezioso controllo dei quesiti.
- I colori che non ti aspetti... in una tesi di laurea in matematica: Storia di come, grazie a MaddMaths!, la vita di una studentessa di matematica ha preso una direzione inaspettata. Ce ne parla la protagonista, Chiara Biguzzi, neo-laureata in matematica presso l'Università di Bologna.
- Questa storia dell'origine della notazione per i numeri decimali: La prima apparizione del punto all’interno di un numero per separare la cifra delle unità dai suoi valori decimali è comunemente attribuita Christopher Clavius in un'opera del 1593. Ora però, in un recente articolo nella rivista Historia Mathematica, lo storico canadese Glen Van Brummelen ha rintracciato le origini di questa notazione in uno scritto del 1440 dell'astronomo ferrarese Giovanni Bianchini. Ce ne parla Riccardo Bellè.
- Il linguaggio del corpo potrebbe essere utile nell'insegnamento dei concetti matematici astratti: La comunicazione non verbale potrebbe potrebbe essere l’arma segreta dei docenti per migliorare l’apprendimento di concetti matematici astratti. I ricercatori della Colorado State University, come si legge sulla rivista Problems, Resources, and Issues in Mathematics Undergraduate Studies (PRIMUS), hanno mostrato come i gesti e il linguaggio del corpo possono essere utilizzati per spiegare idee algebriche astratte con cui gli studenti interagiscono difficilmente, quando sono presentate con metodi di insegnamento formali.
- Rivoluzioni matematiche: il Teorema di Abel-Ruffini: Con il numero di Marzo de Le Scienze troverete in allegato il diciottesimo dei venticinque volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al teorema di Abel-Ruffini ed è a cura di Chiara de Fabritiis.
- L’inclusione universitaria alla luce della diversità: In un mondo in cui l'accesso all'istruzione è un diritto fondamentale, l'inclusione universitaria diventa una priorità imprescindibile. Per questo è nata l'associazione Università Inclusiva che ha lo scopo di migliorare il percorso educativo di tutti gli studenti non vedenti e con disabilità visiva. In questa intervista con Emilia Fares, fondatrice dell'associazione, parliamo del lavoro svolto da Università Inclusiva per creare un mondo in cui l'uguaglianza di accesso all'istruzione diventi una realtà per tutti.
- Angolo di tiro ed expected goals: Vediamo e commentiamo le partite di calcio con sempre più dati a disposizione. È il caso degli expected goal, xG. Ma come si misura questo valore? Tra gli altri, con l'angolo di tiro. L'angolo di tiro fornisce "lo specchio di porta a disposizione" di chi tira. Maggiore è questo angolo, maggiore è la probabilità, e quindi l'xG, che l'azione si trasformi in un goal.
- Raffreddare il caffè con la matematica: Pausa caffè in compagnia. Arriva la tazzina fumante e tu continui a parlare. Ma il caffè va bevuto caldo e, quindi, ti chiedi "quanto tempo resta prima che si raffreddi?" Possiamo rispondere a questa domanda con l'equazione di raffreddamento di Newton.
Chi sono i tre giganti della fisica che hanno cambiato il mondo con le loro scoperte? Newton ed Einstein sono nomi familiari, ma c’è un terzo genio che merita lo stesso riconoscimento: James Clerk Maxwell, lo scozzese che ha svelato i segreti dell’elettromagnetismo. Maxwell era un matematico geniale, capace di anticipare di decenni le idee dei suoi colleghi. Ha usato la matematica come una lente per esplorare la natura, formulando la teoria che unifica luce, elettricità e magnetismo. Sulle tracce del Detective Maxwell è una serie podcast di Edoardo Provenzi, pubblicata nel corso del mese di Febbraio, che racconta le avventure di Maxwell, la bellezza dei fenomeni che ha spiegato e il suo modo unico di guardare al mondo. I sei episodi di questo podcast sono ora tutti disponibili sul nostro sito, su Spotify, Apple podcast e sulle principali piattaforme di streaming.Finalmente arriviamo alla parte conclusiva del Carnevale, quella con i contributi di chi lo ospita. Iniziamo con le recensioni. Come già sapete è iniziata da ormai un mesetto la serie Matematica di librini in formato tascabile abbinata con Gazzetta dello Sport. Ovviamente ho iniziato a seguire anche io l'inziativa, tanto da modificare al giovedì il mio giorno di passaggio dall'edicola e queste sono le recesioni dei primi 4 volumi:
- I numeri di Maurizio Codogno
- La logica di Paolo Caressa
- Funzioni ed equazioni di Roberto Zanasi
- Gli insiemi di Paolo Caressa
Nella sezione delle biografie, invece, ecco Margaret Bryan insegnante di fisica e astronomia, una delle prime a realizzare dei veri e propri libri scolastici con tanto di esercizi per gli studenti.
Per i Rompicapi di Alice ecco Il problema di Didone, raccontando così il legame tra la fondazione di Cartagine e la matematica, in particolare con un problema isoperimetrico che è stato dimostrato solo diversi secoli dopo.
Questo mi permette di passare al Cappellaio Matto dove ecco il post di appoggio al video dedicato proprio a questo problema isoperimetrico Topolino #3560: Il problema di Didone. Oltre a questo, però, ci sono anche altri due post di appoggio ai video di Disney Comics&Science: Topolino #3559: Lo sciame robotico, che oscilla tra matematica ed ecologia, e Topolino #3562: L'effetto fisarmonica, ad alto tasso cosmologico.
L'ultimissimo contributo è l'articolo, con video, Universo Pi Greco realizzato per POE Factory dell'Osservatorio Astronomico di Brera come Astrocuriosità del mese di marzo. Che mi sembra il modo migliore per chiudere questa lunga carrellata. Sperando, quindi, di avervi tenuto compagnia, non mi resta che chiudere, come ormai da consolidata tradizione, con la cellula melodica di Flavio Ubaldini all’insegna di un luminoso intervallo di quinta:


Nessun commento:
Posta un commento