Come scritto nell'ultima edizione di Matematica in vacanza, invece di mettere in pausa Scienza take away accorpandola in MIV, come accaduto nel corso dell'anno precedente, ho deciso di pubblicare una nuova puntata di questa rubrichetta in virtù del gran numero di post extra-matematici usciti nel corso delle ultime 4 settimane (o giù di lì).
A differenza di altre occasioni, ho deciso di fare una suddivisione non già in blog, ma per argomenti, anche perché uno degli argomenti ha contribuito in maniera particolarmente corposa.
Stomachion
martedì 15 luglio 2025
lunedì 14 luglio 2025
Matematica in vacanza #4: giugno-luglio 2025
Ed è venuto quel momento dell'anno in cui il Carnevale della Matematica si prende una vacanza. Così, un anno dopo aver iniziato questa serie, rieccoci qui con Matematica in vacanza per raccogliere i post matematici che ho scritto nel corso del mese precedente.
Dopo aver dato un'occhiata al terzo numero, a differenza delle edizioni precedenti, poiché la sezione non-matematica sarebbe esageratamenteo più vasta rispetto a quella matematica, ho deciso di inserire in questo link post solo quelli matematici, per quanto pochi, dandovi appuntamento a Scienza take away, che uscirà domani.
Dopo aver dato un'occhiata al terzo numero, a differenza delle edizioni precedenti, poiché la sezione non-matematica sarebbe esageratamenteo più vasta rispetto a quella matematica, ho deciso di inserire in questo link post solo quelli matematici, per quanto pochi, dandovi appuntamento a Scienza take away, che uscirà domani.
domenica 13 luglio 2025
Topolino #3633: Fidarsi, ma di chi?

Testi mette Topolino di fronte a un dilemma: fidarsi, appunto, di Baskerville, che sta collaborando con Basettoni in modo particolarmente proficuo, o di Gambadilegno, che vuole convincerlo che i metodi di Baskerville non sono proprio "puliti". E c'è un momento chiave, esattamente dopo 2/3 della storia, in cui lo sceneggiatore crea le condizioni per dare una svolta a quei dubbi, in una scena molto ben rappresentata da Mazzarello, abile ormai nel gestire le atmosfere di genere.
sabato 12 luglio 2025
Zio Paperone #84: Il segreto di Molly Mallard

Secondo l'albero genealogico di Don Rosa, Molly era sposata con Dingus De' Paperoni, detto il sozzo, e i ritratti che ne fece il fumettista del Kentucky non erano esattamente felici: mostravano, infatti, una Molly depressa e un Dingus dal piglio arcigno (come il tipico esponente del clan De' Paperoni) e vestito nella foggia dei minatori.
Lo stesso Rosa, che ne aveva realizzato la foggia a partire sia dalle informazioni presenti nell'albero genealogico privato di Carl Barks, sia a partire dalle informazioni contenute in particolare ne Il clan di Zio Paperone, immaginava la storia di Molly e Dingus molto poco adatta al mondo disneyano. E dunque, con queste premesse, il compito delle autrici de La doppia vita di Molly Mallard lo si può immaginare particolarmente complicato.
venerdì 11 luglio 2025
Una lega spaziale

In sintesi questo nuovo materiale ha un comportamento termodinamico contro-intuitivo, poiché si restringe quando viene riscaldato e si espande quando si raffredda.
giovedì 10 luglio 2025
I paralipomeni di Alice: Ritorno alla locanda

Date le velocità di percorrenza ricavabili dal testo di Carroll relative ai tratti in pianura, \(s_p\), salita, \(s_s\), e discesa, \(s_d\), possiamo scrivere le equazioni che ci permettono di ricavare i tempi di percorrenza: \[t_p = \frac{s_p}{4}, \; t_s = \frac{s_s}{3}, \; t_d = \frac{s_d}{6}\] Il tempo totale, che sappiamo essere di 6 ore, è quindi dato dalla somma dei tre tempi di cui sopra: \[\frac{3 s_p + 4 s_s + 2 s_d}{12}\] Facciamo una prima semplificazione, ricordando che il tempo totale percorso dai due ospiti della locanda è \(s = s_p + s_s + s_d\), e quindi: \[\frac{3s + s_s - s_d}{12} = \frac{3s}{12} = \frac{s}{4}\] dove si ricorda che lo spazio in salita e quello in discesa sono identici e quindi si annullano.
E come detto il tempo di percorrenza è pari a 6 ore, e quindi siamo in grado di calcolare quanto i due turisti hanno percorso: 24 miglia. Che poi è proprio la soluzione indicata da Carroll nella sua rubrica.
mercoledì 9 luglio 2025
La potenza della Terra
In questi giorni le persone sui social, a seconda del loro credo, hanno condiviso "cose" per dimostrare che il singolo evento meteorologico era una conferma dei cambiamenti climatici, in particolare del riscaldamento globale, oppure uno dei tanti eventi estremi che ci sono stati anche in passato e concludere, quindi, "niente cambiamenti o riscaldamenti".
Il problema di fondo di queste condivisioni è che giocano soprattutto a favore di questi ultimi, e questo perché il singolo evento meteorologico non ci dice nulla sul clima.
Il clima, infatti, viene generalmente descritto da una serie di parametri termodinamici, come pressione, temperatura, ecc., raccolti in un arco di tempo lungo, tipicamente anni. E dunque si può parlare di cambiamenti climatici proprio perché, tra dati diretti, raccolti da stazioni meteorologiche e satelliti in orbita, e dati indiretti, raccolti grazie a prove geologiche (ma non solo), siamo in grado di ricostruire come il clima è cambiato sul nostro pianeta nel corso delle varie ere.
I fattori che influenzano il clima sono diversi: innanzitutto l'attività solare, quindi la concentrazione dei gas presenti nell'atmosfera (e d'altra parte il rapporto tra gli isotopi di particolari gas diventa anche un indicatore dei cambiamenti climatici), in particolare i famosi gas serra, e altri elementi tra cui la potenza termica irraggiata dalla Terra.
L'importanza della potenza termica irraggiata dalla superficie terrestre è strettamente connessa con la capacità dell'atmosfera di trattenere e rimandare verso la superficie tale radiazione, cosa che è regolata dalla concentrazione dei gas serra: in parole povere, per riprendere quelle scritte da Lawrence Krauss su La fisica del cambiamento climatico, l'atmosfera è responsabile di una specie di "effetto coperta". Poiché sulla questione dell'origine dei gas serra, per ora, non voglio dilungarmi, mi è sembrato interessante proporvi il grafico della potenza termica irraggiata dalla superficie del nostro pianeta così come è stata misurata dal Clouds and the Earth's Radiant Energy System della NASA. Ovviamente, maggiore è la radiazione che viene riflessa verso il basso dall'atmosfera, e più aumenterà quella che la Terra rimanderà verso l'alto.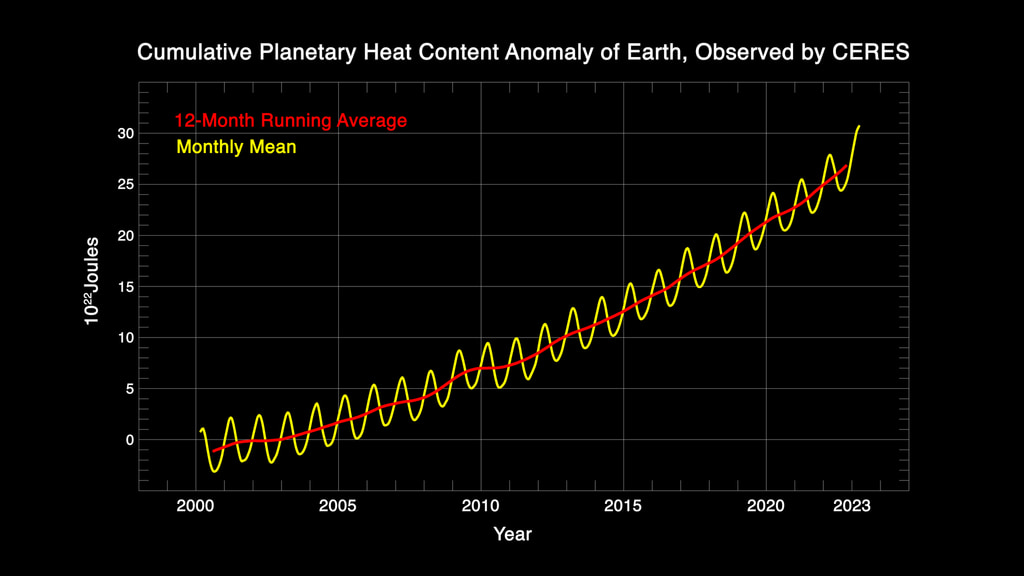
Il problema di fondo di queste condivisioni è che giocano soprattutto a favore di questi ultimi, e questo perché il singolo evento meteorologico non ci dice nulla sul clima.
Il clima, infatti, viene generalmente descritto da una serie di parametri termodinamici, come pressione, temperatura, ecc., raccolti in un arco di tempo lungo, tipicamente anni. E dunque si può parlare di cambiamenti climatici proprio perché, tra dati diretti, raccolti da stazioni meteorologiche e satelliti in orbita, e dati indiretti, raccolti grazie a prove geologiche (ma non solo), siamo in grado di ricostruire come il clima è cambiato sul nostro pianeta nel corso delle varie ere.
I fattori che influenzano il clima sono diversi: innanzitutto l'attività solare, quindi la concentrazione dei gas presenti nell'atmosfera (e d'altra parte il rapporto tra gli isotopi di particolari gas diventa anche un indicatore dei cambiamenti climatici), in particolare i famosi gas serra, e altri elementi tra cui la potenza termica irraggiata dalla Terra.
L'importanza della potenza termica irraggiata dalla superficie terrestre è strettamente connessa con la capacità dell'atmosfera di trattenere e rimandare verso la superficie tale radiazione, cosa che è regolata dalla concentrazione dei gas serra: in parole povere, per riprendere quelle scritte da Lawrence Krauss su La fisica del cambiamento climatico, l'atmosfera è responsabile di una specie di "effetto coperta". Poiché sulla questione dell'origine dei gas serra, per ora, non voglio dilungarmi, mi è sembrato interessante proporvi il grafico della potenza termica irraggiata dalla superficie del nostro pianeta così come è stata misurata dal Clouds and the Earth's Radiant Energy System della NASA. Ovviamente, maggiore è la radiazione che viene riflessa verso il basso dall'atmosfera, e più aumenterà quella che la Terra rimanderà verso l'alto.

martedì 8 luglio 2025
Cronorifugio

Iscriviti a:
Post (Atom)