3.15: Le proprietà del #185

Come già l'anno scorso, anche quest'anno vi propongo il video dedicato alle proprietà del 185 e uscito in contemporanea con il Carnevale della Matematica #185. Buona visione!

Carnevale della Matematica #185: pi day 2025

Benvenuti all'edizione n. 185 del Carnevale della matematica, la manifestazione on-line che raccoglie i post matematici dei blogger italiani che partecipano all'iniziativa.
Oggi, tra l'altro, è un giorno speciale: il pi day, il giorno del pi greco, ovvero la Giornata internazionale della matematica. In questo giorno si organizzano molti eventi un po' in tutto il mondo, e qui trovate gli eventi italiani. Qui su questo blog, che ormai da anni ospita il Carnevale della matematica proprio in occasione del pi day, il tema portante sarà, come da tradizione, il pi greco, che sviluppo all'interno del post attraverso le notizie pi greche. Questi box, due o tre a edizione, si intercalano tra i contributi dei matematti sviluppando il tema portante, mentre nell'introduzione vado a riassumere alcune delle proprietà del numero corrispondente all'edizione. Cosa da cui non sfuggiamo nemmeno quest'anno!

Le proprietà del 185

La poesia gaussiana di Marco Fulviuo Barozzi, in arte Popinga, è una struttuta poetica generata in maniera abbastanza semplice. Partendo dal 2, il primo numero primo della lista, associa a ciascun numero primo un vorso costituito da una parola o da una combinazione di parole, mentre a ciascun verso associato a un numero non primo, i corrispondenti versi "primi" con le opportune ripetizioni in base, appunto, alla fattorizzazione di quel verso.
Questa semplice regola permette di ricavare il verso della poesia gaussiana per ciascun numero naturale, a meno di avere un verso associato a ciascun numero primo. Il problema dell'estensione originale di Popinga è che l'ultimo numero primo considerato è il 31, ma la fattorizzazione del 185, ovvero l'ordinale associato a questa edizione del Carnevale della matenatica è \[185 = 5 \times 37\] per cui per generare il verso gaussiano associato a questa edizione era necessaria un'estensione di quelli che chiamo i "versi primi", estensione che trovate su questa pagina, ma che non è di mio pugno. A partire da questa estensione, il verso gaussiano risulta quindi:

tra i cespigli gorgheggiando

Se poi facciamo la somma dei suoi divisori, otteniamo 43 che è minore di 185, il che rende quest'ultimo un numero difettivo.
Una proprietà molto interessante del 185 è, però, quella di essere un semiprimo. Un numero, infatti, appartiene a tale famiglia se può essere scritto come prodotto di due numeri primi, non necessariamente distinti. Si potrebbe allora dire di primo acchitto che tutti i numeri naturali sono semiprimi. In realtà non è così. Prendiamo il 4, la prima potenza di 2. Esso è semiprimo poiché \(4 = 2 \times 2\). Prendiamo la potenza di 2 successiva, 8. Possiamo scriverlo come prodotto di due numeri nel modo seguente \(8 = 2 \times 4 = 4 \times 2\), solo che l'unico primo è il 2 mentre il 4 non è primo, e quindi 8 non è semiprimo.
Anche il 581, ovvero il 185 scritto invertendo l'ordine delle sue cifre, è semiprimo, il che rende il 185 (e il 581) un numero omirpimes.
Il 185, poi, è un numero 20-gonale, ovvero che può essere rappresentato attraverso un poligono di 20 lati opportuno, e fa parte delle seguenti terne pitagoriche:

(57, 176, 185), (60, 175, 185), (104, 153, 185), (111, 148, 185), (185, 444, 481), (185, 672, 697), (185, 3420, 3425), (185, 17112, 17113)

E a proposito di triangoli rettangoli l'ultima curiosità su cui voglio soffermarmi prima di lasciarvi ai contributi di questa 185.ma edizione è legata alla spirale di Teodoro, così chiamata in onore del matematico greco Teodoro di Cirene, il primo a realizzarla.
Tale spirale viene costruita a partire dal triangolo rettangolo isoscele con cateti pari a 1. Sull'ipotenusa di tale triangolo, si costruisce un nuovo triangolo rettangolo, in cui un cateto è l'ipotenusa del triangolo precedente, e l'altro è un cateto sempre di lunghezza 1. A partire dal triangolo così ottenuto se ne costruisce un altro nello stesso modo. E così via. La spirale originale, che permette in questo modo di disegnare le radici quadrate dei numeri naturali, secondo quanto tramandatoci da Platone, si ferma al 16.mo triangolo e, quindi, alla radice quadrata di 17. E se portiamo la spirale fino al quarto giro troviamo proprio 185 triangoli rettangoli.

Pi day 2025: Tutti a raccolta!

Anche se un po' in ritardo rispetto a quel che avrei voluto, ecco l'annuncio ufficiale che chiama a raccolta i matematti, sia quelli soliti sia quelli che normalmente non partecipano al Carnevale della Matematica, a segnalarmi i loro articoli a tema matematico realizzati tra la metà febbraio e la metà marzo 2025. La deadline è, come sempre, il 12 marzo. Nell'e-mail vi ricordo di indicare il titolo, il link e una breve descrizione. Per il tema, ovviamente il protagonista principale è il pi greco, ma va bene qualunque altro genere di post, a patto che la matematica sia, comunque, protagonista.
Qui sotto un'immagine con l'indirizzo e-mail cui scrivermi. In alternativa potete scrivermi sia nel fediverso su mastodon.social, sia su instagram. Solito nick: ulaulaman.
Buona matematica a tutti!

3.15: Le proprietà del #176

L'addendum di quest'anno al Carnevale della Matematica #176 è, ovviamente, il video che ho pubblicato ieri in contemporanea con il post e dedicato proprio alle proprietà del 176, o almeno ad alcune di esse. Proprio come l'anno scorso, mi sembrava giusto dargli una ulteriore visibilità attraverso il post sul blog.

Carnevale della Matematica #176: Pi day!

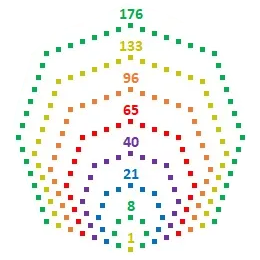
canta, canta, canta, canta all'alba

La poesia gaussiana redatta con grande impegno da Marco Fulvio Barozzi in arte Popinga è una struttura poetico-matematica abbastanza semplice da comprendere. Una volta capito come si alternano i versi si può trasformare (quasi) qualisiasi numero in un verso partendo dalla sua fattorizzazione. E per il 176, numero d'ordine del Carnevale della Matematica che vi apprestate a leggere, la sua fattorizzazione è pari a \[2^4 \times 11\] per cui dall'unione dei versi corrispondenti ai "due" fattori, ecco il verso d'apertura della special edition odierna.
Perché, come spero ricorderete (e l'orario di uscita del Carnevale è in questo un indizio significativo) oggi è il pi day, che ormai dal lontano 2012 con l'edizione #47 viene festeggiato qui su DropSea. Come è ovvio, quindi, il tema portante di questa edizione è proprio il pi greco, che sarà protagonista non solo in alcuni dei contributi che mi appresso a presentare, ma anche grazie alle ormai usuali notizie pi greche, i piccoli box con i quali nel corso degli anni ho cercato di raccontare la storia e altre curiosità del numero più famoso del mondo. Per cui questa introduzione al Carnevale è dedicata al 176.
Questi è un numero pari i cui divisori sono: 1, 2, 4, 8, 11, 16, 22, 44, 88, 176. Se li sommiamo insieme, 176 escluso, otteniamo 196, maggiore di 176, il che fa di quest'ultimo un numero abbondante. Se però alla somma di prima togliamo il 4 e il 16 otteniamo proprio 176, il che lo rende un numero semiperfetto.
Fa poi parte delle seguenti terne pitagoriche:

(57, 176, 185), (132, 176, 220), (176, 210, 274), (176, 330, 374), (176, 468, 500), (176, 693, 715), (176, 960, 976), (176, 1932, 1940), (176, 3870, 3874), (176, 7743, 7745)

proprio come il 167, ovvero il protagonista dell'edizione 2023, è un numero felice. E visto che vi voglio bene, invece di rimandarvi a quell'edizione, vi (ri)definisco qui la felicità:
Prendiamo un numero. Eleviamo al quadrato ciascuna delle sue cifre. Quindi sommiamole. Ripetiamo l'operazione con il risultato ottenuto. Proseguendo si può ricadere in due situazioni: il ciclo finisce con 1; il ciclo non finisce mai con 1 e, anzi, entra in un loop. Nel primo caso il numero si dice felice. E questa è la felicità del 176: \[1^2 + 7^2 + 6^2 = 86\] \[8^2 + 6^2 = 100\] \[1^2 = 1\] Come qualcuno avrà notato, la cosa non poteva che essere così, visto che le cifre del 176 sono una delle possibili permutazioni delle cifre del 167! Con le prossime due proprietà del 176 spero di non perdervi. Il 176, infatti, è un numero pratico. Il motivo è che tutti i numeri interi positivi precedenti al 176 possono essere scritti come somma di uno o più dei suoi divisori.
E' interessante osservare come due particolari congetture sui numeri primi, la congettura di Goldbach e la congettura dei numeri primi gemelli, che non sono ancora state dimostrate per i numeri primi, si sono rivelate vere per i numeri pratici. In pratica ogni numero pari può essere scritto come la somma di due numeri pratici, ed esistono ifniniti numeri pratici (m) tali che anche (m+2) è un numero pratico (in realtà i numeri pratici si spingono addirittura fino a terne di numeri pratici gemelli!).
Infine il 176 è un numero colombiano. Per spiegare cosa sono questi numeri faccio un esempio. Prendiamo il 43. Può essere scritto come 43 = 35 + 5 + 3. Notate che sia 5 sia 3 sono le cifre che compongono il 35. Ebbene il 43 non è un numero colombiano. Mentre, per esempio, il 42, o il nostro 176, è un numero colombiano poiché non esiste nessun intero positivo con il quale scrivere un'uguaglianza simile a quella scritta per il 43.
Lascio per ultima la proprietà che può essere rappresentata con una figura. Il 176, infatti, è un numero ottagonale poiché può essere rappresentato come un ottagono:

Pi Day 2024: Un'anteprima

Ero lì, che stavo ragionando a quale anteprima proporvi per il Carnevale della Matematica del pi day di prossima uscita (mancano ancora poche ore), con il file scritto in markdown pronto per essere convertito in html, quand'ecco che mi viene in mente che manca ancora il mio ultimo post! La corsa per aggiungerlo, integrarlo ed esportare il tutto. Un sospiro di sollievo e via, eccovi il video che è uscito ieri come anticipazione del Carnevale, e che in effetti meritava un post tutto per se:

Tutti pronti per il pi day?

Anche quest'anno la chiamata alle armi per il Carnevale della Matematica del pi day, griffato #176, arriva abbinato a un video. E come l'anno scorso, oltre a lanciare ufficialmente la raccolta dei contributi, chiedo anche a chi realizza video su YouTube (ma non solo) di segnalarmeli o tramite i commenti al video o attraverso i soliti canali, ovvero l'indirizzo e-mail o i social, in particolare mastodon e instagram che sono quelli che utilizzo di più. Quest'anno, poi, c'è anche una nuova opzione, visto che su feddit, l'alternativa italiana a reddit, è attivo un gruppo dedicato alla matematica e quindi potrete passare anche di lì per segnalare i vostri contributi o commentando sul post che spunterà a breve nel gruppo, o inserendo l'hashtag #carnevaledellamatematica: basta, però, che vi ricordiate di inserire un paio di righe di presentazione dell'articolo che mi segnalate. Deadline: 12 marzo 2024.
Non mi resta, quindi, che lasciarvi al video annuncio!

3.15: Un video addendum

Non volevo lasciare solitaria senza alcun post di appoggio la seconda uscita della mia videonewsletter, DropSea, che come il numero uno è dedicata alla matematica, in particolare proprio al pi day e al Carnevale della Matematica #167, che ovviamente continua a stare lì, a disposizione di tutti, per la consultazione, per permettere a tutti i lettori di recuperare articoli e post matematici che, speriamo, possiate trovare interessanti!
Intanto, per chi vuole, qui sotto mi potete ascoltare spiegarvi qualcosa sul Carnevale e fornire qualche anticipazione sullo stesso, anche se forse per qualcuno è ormai storia passata...

Carnevale della Matematica #167: Pi day!

il merlo tra i cespugli all'alba
canta intrepidamente
con gioia
canta il merlo, canta melodioso, canta

Questi sono i quattro versi associati ai primi quattro carnevali della matematica del 2023 della poesia gaussiana del sommo Popinga. Ho messo in grassetto il verso associato all'edizione #167, ovvero quella che vi apprestate a leggere.
E', ovviamente, un'edizione speciale, visto che oggi è il pi day, il giorno del pi greco e, per estensione, il giorno della matematica. E questa particolare edizione del Carnevale rappresenta anche qualcosa di speciale per questo blog, visto che è dal lontano 2012 con l'edizione #47 che su DropSea il 14 marzo di ogni anno stiamo festeggiando il pi day con il Carnevale della Matematica. Quindi questa è la 12.ma edizione del Carnevale del pi day ospitata da DropSea, ma soprattutto l'11.ma edizione in cui compaiono le notizie pi greche, dei piccoli box con informazioni varie sul pi greco che trovate sparse tra i contributi di queste edizione. La prima volta che queste notizie pi greche sono apparse, infatti, fu il 14 marzo del 2013 in occasione dell'edizione #59. Inizia così un secondo decennio, o un terzo lustro, fate un po' voi, di notizie pi greche. Prima però di immergerci nella lettura dei contributi pervenuti per questa edizione #167, andiamo a vedere le proprietà del 167.
Il 167 è un numero dispari, oltre che primo, proprio come il 127 che fu anche il numero associato al pi day del 2019. E come numero primo è anche un numero primo di Eisenstein, un numero primo di Chen, un numero primo sicuro e un numero primo sexy. In particolare un numero primo si dice sexy se esiste un altro numero primo distante da lui 6 unità. Si possono, quindi, definire coppie di numeri sexy, come per esempio 167 e 173. Il 167, però, appartiene anche a una terzina di numeri sexy, visto che pure il 179 è un numero primo. Ci fermiamo, però, qui, visto che il 185 non è un numero primo. Il nome sexy, però, deriva dal latino sex, ovvero 6. Che poi ci sia in giro un qualche matematico che trovi sexy questa proprietà, questi sono problemi che non attengono alla sfera della matematica.
Tornando al 167, questi oltre a essere sexy è anche un numero felice. Il motivo è semplice. Prendiamo un numero. Eleviamolo al quadrato. Prendiamo le cifre del risultato ed eleviamo al quadrato ciascuna di esse. Quindi facciamo la somma. Ripetiamo l'operazione con il risultato ottenuto. Proseguendo si può ricadere in due situazioni: il ciclo finisce con 1; il ciclo non finisce mai con 1. Nel primo caso il numero si dice felice. E questa è la felicità del 167:

\[167^2 = 27889\] \[2^2 + 7^2 + 8^2 + 8^2 + 9 = 262\] \[2^2 + 6^2 + 2^2 = 44\] \[4^2 + 4^2 = 32\] \[3^2 + 2^2 = 13\] \[1^3 + 3^2 = 10\] \[1^2 + 0^2 = 1\]

Non mi dilungo nel raccontare in maniera completa tutte le proprietà del 167 e mi limito giusto a un'ultima manciata. Iniziamo ricordando che è un numero congruente, ovvero coincide con l'area di un triangolo rettangolo che ha per lati tre numeri razionali. E' un numero omirp, ovvero 761 è anch'esso un numero primo (e anche omirp, ovviamente). Fa parte della terna pitagorica (167, 13944, 13945) e, infine, è la differenza di due quadrati:

\[167 = 84^2 - 83^2\]

Per altre curiosità sul 167 vi rimando a Prime Curios!, perché per noi è giunto il momento di immergerci tra i contributi del Carnevale della Matematica #167. Partiamo con Flavio Ubaldini, che ritroveremo nel finale con la sua cellula melodica, che ci propone la recensione che ha ricevuto il suo romanzo Il mistero della scienza infinita.

Annuncio matematico

E come ongi anni, è venuto il momento di annunciare l'edizione del piday del Carnevale della Matematica. Tra l'altro stavo guardando la lista dei Carnevali e ho notato che la prima edizione del Carnevale del piday che ho ospitato risale al 14 marzo del 2012, ormai 11 anni fa. Era il Carnevale #47. Abbiamo quindi festeggiato ben 10 piday su questo blog, e ci apprestiamo afesteggiare l'11.mo. E tutti di seguito. Quindi era un'ottima occasione per fare l'annuncio anche tramite video. Lo troverete dopo le usuali informazioni di contatto. Nel video, che fa parte della mia neonata serie delle videonewsletter, oltre a ringraziare Alberto Saracco, la cui presenza su YouTube mi ha in effetti spinto a rendere sempre più regolare il canale, segnalo anche un'altra interessante iniziativa, People for math, una playlist di video che mira a raccontare la vita di matematiche e matematici che hanno fatto grande questa disciplina. E che per quest'anno ho deciso di incorporare all'interno del Carnevale stesso!

Un ritorno carnevalesco

Mi riferisco al mio ritorno ai contributi del Carnevale della Matematica, per la precisione all'edizione #165, tenuta brillantemente in mano da Marco Fulvio Barozzi in arte Popinga (sì, lo stesso nome del famoso personaggio di Georges Simenon). E questo nonostate nell'ultimo periodo non abbia scritto poi molto dal punto di vista matematico (ma nemmeno in altri campi, a dire il vero). I contributi per la sua edizione, infatti, sono quelli con cui avrei dovuto partecipare all'edizione precedente, la #164, tenutasi a novembre (sì, c'è stato un mese di pausa... succede, a volte), e per la precisione sono:

Nella serie dei "Rompicapi di Alice" su Dropsea ecco Il cubo di Rubik, articolo su uno dei rompicapi più famosi, cui si abbina un video della serie Disney Comics&Science che può essere visto sul Caffé del Cappellaio Matto con titolo analogo: Topolino #1800: Il Cubo di Rubik. Sempre dal Caffé del Cappellaio Matto e sempre nella serie Disney Comics&Science altri due post con video questa volta entrambi dedicati agli scacchi: Scacco matto a Topolinia e Il manuale degli scacchi di Topolino.

Piccolo aneddoto: ho concluso la mia e-mail di segnalazione dei contributi a Marco con l'osservazione che, per la prossima edizione, sarei stato costretto a tornare a scrivere di matematica. Spero di riuscire a mantenere la promessa!
Ultima nota conclusiva: il Carnevale del pi day, che anche quest'anno si terrà su DropSea, torna ai numeri dispari: preparatevi! E magari iniziate amche a scriverci su qualcosa!

Carnevale della Matematica #158

E' stato un mese decisamente complicato, e siamo stati un po' distratti. Immagino che sia successo anche ad altri. - Piotr Silverbaums

Ed è di nuovo pi day, ma la situazione rispetto allo scorso anno si è, usando un eufemismo, un po' complicata. Per cui mi sono interrogato spesso sulla necessità non solo di ospitare un Carnevale della Matematica (peraltro dopo essermi preso l'impegno), ma persino un Carnevale associato con un giorno così importante e fausto come il pi day, che ricordo è anche la Giornata Internazionale della Matematica. Però, come scrivero all'inizio del mese, penso che sia importante celebrare quelle piccole cose che rendono la vita interessante, perché servono per tenerci lontani, anche solo per un po', dai cattivi pensieri.
Ed è dunque con questo spirito che do il via al Carnevale della Matematica #158 iniziando proprio dalle proprietà del numero ordinale che identifica l'edizione del 14 marzo 2022.
I suoi divisori, egli stesso incluso, sono 4: 1, 2, 79, 158. Escludendo invece il 158 dalla lista e sommando i divisori otteniamo 82 che è minore di 158 e questo lo rende un numero difettivo.
E' un numero semiprimo, poiché è il prodotto di due numeri primi, nello specifico 2 e 79. Si può essere semiprimi anche se i due numeri primi sono identici, come ad esempio avviene con 4. E' anche un numero omirpimes. A differenza di quanto potrebbe suggerire il nome, questi numeri non sono palindromi, ma, più semplicemente, se invertiamo l'ordine delle cifre otteniamo un altro numero semiprimo. Nello specifico del 158 è l'851, che è il prodotto di 23 e 37, entrambi numeri primi. E' un numero nontotiente, per la cui definizione vi rimando al Carnevale #117 e un numero congruente. Inoltre fa parte della terna pitagorica:

(158, 6240, 6242)

Infine, motivo per cui sono stato parco con le altre definizioni, è un numero di Perrin.
I numeri di Perrin sono definiti a partire dai seguenti valori \[P(0) = 3\] \[P(1) = 0\] \[P(2) = 2\] Da qui in poi la definizione è invece data da \[P(n) = P(n-2) + P(n-3)\] Ovviamente i numeri di Perrin sono i risultati di questa operazione e i primi numeri della sequenza sono

3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, ...

Potete verificare l'appartenenza del 158 alla sequenza su The on-line encyclopedia of integer sequences.
La sequenza, a quanto pare, era stata menzionata nel 1876 da Édouard Lucas, ma prende il nome dal matematico François Olivier Raoul Perrin che aveva fornito il primo riferimento esplicito nel 1899.
Cito, così di passaggio visto che mi sembra interessante, che la sequenza di Perrin può essere determinata anche usando le matrici: \[\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{pmatrix}^n \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix} = \begin{pmatrix} P\left(n\right) \\ P\left(n+1\right) \\ P\left(n+2\right) \end{pmatrix}\] Passiamo ora ai carnevalisti e a quello che ci hanno preparato per questa edizione! Iniziamo con Annalisa Santi e Il pi greco celato nel quadro di Tobia Ravà:

22022022

Nella grafia italiana delle date, ovvero giorno, mese e anno, quella di oggi è una data palindroma: 22 febbraio 2022, 22/02/2022. E mi sembrava, allora, un giorno perfetto per fare l'usuale annuncio pubblico per il Carnevale della Matematica, edizione #158, che si terrà il 14 marzo, il pi day, proprio qui su DropSea. Ovviamente si parlerà sì del pi greco, ma essendo questo il simbolo della matematica, qualunque contributo può tranquillamente essere considerato a tema. Se, dunque, avete voglia di cimentarvi nella scrittura matematica e non fate (ancora) parte del ristretto cerchio dei matematti, potete mandarmi i post che avete scritto o scriverete entro il 12 marzo al mio indirizzo e-mail, oppure usando i miei canali social, mastodon, twitter, instagram.

Stomachion #14 e #15

Scusate: settimana scorsa, rimasto profondamente colpito dalla scomparsa di Tuono Pettinato, ho rinunciato a mandare il post di segnalazione dell'uscita del nuovo numero della newsletter Stomachion. E ieri, avendo fatto uscire la newsletter sul tardi, stavo per dimenticare la stessa cosa anche con la nuova uscita. Recupero subito.
Il numero #14 era dedicato all'ultimo Carnevale della Matematica con il riassunto dei miei contributi all'edizione #151.
Il numero #15, uscito ieri, è invece dedicato alle infografiche che ho iniziato a pubblicare su EduINAF. Non ci saranno solo quelle uscite sul magazine dell'INAF, ma anche altre che ho sparso in giro per i miei blog, DropSea e Al caffè del Cappellaio Matto.

Stomachion #6: Math Edition

Ed è di nuovo tempo di Carnevale della Matematica. Questa volta, però, a ospitarlo è MaddMaths! il magazine di divulgazione matematica online del CNR diretto da Roberto Natalini. Questa nuova edizione, uscita puntualmente il 14 aprile, è la #149, che, come ci ricorda Roberto nell'introduzione, è un numero dispari, difettivo nonché il 35.mo numero primo.
Il tema dell'edizione, invece, è quello dell'Orgoglio matematico, che diventa un vero e proprio manifesto dei contributi che noi matematti abbiamo realizzato nel corso del mese precedente.
Per maggiori dettagli, trovate tutto sulla sesta uscita mia newsletter (e ovviamente iscrivetevi!). Per i più pigri metto anche il link diretto al Carnevale.

Carnevale della Matematica #148

Per il secondo anno consecutivo l'edizione del pi day del Carnevale della Matematica è rappresentata da un numero pari, il 148. Per cui un benvenuto a tutti, sempre al solito orario pi greco a tutti i nottambuli che hanno atteso la lettura puntuali alle 3:14, ma anche a quei lettori che hanno deciso di non lasciarsi travolgere dalla passione per il numero di Archimede e hanno atteso la mattina per leggere cosa i matematti hanno preparato per voi per festeggiare degnamente il pi day 2021.
Prima di immergerci tra i contributi, andiamo, come da tradizione, a riassumere alcune delle proprietà del numero di questa edizione. Come detto il 148 è un numero pari con i seguenti divisori: 1, 2, 4, 37, 74, 148. Poiché la loro somma, 148 escluso, è 118 < 148, il numero è detto difettivo.
Ha anche una caratteristica geometricamente interessante: è un numero ettagonale e 26-gonale. In generale un numero poligonale è un numero che può essere rappresentato utilizzando un poligono regolare. La regola è semplice: si prendono tanti pallini quanti sono quelli che servono per rappresentare il numero in questione e li si dispongono, riempiendo anche l'area interna, per formare un poligono regolare. Nel caso del 148 si riescono a realizzare due poligoni regolari, uno di 7 e l'altro di 26 lati.
In particolare nel caso dell'ettagono, questi ha anche un pallino al centro, rendendo il 148 un numero ettagonale centrato. Dal punto di vista matematico un numero ettagonale centrato è ricavato dalla formula \[\frac{7n^2 - 7n + 2}{2}\] Fa anche parte di ben 5 terne pitagoriche, (48, 140, 148), (111, 148, 185), (148, 1365, 1373), (148, 2736, 2740), (148, 5475, 5477), oltre a essere un numero congruente. Questo genere di numeri sono tutti naturali e sono equivalenti all'area di un triangolo rettangolo con lati razionali (ovvero costituiti da frazioni di numeri interi).
E' anche un numero di Ulam, un genere di numeri che abbiamo già incontrato in occasione del Carnevale #131, un numero odioso (ma la cosa verrà approfondita in un contributo presente nel Carnevale) ed è persino palindromo, o almeno lo è la sua rappresentazione in base 6: 404.

Vignetta di Antonino La Barbera in corso di pubblicazione su EduINAF

Annunciazione in 3.14

E sarà un altro numero pari il cardinale della prossima edizione pi greca del Carnevale della Matematica. E come al solito l'edizione del pi day, quest'anno la numero 148, si terrà sempre qui su DropSea, dopo che la numero 147 è stata, come sempre, ospitata dai Rudi Mathematici. Rispetto agli anni precedenti, però, non sono proprio sicuro di riuscire a realizzare i soliti inserti, le notizie pi greche: prometto che ci proverò, ma nel frattempo vi ripesco il video che avevo realizzato l'anno scorso sulla quadratura del cerchio:

Come al solito, se avete qualcosa da segnalarmi per il Carnevale, potete utilizzare i miei account social twitter, mastodon e instagram. Inoltre, da questa settimana, ho anche dato il via a una newsletter: iscrivetevi pure, anche perché non è detto che nelle prossime uscite non anticipi qualcosa legato al Carnevale!

Salti matematici

Per molti motivi, in particolare perché ho semplicemente dimenticato la scadenza di invio (o se preferite i molti motivi mi hanno fatto scordare la scadenza di invio) ho saltato le due ultime edizioni del Carnevale della Matematica, la #142 ospitata da Maurizio Codogno sul suo blog su Il post, e la #143 ospitata da Roberto Zanasi. E allora mi sono chiesto: alla fin fine cosa avrei proposto? Ho fatto un po' di mente locale e ho deciso di mettervi, insieme senza distinguerle, le segnalazioni matematiche che ho saltato, sperando che per la prossima edizione riesca a proporre qualcosa:

• Senza parole: un'arcotangente
• Senza parole: un'altra arcotangente
• Recensione: Darwin alla prova
• Rompicapi di Alice: Triangoli rettangoli
• Ritratti: Leonardo Fibonacci
• Particelle musicali: Lateralus
• L'uovo di Colombo astronomico

Permango ancora in una sorta di scarsa voglia di scrivere, per cui ho tirato fuori questo link post che spero possa portarvi all'attenzione qualcuna delle (spero) interessanti cose che ho scritto negli ultimi due mesi.

Carnevale della Matematica #138

E così, un anno dopo, ci troviamo di nuovo qui su DropSea per festeggiare il piday, il "giorno del pi greco". Qualcuno potrebbe obiettare che c'è ben poco da festeggiare, in questo marzo 2020, con un inizio dell'anno bersagliato dall'emergenza sanitaria dovuta al nuovo coronavirus scoperto sul finire dell'anno precedente in Cina. Mi permetto, però, di controbattere che l'idea, in fondo, è anche quella di permetterci di staccare per un po' dai problemi quotidiani e immergerci nel magico mondo della matematica. Ed è anche per questo che, quest'anno, il Carnevale del pi day ha deciso di aderire, come evento off, allo Science Web Festival (per maggiori informazioni vedete la pagina facebook e il profilo instagram) questo perchè #ladivulgazionenonsiferma.
Detto ciò, non mi resta che introdurre alle proprietà del 138, il numero di questa edizione:

A differenza degli anni passati, quest'anno ci imbattiamo in un numero pari con i seguenti divisori: 1, 2, 3, 6, 23, 46, 69. Poiché la somma dei suoi divisori è pari a 150 > 138, questi fa parte della vasta famiglia dei numeri abbondanti. A tal proposito c'è da notare che 23 + 46 + 69 = 138, il che rende il nostro numero semiperfetto.
La sua scomposizione in fattori primi è 2 $\cdot$ 3 $\cdot$ 23: essendo i tre fattori primi distinti (ovvero non avendo nessuno una potenza superiore a 1), allora 138 è anche un numero sfenico. Come il 131, è un numero di Ulam, ovvero fa parte di una successione di Ulam.
Dati i due numeri iniziali della successione, ad esempio 1 e 2, i numeri successivi sono la somma di due distinti numeri che lo precedono. Ad esempio nella successione U(1,2), quella che parte dai numeri 1 e 2, abbiamo 3 = 2+1, 4 = 3+1, 6 = 4+2 e così via.
E' anche un numero congruente, ovvero rappresenta l'area di un triangolo rettangolo con lati razionali, e, visto che siamo in argomento triangolare, fa parte delle seguenti terne pitagoriche:

(138, 184, 230), (138, 520, 538), (138, 1584, 1590), (138, 4760, 4762)

Fuori dalla matematica, si segnala la sua presenza nei cieli stellati sotto forma di una cometa, la 138P/Shoemaker-Levy, e di un asteroide, il 138 Tolosa. Inoltre NGC-138 è il codice con cui è nota una galassia a spirale (tipo la nostra Via Lattea) presente nella costellazione dei Pesci, costellazione tipicamente invernale.

Carnevale della Matematica #131

Benvenuti, grandi e piccini, al Carnevale della Matematica. Ogni mese i blogger che si occupano di matematica e sue controllate ci tengono a far conoscere urbi et orbi per il web quello che hanno scritto in materia durante il mese precedente. Così, a rotazione, il 14 di ogni mese un blogger differente ospita un ricco link post (come si diceva nel gergo "antico") con le segnalazioni degli articoli realizzati dagli altri appassionati matematti.
Come ormai avviene dal giugno 2010, più o meno ogni edizione del Carnevale propone un tema differente, che non sempre viene seguito alla lettera dai carnevalisti. A volte questo tema è esplicitamente libero, altre è sufficientemente vago da essere nella pratica libero, altre ancora è più stringente e in quel caso è anche più stimolante, risultando una sfida tra il blogger ospitante e i carnevalisti. E altre ancora, infine, ha un che di romantico, non necessariamente vincolante, ma semplicemente celebrativo, come il tema di questa 131.ma edizione: la Luna!
Il 20 luglio del 1969 il modulo lunare della missione Apollo 11 atterrava sul suolo lunare, portando per la prima volta un essere umano su un altro corpo celeste. Neil Armstrong, comandante della missione, divenne così il primo uomo a posare piede sul nostro satellite: erano le 4:56, ora italiana, del 21 luglio del 1969. Dopo Armstrong, fu la volta di Edwin Aldrin. Il grande successo di quest'ultimo, il più espansivo dell'equipaggio (in orbita intorno alla Luna, ad attenderli, c'era Michael Collins), rese popolare il suo soprannome, Buzz, tanto che Aldrin decise di adottarlo come nome ufficiale all'anagrafe! E tra una settimana saremo sempre qui, spero tutti insieme, per ricordare questo storico evento, avvenuto cinquanta anni fa. Era dunque quasi obbligatorio essere presenti anche noi matematti per partecipare alla festa, in qualche modo anticipandola, visto che oggi è il 14 luglio del 2019.
Come di consueto, però, prima di inoltrarci tra i contributi scritti dai carnevalisti nell'ultimo mese, andiamo a curiosare un po' tra le proprietà del 131, numero di questa edizione:

Il 131 è il 32° numero primo, e quindi anche un numero dispari, preceduto dal 127 e seguito dal 137. E' un numero primo permutabile, visto che sono primi sia il 113, sia il 311. E' anche un numero primo di Sophie Germain, dal nome della matematica francese che li utilizzò per dimostrare un caso particolare del famoso ultimo teorema di Fermat. Nel dettaglio un numero primo $p$ tale che $2p+1$ è anch'esso un numero primo (che nello specifico è detto numero primo sicuro), è detto numero primo di Germain. E il 131 è primo visto che $2 \cdot 131 + 1 = 263$ è anch'esso un numero primo.
Inoltre è un numero primo di Honaker, ovvero un numero primo $p_n$ tale che la somma delle cifre che compongono il numero primo è uguale alla somma delle cifre di $n$. Ad esempio $p_{32} = 131$ e $3+2=1+3+1$. E il secondo numero primo di Honaker è il 263, che è il numero primo sicuro generato dal 131 con la formula di Germain.
E' un numero primo di Eisenstein, ma quest'anno non mi dilungo nella spiegazione (per maggiori dettagli vi rimando all'introduzione del Carnevale #83), ma è il terzo numero di montagna e il primo numero primo di montagna!
In generale un numero di montagna è così fatto: la prima e l'ultima cifra del numero è 1. Le prime cifre sono in ordine crescente, le ultime in ordine decrescente. Un numero di montagna può avere al massimo una cifra più grande delle altre. La lista dei numeri di montagna è finita e l'ultimo numero è 12345678987654321. La sottolista dei numeri primi di montagna è aperta dal 131. Questa lista è costituita da 2620 termini, e questa è la fattorizzazione di 2620: \[2^2 \cdot 5 \cdot 131\] Il 131.mo numero di Fibonacci, 1066340417491710595814572169, è anche il più piccolo numero primo di Fibonacci ad avere tutte le cifre da 0 a 9.
E' la somma di tre numeri primi consecutivi, 41, 43 e 47. Inoltre è anche la somma di 31, 41 e 59 che, concatenati insieme, formano le prime 6 cifre del $\pi$.
E' un numero di Ulam generato da due numeri di Ulam consecutivi, 62 e 69. La sequenza dei numeri di Ulam, che prende nome dal fisico teorico Stanislaw Ulam che per primo la propose, è costituita da tutti i numeri interi che risultano la somma di due numeri precedenti della serie in uno e un solo modo. Si possono scrivere varie serie di numeri di Ulam a partire da una coppia di numeri distinti. Ulam propose solo la lista (1,2), generata a partire da 1 e 2. In questa lista 5 non è un numero di Ulam, poiché $5 = 3+2 = 4+1$, ovvero il 5 può essere ottenuto in due modi differenti.
Può essere scritto nella forma $2^p + 3$ con $p$ primo (nel dettaglio $p=7$). E' palindromo ed è anche il più piccolo numero primo palindromo con più di due cifre (il palindromo primo più piccolo è 11) e fa parte della terna pitagorica $(131, 8580, 8581)$.
E infine 131 è il numero della locomotiva che compare in Ritorno al futuro - Parte III.