Stomachion
sabato 30 novembre 2013
giovedì 28 novembre 2013
Fisica a colori

Indicato da Maria Popova come uno dei migliori 11 libri divulgativi scientifici del 2012, il Feynman di Jim Ottaviani e Leland Myrick è uno splendido esempio di come si possa rendere interessante la scienza. Anche con i fumetti.
Finalmente è uscita la recensione del Feynman di Ottaviani e Myrick (che come saprete sono al lavoro su Hawking): un articolo a quattro mani, scritto con Maria-Angela Silleni uscito dopo un anno e più dalla sua uscita esclusivamente per colpa mia: per molti motivi non sono riuscito a concludere in tempi brevi la mia parte del lavoro. Innanzitutto c'era da trovare la chiave migliore per inserirsi all'interno delle considerazioni che Maria-Angela mi aveva inviato, cercando magari di approfondire anche qualcosa dal punto di vista fisico. Nel complesso direi che il risultato non è male (considerate che prima della pubblicazione, ciascun articolo, dopo opportuna discussione, viene comunque riletto da un revisore, che propone comunque ulteriori spunti e suggerimenti) e, da quella recensione, estrarrei questo passaggio, che è quello con il contenuto scientifico più alto:
La QED è stata sicuramente il suo più importante e famoso contributo alla fisica e alla scienza: a esso Feynman ha dedicato, soprattutto a partire dal 1978, buona parte della sua attività didattica e divulgativa. Molti dei passaggi del libro di Ottaviani e Leyland dedicati a questa strana teoria della luce e della materia sono tratti dal libro QED, che raccoglie un ciclo di conferenze sulla materia, così come altri sono invece tratti dai Sei pezzi facili e dai Sei pezzi meno facili: ci stiamo riferendo al capitolo QED in NZ o a QED in CA, dedicati alle lezioni tenute dal fisico in Nuova Zelanda e California. In questi passaggi, inevitabilmente, l’uso delle didascalie si fa predominante, e la lettura reclama un supplemento di concentrazione, per quanto supportata dall'apparato grafico, per larga parte ripreso da quello ideato dallo stesso Feynman.
La sua collaborazione con il Progetto Manhattan, poi, è fedelmente riportata da Los Alamos dal basso, testo di una conferenza in cui il fisico ricorda quel periodo contenuto all'interno della raccolta di saggi Il piacere di scoprire, che ha il pregio di mostrare fedelmente la passione di Feynman per il gioco, la leggerezza e la scienza. E c'è, poi, il suo rivoluzionario discorso sulla miniaturizzazione, che si può leggere sempre su Il piacere di scoprire, fondamentale perché ha di fatto dato inizio alla ricerca nanotecnologica, grazie alla sfida che quel discorso aveva lanciato:
Darò mille dollari al primo che riuscirà a scrivere il contenuto della pagina di un libro in un'area venticinquemila volte più piccola (in scala lineare) in modo che sia leggibile con un microscopio elettronico.
E ne darò altri mille a chi inventerà un motore elettrico funzionante, un motore elettrico rotante che si possa manovrare dall'esterno e che non sia più grande di un cubo di 0,4 millimetri di lato, cavi esclusi.
(Richard Feynman, da C’è molto spazio là in fondo, trad. Grazia Gilberti)
La parte finale dell'articolo, con una serie di suggerimenti per l'approfondimento, diventa poi una sorta di Carnevale della Fisica non richiesto o non ufficiale, se preferite.
11 Maggio 1918: buon compleanno Dick! dei Rudi Mathematici
L'arte di Ofey di Lucia Marino
Feynman, o dell'imparare a insegnare di Amedeo Balbi
La natura non si imbroglia e Feynman e il bombardiere di Peppe Liberti
Per cui direi: leggetevelo tutto!
mercoledì 27 novembre 2013
Un romanzetto lumpen
Si stava una sera tornando dalla pizza in compagnia di un paio di amiche (che non frequentiamo più molto spesso ultimamente) e una di queste, la più giovane, commentando le voci sull'omosessualità di Tiziano Ferro (al tempo non aveva ancora fatto outing, il ragazzo) disse qualcosa del genere come indizio che doveva necessariamente confermarle, le voci:
Oltre ai due orfani, infatti, ci sono due strani soggetti, due culturisti, un bolognese e un libico, a quanto dicono, fratelli di sangue, a quanto dicono, che saranno i primi amanti della narratrice, e poi c'è Maciste, culturista e attore noto con il nome d'arte di Franco Bruno, in realtà tale Giovanni Dellacroce, ormai vecchio, stanco e cieco alla ricerca di giovani che possano soddisfare le sue naturali necessità. E Bianca, la protagonista, entra nella sua casa proprio per questo, anche se il suo vero intento è trovare la sua cassaforte per poi rapinarlo di tutti i suoi averi: è questo il crimine di cui parla all'inizio, quello che la fa sentire una criminale. E man mano che si procede nella lettura si percepisce l'assurdità del pensiero, soprattutto quando alla fine ci si rende conto che il crimine non è nemmeno avvenuto, e se c'è stato è forse molto più sottile, è più una perdita o una trasformazione, perché Bianca dall'essere una ragazza che al futuro nemmeno ci pensa, che non riesce nemmeno a immaginarlo, arriva, quel futuro, a immaginarlo, pensando a Maciste e a una vita normale insieme a lui.
E Bianca, la protagonista, entra nella sua casa proprio per questo, anche se il suo vero intento è trovare la sua cassaforte per poi rapinarlo di tutti i suoi averi: è questo il crimine di cui parla all'inizio, quello che la fa sentire una criminale. E man mano che si procede nella lettura si percepisce l'assurdità del pensiero, soprattutto quando alla fine ci si rende conto che il crimine non è nemmeno avvenuto, e se c'è stato è forse molto più sottile, è più una perdita o una trasformazione, perché Bianca dall'essere una ragazza che al futuro nemmeno ci pensa, che non riesce nemmeno a immaginarlo, arriva, quel futuro, a immaginarlo, pensando a Maciste e a una vita normale insieme a lui.
 Il romanzetto è breve e si legge velocemente, e come tutto quello che scrive Bolano si lascia leggere facilmente (lo scrittore cileno sarebbe stato in grado di trasformare in lettura appassionante anche la lista della spesa), intriso di una vena malinconica molto alla Jean Claude Izzo, molto alla Vivere stanca.
Il romanzetto è breve e si legge velocemente, e come tutto quello che scrive Bolano si lascia leggere facilmente (lo scrittore cileno sarebbe stato in grado di trasformare in lettura appassionante anche la lista della spesa), intriso di una vena malinconica molto alla Jean Claude Izzo, molto alla Vivere stanca.
Capisce troppo bene quello che sentono le ragazze per non essere omosessualeNon so se Roberto Bolano sia stato omosessuale, nella sua vita, ma certo non è da tutti riuscire a scrivere un romanzo con una protagonista femminile e per giunta in prima persona. E' praticamente l'ultimo romanzo di Bolano uscito prima della sua morte: ambientato a Roma, è la storia di una ragazza e di suo fratello, rimasti orfani dopo la morte dei genitori a causa di un incidente automobilistico. I due cercano di tirare avanti, come si suol dire, ed è proprio quel senso di pesantezza e di vuoto che sta dietro l'espressione ad essere il vero protagonista del romanzo, molto più dei protagonisti stessi, cinque personaggi che intrecciano i loro destini.
Oltre ai due orfani, infatti, ci sono due strani soggetti, due culturisti, un bolognese e un libico, a quanto dicono, fratelli di sangue, a quanto dicono, che saranno i primi amanti della narratrice, e poi c'è Maciste, culturista e attore noto con il nome d'arte di Franco Bruno, in realtà tale Giovanni Dellacroce, ormai vecchio, stanco e cieco alla ricerca di giovani che possano soddisfare le sue naturali necessità.


martedì 26 novembre 2013
Auguri Mr. Schulz
E grazie per averci lasciato le tue bellissime strisce dei peanuts, che fanno divertire e riflettere oggi come ieri, e continuerà ad essere così anche domani!
lunedì 25 novembre 2013
Mama Tandoori
Se pensate che la vostra famiglia è strana, soprattutto vostra madre, leggete questo libro e sono sicura che vi ricrederete! A meno che non troverete troppe somiglianze tra voi e loro. In questo caso avrete tutta la mia solidarietà!
In questo libro lo scrittore racconta di sè e della sua famiglia, delle dinamiche quotidiane, e dell'uso eccentrico del mattarello! Un romanzo pieno di valige, viaggi, sconti/ promozioni e tante risate!
In questo libro lo scrittore racconta di sè e della sua famiglia, delle dinamiche quotidiane, e dell'uso eccentrico del mattarello! Un romanzo pieno di valige, viaggi, sconti/ promozioni e tante risate!
venerdì 22 novembre 2013
Estratti da un viaggio cosmico
Mentre sono in procinto di partire, ecco che vi propongo degli estratti dal resoconto dell'ultima giornata di Lucca Comics & Science dedicata nel pomeriggio all'incontro con Amedeo e Rossano Piccioni, gli autori di Cosmicomic. Il resoconto è sottomesso per l'approvazione alla pubblicazione su LSB e così, nel frattempo, ho pensato bene di proporvi, in anteprima, un pezzo dell'inizio e della fine:
L'ultimo giorno di Comics&Science 2013 non è stato dedicato solo a Leo Ortolani e alla sua interrogazione degli scienziati, ma anche a un progetto particolare, soprattutto se rapportato con l'editore che lo ha proposto, la casa editrice torinese di libri scientifici Codice. Il libro in questione è Cosmicomic, un romanzo a fumetti di Amedeo Balbi, che ho rivisto con piacere dopo 4 anni, e Rossano Piccioni, dedicato, come recita il sottotitolo, agli uomini che scoprirono il Big Bang.(...)
C'è stato anche spazio per domande dal pubblico, e qui mi sono inserito prima chiedendo a Rossano quali spunti ha utilizzato per la rappresentazione della relatività spiegata da Einstein al giornalista che era andato a intervistarlo.
Ho seguito le indicazioni dello sceneggiatore, perché questa mi sembra una forma di rispetto nei confronti del suo lavoro a differenza di altri che stravolgono le sceneggiature.In effetti fa notare Amedeo quelle doppie splash page sono state particolarmente elaborate in particolare la seconda che doveva rendere il famoso esperimento mentale dell'ascensore in caduta libera (in questo caso di una stanza). In particolare, Rossano ha trovato divertente disegnare la prima delle due, quella con gli oggetti in volo.
Alla fine del'incontro alla Ubik provo a fare il bravo intervistatore e così faccio un paio di domande ad Amedeo, con il quale avevamo scambiato qualche parola poco prima dell'incontro con Leo Ortolani. Una delle prime curiosità riguarda il titolo, Cosmicomic: in effetti l'idea era quella di proporre qualcosa tipo il già citato Logicomix (si era pensato, infatti, anche a Cosmicomix) e solo incidentalmente c'è anche il leggerissimo riferimento alle Cosmicomiche di Calvino, citate da Plazzi, tra l'altro, nel corso degli incontri.
Tra l'altro, a domanda diretta, Amedeo conferma che il libro è stato proposto da lui all'editore ((devo ammettere che in quel momento la mia stima per Amedeo è cresciuta a un livello inimmaginabile: certo c'è da considerare che aveva già scritto per Codice e quindi c'era una certa fiducia reciproca, ma non è da tutti riuscire a convincere un editore di saggi a buttarsi, anche se in maniera estemporanea, sui fumetti)) che, per nostra fortuna, l'ha accettato.
La questione forse più interessante, anche per i lettori di LSB, è capire quali sono state le difficoltà tecniche che un esordiente ha dovuto affrontare:
Prima di tutto le difficoltà intrinseche nel "rendere la materia", e poi "la resa di alcune scene in particolare dove ci sono due o tre personaggi che semplicemente parlano". In questo caso "il problema è far fare qualcosa ai personaggi, senza renderli eccessivamente statici" un po' come a teatro dove si cercano delle azioni da compiere sul palco. In casi come questo "è stato bravo Rossano" (che è stato selezionato da una rosa di vari disegnatori) a sistemare gli oggetti nello spazio, ad esempio, nella spiegazione della curvatura.
Una delle scene migliori, e in questo Piccioni e Balbi sembrano concordare, è, poi, quando Humasson interagisce con un personaggio completamente inventato, che permetteva di "rappresentare il personaggio reale per quello che era: "alla mano"."
martedì 19 novembre 2013
Rappresentazione hamiltoniana
In fisica, per hamiltoniana si intende una particolare funzione (un operatore, tecnicamente) che rappresenta l'energia di un sistema. Può essere rappresentata anche graficamente: ad esempio qui sotto i punti di intersezione delle linee scure, le curve di fase, rappresentano i punti critici del sistema, ovvero quei punti dove l'equilibrio è instabile:
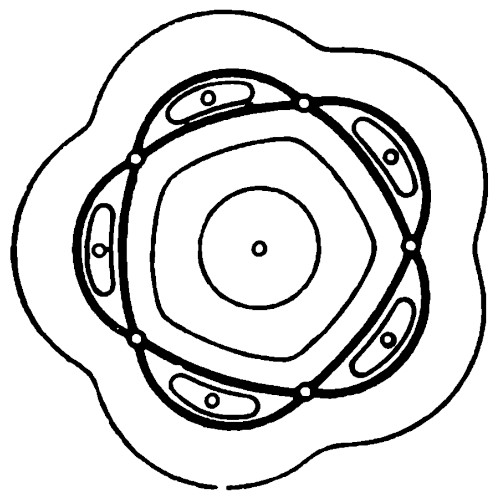 Immagine tratta da Metodi matematici della meccanica classica di Vladimir Arnol'd, Editori Riuniti, ottobre 1979.
Immagine tratta da Metodi matematici della meccanica classica di Vladimir Arnol'd, Editori Riuniti, ottobre 1979.

lunedì 18 novembre 2013
Il triangolo impossibile
Il triangolo di Penrose è stato diffuso per la prima volta nel 1958 dallo psicologo Lionel Penrose e dal figlio Roger, matematico, in un articolo che, almeno per quel che riguarda il materiale iconografico, è entrato nell'immaginario collettivo. In effetti il triangolo venne scoperto nel 1934 dall'artista svedese Oscar Reutersvärd. C'è da dire che, nonostante l'articolo abbia raggiunto comunque una certa fama, sia al momento impossibile leggerlo, a meno di non dargli una sbirciatina di traverso.
domenica 17 novembre 2013
Stephen Hawking a fumetti
A fine maggio 2010 al Teatro Franco Parenti di Milano è stata messa in scena, gratuitamente, una lettura recitata di Dio e Stephen Hawking, scritto nel 2000 da Robin Hawdon, un testo che utilizzando a pretesto la vita di Stephen Hawking, propone il tema di Dio e della creazione nel XX secolo e la sfida tra questi e in particolare tra la religione e la scienza (come scrivevo nella recensione di due anni fa). Gli elementi biografici, però, avevano comunque un certo peso e alla fine usciva fuori la figura di un uomo che troppo spesso metteva la passione per la fisica davanti agli affetti, o addirittura davanti a se stesso. Infatti sono proprio la fisica e la matematica, e il suo lavoro con Roger Penrose a spingerlo ad andare avanti nonostante la malattia degenerativa dei motoneuroni diagnosticatagli nel 1963. I successi di Hawking da allora vanno avanti di pari passo con l'aumentare delle difficoltà generate dall'avanzare della malattia e dalle difficoltà nella vita privata: a leggere teatralmente la vita del fisico, come avvenuto nel 2010, si ha la sensazione di essere di fronte a una cometa che ha cercato di bruciare le tappe, di costruire qualcosa il più velocemente possibile, prima che la malattia chiedesse il suo tributo in maniera irreversibile. In questo senso, al di là di qualunque considerazione morale sulla sua figura, Hawking è un personaggio interessantissimo, il cui carattere particolare e forse anche spigoloso non può non emergere quando si considera quanto dice Jim Ottaviani:
Per qualcuno questo può essere un atto di arroganza, ma è anche un atto di consapevolezza incredibile, sapendo perfettamente il peso mediatico della sua figura, e d'altra parte anche di grande modestia, perché questo vuol dire mettere in scena una vita complessa, ricca di soddisfazioni ma anche di cose di cui non andare proprio fieri, come la conclusione non proprio tranquilla del suo rapporto con la moglie Jane Wilde, che è coprotagonista dell'anteprima che segue.
Mentre la recensione di Feynman, scritta con Maria Angela Silleni è in attesa di pubblicazione (al momento è caricata con testo e immagini e attende l'approvazione di un qualche responsabile), gustiamoci questa anteprima diffusa da boing boing (via Hollywood Reporter):

Il 4 luglio 2012 fu un buon giorno per la fisica e per Gordy Kane, Leland e me. Non fu solo quando il bosone di Higgs venne rivelato al mondo, ma Gordy, un importante fisico e autore di The particle garden, vinse una vecchia scommessa di 100 dollari con il suo amico Stephen Hawking sul fatto che ci fosse un Higgs. E in una email inviataci per informarci riguardo queste cose, Gordy e sua moglie Lois aggiunsero anche un "Oh, a proposito..." Essi ci dissero che Stephen aveva letto e amato il nostro libro Feynman (!) e ci invitava a Cambridge per parlare riguardo un libro su di lui. Non siamo saliti su un aeroplano quello stesso pomeriggio, ma abbiamo iniziato a programmare il nostro viaggio, e questo libro. Come ho detto, un buon giorno.Già: è stato lo stesso Hawking a chiedere a due dei più famosi cartoonist scientifici di realizzare il romanzo a fumetti sulla sua vita che la First Second Books (l'editore che ha portato Gipi negli Stati Uniti) pubblicherà nel 2016.
Per qualcuno questo può essere un atto di arroganza, ma è anche un atto di consapevolezza incredibile, sapendo perfettamente il peso mediatico della sua figura, e d'altra parte anche di grande modestia, perché questo vuol dire mettere in scena una vita complessa, ricca di soddisfazioni ma anche di cose di cui non andare proprio fieri, come la conclusione non proprio tranquilla del suo rapporto con la moglie Jane Wilde, che è coprotagonista dell'anteprima che segue.
Mentre la recensione di Feynman, scritta con Maria Angela Silleni è in attesa di pubblicazione (al momento è caricata con testo e immagini e attende l'approvazione di un qualche responsabile), gustiamoci questa anteprima diffusa da boing boing (via Hollywood Reporter):

sabato 16 novembre 2013
Il teorema del ritorno di Poincaré
Prima di tutto il teorema di Liouville:
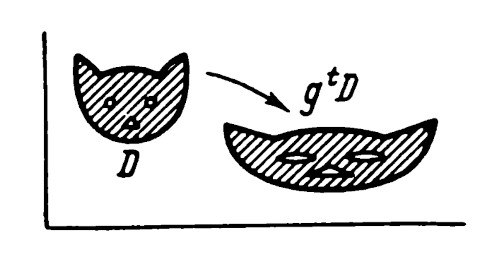 Conseguenza è che un sistema hamiltoniano stabile non può essere asintoticamente stabile(3)
Conseguenza è che un sistema hamiltoniano stabile non può essere asintoticamente stabile(3)
Il teorema del ritorno di Poincaré (anche detto della ricorrenza) quindi stabilisce che: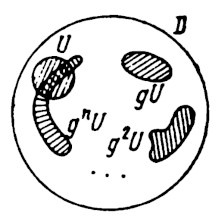
A seguito del teorema, alcuni risultati apparentemente paradossali: il primo riguarda il moto di una pallina in una buca asimmetrica: per quanto questo sia ignoto, si può star certi che prima o poi essa tornerà nelle vicinanze del punto di partenza(3):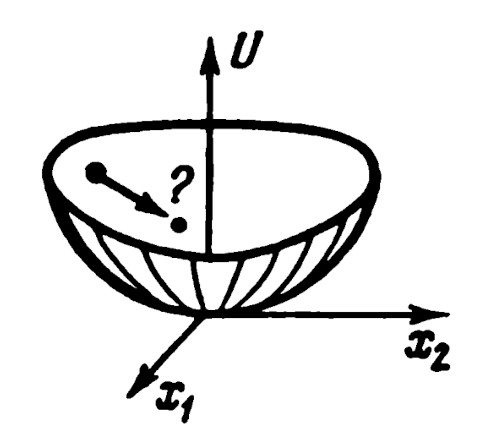 Un altro risultato paradossale, che segue alla combinazione dei due teoremi di Liouville e Poincaré, e che è intuibile già a partire dalla pallina nella buca asimmetrica, è legato alla termodinamica: se apriamo un passaggio tra due camere, una completamente vuota e una completamente piena di un qualche gas, dopo un certo tempo le molecole del gas si raccoglieranno nuovamente tutte nella prima camera(3).
Un altro risultato paradossale, che segue alla combinazione dei due teoremi di Liouville e Poincaré, e che è intuibile già a partire dalla pallina nella buca asimmetrica, è legato alla termodinamica: se apriamo un passaggio tra due camere, una completamente vuota e una completamente piena di un qualche gas, dopo un certo tempo le molecole del gas si raccoglieranno nuovamente tutte nella prima camera(3).
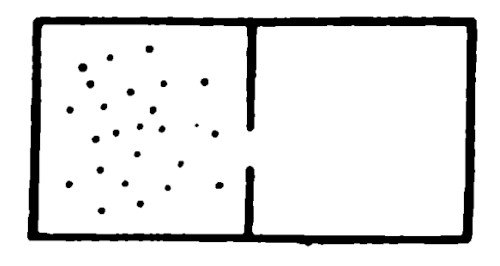
Il flusso nello spazio delle fasi, corrispondente alle equazioni di Hamilton, conserva il volume in questo spazio.(3)

Il teorema del ritorno di Poincaré (anche detto della ricorrenza) quindi stabilisce che:

Sia $g$ una trasformazione continua, biunivoca, che conservi il volume, che porti una regione limitata $D$ dello spazio euclideo in sé: $gD = D$.Questo particolare teorema scoperto dal famoso matematico francese apparve per la prima volta sul famoso articolo Sur le probléme des trois corps et les équations de la Dynamique(1) con cui Poincaré vinse il concorso indetto dal re Oscar II di Svezia, appassionato matematico, per la risoluzione di alcuni problemi di analisi.
Allora in ogni intorno $U$ di un punto qualsiasi della regione $D$ esiste un punto $x \in U$ che ritorna in $U$, cioè $g^n x \in U$, per qualche $n > 0$.(3)
A seguito del teorema, alcuni risultati apparentemente paradossali: il primo riguarda il moto di una pallina in una buca asimmetrica: per quanto questo sia ignoto, si può star certi che prima o poi essa tornerà nelle vicinanze del punto di partenza(3):


La soluzione del paradosso sta nel fatto che questo "certo tempo" è maggiore della vita del sistema solare(3).
venerdì 15 novembre 2013
Il pendolo adiabatico
In fisica, le grandezze che cambiano poco in seguito a una variazione lenta dei parametri(1) sono chiamate invarianti adiabatici. Un possibile invariante adiabatico è il pendolo. Per ottenerlo, così come per ottenere uno qualsiasi degli invarianti adiabatici, la persona, che cambia i parametri, non deve vedere in che stato si trova il sistema(1).

(1) Vladimir Igorevic Arnold, Metodi matematici della meccanica classica, Editori Riuniti, ottobre 1979.
Traduzione di Roberto Bernieri e Brunello Tirozzi

(1) Vladimir Igorevic Arnold, Metodi matematici della meccanica classica, Editori Riuniti, ottobre 1979.
Traduzione di Roberto Bernieri e Brunello Tirozzi
lunedì 11 novembre 2013
Tutto torna
Ho letto il terzo libro che mancava nella mia libreria di Giulia Carcasi, ma, dispiace ammetterlo, quello meno bello. Di facile lettura, scorrevole, si legge facilmente e velocemente. Una storia d'amore con tante sfaccettature, una storia di quotidianità e di stranezze, di grandi promesse e piccoli accorgimenti.
Ecco, il libro che mi è piaciuto di meno della Carcasi, ma non per questo non si tratta di un bel libro. Semplice, delicato, scorrevole, si potrebbe leggere in un pomeriggio uggioso, al caldo sul divano con una bella tazza di tè fumante.
Induzione
La dimostrazione per induzione si basa sul principio di induzione, secondo cui:
(...) se $\mathcal{P}$ è una proprietà che vale per $k \in \mathbb{N}$, e se $\mathcal{P}(n) \Rightarrow \mathcal{P}(n+1)$ per ogni $n \ge k$, allora $\mathcal{P}$ vale $\forall n \in \mathbb N$ con $n \ge k$.I passi su cui si basa la dimostrazione per induzione sono quindi:
In simboli: \[(\forall P)[P(0) \land ( \forall k \in \mathbb{N}) (P(k) \Rightarrow P(k+1))] \Rightarrow ( \forall n \in \mathbb{N} ) [ P(n) ] \] dove $k$ e $n$ sono numeri naturali.
- si dimostra che vale $P(1)$ (o $P(0)$), cioè che 1 (o 0) è nel sottoinsieme dei numeri naturali $U$ per cui vale $P(n)$;
- si assume come ipotesi che l'asserto $P(n)$ valga per un generico $n$ e da tale assunzione si dimostra che vale anche $P(n+1)$ (cioè che $n \in U \Rightarrow n+1 \in U$) e quindi si conclude che l'insieme $U$ dei numeri per cui vale $P(n)$ coincide con tutto l'insieme dei numeri naturali.
- Per $n=1$, $2 \geq 2$; per $n=2$, $4 \geq 4$;
- $2^{n+1} = 2 \cdot 2^n = 2^n + 2^n \geq 2n + 2n \geq 2n + 1$
venerdì 8 novembre 2013
L'universo Marvel come rete sociale

Copertina del primo numero di "Marvel Team-Up", rivista dedicata alle collaborazioni tra eroi Marvel
Investighiamo la struttura della rete di collaborazioni dell'Universo Marvel, dove due personaggi Marvel sono considerati collegati se compaiono insieme nello stesso albo Marvel. Mostriamo che questa rete non è chiaramente una rete casuale, e che ha molte, ma non tutte, le caratteristiche di una rete collaborativa "reale", come le reti collaborative degli attori cinematografici o degli scienziati. Lo studio di questo universo artificiale che cerca di apparire come vero, aiuta a comprendere che esistono dei principi di fondo che rendono le reti reali che hanno delle caratteristiche definite.(da Marvel Universe looks almost like a real social network di R. Alberich, J. Miro-Julia, F. Rossello, 2002)
giovedì 7 novembre 2013
Cedric Villani: tra manga e matematica

Parte della sua fama presso il grande pubblico è dovuta al riconoscimento ricevuto nel 2010, parte al suo bizzarro modo di vestire, quasi una sorta di cosplayer di uno dei simboli per eccellenza dell'eccentricità e della rottura delle convenzioni: Oscar Wilde.
Villani, però, è stato anche bravo a sfruttare la fama acquisita(2) per raccontare la matematica in ogni occasione concessagli.
Villani arriva leggermente in ritardo: personaggio eccentrico ed entusiasta ha fatto un giro per Lucca, in particolare presso il Japan Palace: è infatti un conoscitore e un amante di manga, che reputa una lettura molto aderente alla realtà con personaggi, vivi, ricchi di emozioni e valori morali e che in genere invecchiano nel corso della storia. In questo senso il suo punto di riferimento è Osamu Tezuka (di cui cita La storia dei tre Adolf come una delle sue preferite), su cui, insieme al manga in particolare e al fumetto in generale, si concentra la seconda metà dell'incontro delle 12:30, una vera e propria piccola conferenza sul fumetto.
Villani, dunque, spazia dalle responsabilità dei matematici nella divulgazione della loro disciplina ai modi in cui questa può essere correttamente raccontata all'interno della narrativa e del fumetto in particolare: fondamentale, dice Villani, è saper costruire una storia in grado di appassionare il lettore. Tutto ruota infatti sulle possibilità di accattivarlo e coinvolgerlo nella storia lanciandogli le giuste impressioni e sensazioni sulla matematica e soprattutto sui matematici. Come infatti sarà evidente nella presentazione pomeridiana presso la Ubik de Il teorema vivente, il primo libri divulgativo di Cedric Villani edito in Italia dalla Rizzoli, l'idea fondamentale è quella di raccontare innanzitutto i matematici.
Il progetto nasce quasi per caso: è infatti l'editore che, saputo chi è e quale sia il suo mestiere, gli chiede di scrivere un libro per la sua casa editrice. Villani, quindi, al primo incontro per discutere del progetto, gli propone qualcosa sull'entropia:
Sono un'autorità riconosciuta nel campoIl tipo però è interessato a tutt'altro: raccontare i matematici. Alla fine l'idea convince Villani che scrive così un bel libro strutturato come la storia della dimostrazione che gli ha valso la Medaglia Fields intervallata dalle storie dei matematici i cui lavori soni stati in qualche modo fondamentali per quello che si può a buon diritto chiamare come il teorema di Villani e Mouhot, il suo collaboratore per l'occasione.
E' un vero e proprio cambio di paradigma, quello di Villani, che in qualche modo segue la linea tracciata dai successi internazionali di Singh (ad esempio con A beautiful mind) o di Livio (con L'equazione impossibile). Grazie al racconto dei matematici, che in questo modo possono essere visti più da vicino dal lettore, Villani si può permettere di inserire anche gli aspetti più tecnici della matematica che se al lettore esperto trasmettono le informazioni necessarie per apprezzare al meglio il risultato raggiunto, al neofita (se non si lascia spaventare, e per certi versi distrarre dal simbolismo matematico) lasciano comunque la sensazione di una disciplina ricca e difficile ma comunque soddisfacente e appassionante oltre che comunque profondamente ancorata alla realtà.
mercoledì 6 novembre 2013
Lo faccio solo perché gentilmente richiesto...
...ma in realtà non sono in grado di poter scrivere qualcosa su 'Misterius', posso solo dire: LEGGETELO! E preparatevi a ridere come se non ci fosse un domani, perché Leo è sempre Leo!
Ci sarà qualcun altro (mio fratello) a fare una recensione seria, io non riesco, rido troppo!
Ci sarà qualcun altro (mio fratello) a fare una recensione seria, io non riesco, rido troppo!
venerdì 1 novembre 2013
In giro per Lucca 2013: tra scienza e fumetti

Venerdì 1 novembre
Incontro con Cédric Villani - ore 12.30 – Palazzo Ducale Uno dei massimi matematici viventi, vincitore della Medaglia Fields 2010, incontra il pubblico di Lucca Comics & Science e spiega perché fumetti e anime fanno parte della sua formazione. Partecipa Roberto Natalini (CNR – Roma), modera Andrea Gentile (Wired).
Presentazione de Il Teorema Vivente di Cédric Villani (Rizzoli, 2013) - ore 17.00 – Libreria Ubik (via Fillungo 137/139)
Con l’autore dialogherà Emanuele Caglioti (matematico, Università La Sapienza – Roma), conduce Stefano Pisani (giornalista scientifico, redazione Maddmaths!).
Sabato 2 novembre
“Perché l’ho fatto? Scopriamolo insieme” - ore 12.15 - Palazzo Ducale
Leo Ortolani dialoga con uomini di scienza e presenta Misterius – Speciale Scienza, la sua ultima fatica in collaborazione con lo IAC – CNR (Istituto per la Applicazioni del Calcolo “Mauro Picone”, Roma). Seguirà incontro con i lettori e seduta di autografi presso il Lucca Comics Official Stand. Partecipano Roberto Natalini (matematico – CNR, Roma), Amedeo Balbi (astrofisico – Università Tor Vergata, Roma), Ettore Perozzi ( astronomo – INAF), Ruggero Casacchia (geologo – CNR, Roma), Stefano Pisani (giornalista scientifico, redazione Maddmaths!) e Andrea Plazzi (Lucca Comics).
Un po’ di science (e comics a valanga) - ore 15.30 – Spazio Showcase
Incontro con Amedeo Balbi e Rossano Piccioni (Cosmicomic), Alessandro Lise e Alberto Talami (Le straordinarie avventure di Evariste Galois) e Sergio Ponchione, Paolo Valietti, Paolo Ubiali (Comics for Engineers). Presentano Roberto Natalini (CNR – Roma) e Andrea Plazzi (Lucca Comics).
Iscriviti a:
Post (Atom)







