Il flusso nello spazio delle fasi, corrispondente alle equazioni di Hamilton, conserva il volume in questo spazio.(3)
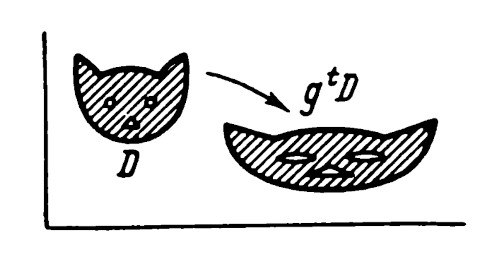
Il teorema del ritorno di Poincaré (anche detto della ricorrenza) quindi stabilisce che:
Sia $g$ una trasformazione continua, biunivoca, che conservi il volume, che porti una regione limitata $D$ dello spazio euclideo in sé: $gD = D$.Questo particolare teorema scoperto dal famoso matematico francese apparve per la prima volta sul famoso articolo Sur le probléme des trois corps et les équations de la Dynamique(1) con cui Poincaré vinse il concorso indetto dal re Oscar II di Svezia, appassionato matematico, per la risoluzione di alcuni problemi di analisi.
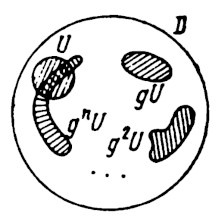
Allora in ogni intorno $U$ di un punto qualsiasi della regione $D$ esiste un punto $x \in U$ che ritorna in $U$, cioè $g^n x \in U$, per qualche $n > 0$.(3)
A seguito del teorema, alcuni risultati apparentemente paradossali: il primo riguarda il moto di una pallina in una buca asimmetrica: per quanto questo sia ignoto, si può star certi che prima o poi essa tornerà nelle vicinanze del punto di partenza(3):
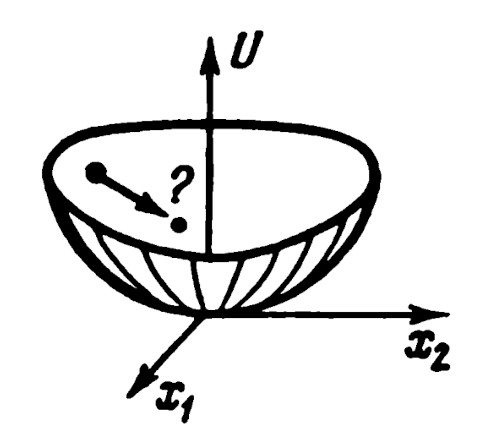
La soluzione del paradosso sta nel fatto che questo "certo tempo" è maggiore della vita del sistema solare(3).E' in un certo senso questa conseguenza che scatenò alcune polemiche Termodinamiche intorno al teorema stesso. A iniziare, infatti, fu Ernst Zermelo(2) (lo stesso dell'assioma della scelta, meglio noto come quello dei calzini!), che propose una osservazione che si poneva in aperto contrasto con l'irreversibilità e la teoria cinetica di Boltzmann:
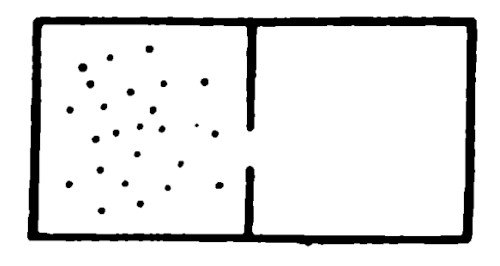
Nel secondo capitolo della memoria vincitrice di Poincaré sul problema dei tre corpi è dimostrato un teorema da cui segue che l'usuale descrizione del moto termico delle molecole, sulla quale si basa per esempio la teoria cinetica dei gas, richiede importanti modifiche al fine di risultare consistente con la legge termodinamica dell'accrescimento dell'entropia (...) In un sistema di punti materiali soggetti a forze dipendenti solo dalla posizione (...) i processi irreversibili sono impossibili dal momento che (fatta eccezione per stati iniziali singolari) nessuna funzione univoca e continua delle variabili di stato, come l'entropia, può crescere indefinitamente: se si osserva una crescita finita, ci sarà necessariamente una corrispondente decrescita non appena lo stato iniziale ricorre.(4)Fu anche Poincaré che nel 1893 osservò questa contraddizione tra la teoria cinetica e il suo teorema del ritorno(4), però, come già fatto notare anche da Boltzmann, il tempo necessario per il ritorno (ricorrenza) allo stato iniziale (o comunque a uno qualsiasi) è decisamente molto alto. Ad esempio, se si prendono le due camere dell'esempio di cui sopra, il tempo necessario al gas per ritornare nella camera iniziale è $2N \cdot \delta_\tau$, dove $N$ è il numero delle particelle di gas e $\delta_\tau \simeq h/kT$, con $h$ costante di Planck, $k$ costante di Boltzmann, $T$ temperatura. Questo tempo $\delta_\tau$ a temperatura ambiente è dell'ordine di $10^{-14}$ secondi. Se il gas è costituito da idrogeno e la camera è di circa 1 cm3, il tempo del ritorno sarà di circa $10^{-14} \cdot 10^{10^{19}}$ secondi ovvero un tempo di molto superiore all'età dell'universo che potremmo stimare come $10^{17}$ secondi(4).
L'applicabilità della teoria della probabilità ad una situazione particolare non può ovviamente essere provata matematicamente [...] ciò nonostante ogni compagnia di assicurazioni basa le sue previsioni sul calcolo delle probabilità [...] E in questo caso è ancora più valida per il numero enorme di molecole presenti un centimetro cubo di gas [...] L'assunzione che certe situazioni eccezionali non si osservino in natura non è dimostrabile in senso stretto (come non lo è l'applicabilità della stessa teoria meccanica) ma per quanto abbiamo detto è così naturale che [...] mi risulta del tutto incomprensibile il fatto che qualcuno possa vedere una confutazione dell'applicabilità della teoria della probabilità nel semplice fatto che qualche altro argomento [il teorema del ritorno] mostra che determinate eccezioni possono manifestarsi ora e poi tra un'eternità; quando poi la teoria della probabilità insegna esattamente la stessa cosa.(4)E' quasi scontato che un simile teorema non poteva non essere preda anche della meccanica quantistica, che ne propose una sua versione, che potremmo chiamare il teorema del ritorno quantistico(5):
(Ludwig Boltzmann)
Sia $\psi (t)$ una funzione d'onda che evolve nel tempo sotto l'azione dell'hamiltoniana $H$ che ha solo autovalori discreti $E_n$, con $n = 1, 2, 3, \cdots$ Allora per ogni $\epsilon$, esiste $T > 1$ tale che \[\|\psi(T) - \psi(0)\| \le \epsilon\]
(1) Poincaré H. (1890). Sur le probléme des trois corps et les équations de la dynamique, Acta Mathematica, 13 (1) A3-A270. DOI: 10.1007/BF02392506 (pdf; per approfondire: Poincaré et le problème des 3 corps)
(2) Zermelo E. (1896). Ueber einen Satz der Dynamik und die mechanische Wärmetheorie, Annalen der Physik und Chemie, 293 (3) 485-494. DOI: 10.1002/andp.18962930314
(3) Vladimir Igorevic Arnold, Metodi matematici della meccanica classica, Editori Riuniti, ottobre 1979.
Traduzione di Roberto Bernieri e Brunello Tirozzi
(4) Stefano Isola, Ricorrenza e irreversibilità (pdf)
(5) Schulman L. (1978). Note on the quantum recurrence theorem, Physical Review A, 18 (5) 2379-2380. DOI: 10.1103/PhysRevA.18.2379 (pdf)

Nessun commento:
Posta un commento