Le grandi domande della vita: Piastrellare una sfera

Una domanda interessante che ha prodotto risposte discordanti è quella relativa alla copertuna di una sfera usando dei triangoli.
La principale difficoltà nel coprire la superficie di una sfera con dei triangoli è che la superficie che vogliamo ricoprire ha una curvatura, mentre la figura che vogliamo utilizzare è piatta. QUesto vuol dire che se vogliamo utilizzare un triangolo o un qualsiasi altro poligono regolare per ricoprire la superficie di una sfera, questa figura non sarà mai identica a quella corrispondente nella usuale geometria euclidea.
Per capire la differenza, partiamo da un poligono regolare di \(n\) lati. Esso potrà essere suddiviso in altrettanti triangoli, che divideranno l'angolo al centro secondo la regola:

Cavalcare l'onda dell'asfalto

Torniamo a parlare di Formula 1, ma non dell'esito della gara di ieri (vinta da Oscar Piastri), bensì di una curva particolare del circuito di Zandvoort in Olanda, rientrato nel calendario nel 2021, dove la gara si è corsa.
La pista, riprogettata dalla ditta italiana Dromo, specializzata proprio nel design dei circuiti da corsa, ha progettato curva 3 del tracciato, nota come Hugenholtz (John Hugenholtz è stato un progettista di tracciati da corsa, tra cui Suzuka e Zolder), ispirandosi alla sequenza di Fibonacci (come ho scoperto leggendo un articolo di Federico Albano).
Ricordo che la sequenza di Fibonacci è la seguente:

Rompicapi di Alice: Un paio di giri sul treno

via pixels.com rielaborato graficamente con Canva

Il termine mathesis deriva dal greco e identificava l'imparare. Dopo la pubblicazione nel 1970 di The Order of Things del filosofo Paul-Michel Foucault, molti lo intendono come scienza universale della misura e dell'ordine, ma ai tempi di Lewis Carroll era utilizzato non solo nel significato originale, ma anche per indicare i calcoli mentali. E una delle protagoniste del terzo nodo di A tangled tale è una simpatica (ma dipende dai punti di vista!) signora della Mad Mathesis, che quindi potremmo rendere come folli calcoli mentali! E sicuramente la sfida che propone alla sua giovane ospite, la nipote Clara, sembrerebbe avere un che di folle.
Le due si trovano alla stazione di Londra, Charing Cross. Le due, in virtù di un recente completamento della linea, decidono di prendere i treni che passano per Bayswater e Birmingham e questo per un semplice motivo: viaggiano in circolo e quindi partono e arrivano a Londra senza cambiare direzione. Ovviamente i treni possono prendere due direzioni differenti, verso est e verso ovest. I tempi di percorrenza, però, sono differenti: i treni che viaggiano verso est impiegano tre ore a completare il giro, quelli che viaggiano verso ovest due ore. Nonostante questo i treni partono puntualmente ogni quarto d'ora in entrambe le direzioni.
Date queste premesse, ecco il gioco:

Matematica in vacanza #5: luglio-agosto 2025

Non c'è periodo più indicato di questo per Matematica in vacanza! E, come la puntata del mese scorso, anche in questa occasione, e nonostante la scarsezza di post squisitamente matematici, ho deciso di scorporare la parte matematica da quella più squisitamente scientifica, così domani ci sarà il solito appuntamento con Scienza take away.
Ci sbrigheremo abbastanza agilmente questo mese, visto che mancano, a differenza dello scorso anno, le recensioni dei volumi della serie Matematica uscita tra 2024 e 2025 con Corriere della Sera e Gazzetta dello Sport.
Iniziamo subito con Rompicapi e Paralipomeni di Alice. In questo periodo sto proponendo i rompicapi tratti da A tangled tale di Lewis Carroll e le ultime uscite sono state i rompicapi del secondo nodo e la loro soluzione (che in un caso differisce da quella di Carroll: chissà se avrebbe accettato la mia obiezione alla sua soluzione!).
Per la serie de Le grandi domande della vita ho affrontato, invece, uno dei problemi irrisolti della teoria dei numeri, quello della distanza razionale.
Nonostante non sia squisitamente matematica, visto che probabilmente lo avrei comunque segnalato a un eventuale Carnevale agostano, chiudo con il ritratto di Nancy Grace Roman, diventata damosa come la madre di Hubble, anche se effettivamente ha fatto molto più di questo!
Mi ritaglio, infine, uno spazietto per due segnalazioni esterne a Dropsea: un interessnate articolo sui mattoni di Mauro Merlotti e un altrettanto interessante articolo sui medici, la matematica e l'indigrazione di certi giornalisti sul ruolo della matematica nel capire come gestire le pandemie.
Prima dei saluti, semplicemente mi spiace non aver scritto di più in campo matematico, ma luglio è stato un mese piuttosto supereroico, come forse avrete letto (e se no ve lo segnalo a breve) sulla newsletter dei supereroi.

---

Immagine d'apertura generata con l'image generator di ToolBaz

Paralipomeni di Alice: Tutti in salotto!

Proseguiamo con le soluzioni tratte dai racconti matematici che costituiscono A tangled tale di Lewis Carroll. Nel secondo nodo abbiamo incontrato un rompicapo in qualche modo vacanziero: tre amici, infatti, hanno trovato 4 alloggi interessanti che si affacciano su una piazza quadrata. L'idea è scegliere uno di questi 4 alloggi come soggiorno, in particolare quello che li costringe a camminare di meno.
Per procedere con la soluzione mi sono detto: perché non utilizzare i messi moderni, come per esempio geogebra?
Ciò su cui bisogna fare maggiore attenzione è posizionare correttamente le porte, ricordando che queste sono 20 e suddividono il quadrato in 21 parti uguali. Avendo in mente ciò, e ricordando che le stanze visitate sono ai numeri 9, 25, 52 e 73, graficamente avremo una soluzione del tipo:

Rompicapi di Alice: Una piazza perfettamente quadrata

Continuo a presentarvi i rompicapi tratti da A tangled tale di Lewis Carroll con la struttura testo del rompicapo dentro i Rompicapi di Alice e soluzione dentro i Paralipomeni di Alice. Questa struttura, in effetti, è perfetta per questo periodo estivo e così, dopo il primo nodo e la sua soluzione, eccoci al secondo nodo.
I protagonisti del racconto matematico sono Balbus, Hugh e Lambert. I tre si trovano a Little Mendip, una stazione termale molto rinomata, e quindi piena di alloggi fino all'orlo, però girovagando trovano che in una piazza quadrata si trovano delle acconce dimore (in pratica dei bed&breakfast, come diremmo oggi!). La piazza è costituita da 20 palazzine per lato e ciascun lato è suddiviso in 21 parti uguali.
I tre visitano quattro stanze differenti, tutte sul retro delle case e con vista sull'orto! Le stanze visitate sono la n.9, 25, 52, 73. Balbus vuole prendere tutte e quattro le stanze, una per usarla come soggiorno e le altre tre come camere da letto. La domanda che quindi pone ai suoi giovani compagni è quindi:

Le grandi domande della vita: Il problema della distanza razionale

Una domanda interessante è chiedersi se esiste un punto all'interno di un quadrato unitario in cui le distanze dai quattro vertici sono tutte razionali. Questa è una formulazione in un certo senso semplificata del problema della distanza razionale.
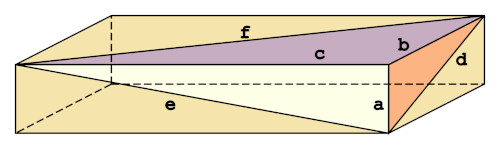
Questo è uno dei problemi irrisolti della teoria dei numeri e richiede di determinare una configurazione geometrica tale che tutte le distanze lungo specifici spigoli siano numeri razionali.

Matematica in vacanza #4: giugno-luglio 2025

(via tumblr)

Ed è venuto quel momento dell'anno in cui il Carnevale della Matematica si prende una vacanza. Così, un anno dopo aver iniziato questa serie, rieccoci qui con Matematica in vacanza per raccogliere i post matematici che ho scritto nel corso del mese precedente.
Dopo aver dato un'occhiata al terzo numero, a differenza delle edizioni precedenti, poiché la sezione non-matematica sarebbe esageratamenteo più vasta rispetto a quella matematica, ho deciso di inserire in questo link post solo quelli matematici, per quanto pochi, dandovi appuntamento a Scienza take away, che uscirà domani.

I paralipomeni di Alice: Ritorno alla locanda

Come promesso alla fine della recensione di A tangled tale di Lewis Carroll, ho iniziato a proporvi nella rubrica dei Rompicapi di Alice i quiz matematici presenti in quella raccolta. Ho iniziato con il primo nodo, proponendo il rompicapo senza alcuna soluzione. Cosa che vi propongo nel post di oggi.
Date le velocità di percorrenza ricavabili dal testo di Carroll relative ai tratti in pianura, \(s_p\), salita, \(s_s\), e discesa, \(s_d\), possiamo scrivere le equazioni che ci permettono di ricavare i tempi di percorrenza: \[t_p = \frac{s_p}{4}, \; t_s = \frac{s_s}{3}, \; t_d = \frac{s_d}{6}\] Il tempo totale, che sappiamo essere di 6 ore, è quindi dato dalla somma dei tre tempi di cui sopra: \[\frac{3 s_p + 4 s_s + 2 s_d}{12}\] Facciamo una prima semplificazione, ricordando che il tempo totale percorso dai due ospiti della locanda è \(s = s_p + s_s + s_d\), e quindi: \[\frac{3s + s_s - s_d}{12} = \frac{3s}{12} = \frac{s}{4}\] dove si ricorda che lo spazio in salita e quello in discesa sono identici e quindi si annullano.
E come detto il tempo di percorrenza è pari a 6 ore, e quindi siamo in grado di calcolare quanto i due turisti hanno percorso: 24 miglia. Che poi è proprio la soluzione indicata da Carroll nella sua rubrica.

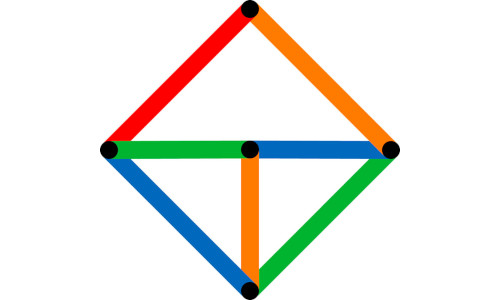
Dai tre corpi ai reticoli colorati

La storia è nota: Henri Poincaré fu il primo a "risolvere" il famoso problema dei tre corpi. E ora c'è A new proof of Poincaré's result on the restricted three-body problem, un review article, ovvero un articolo che fa il punto della situazione su un dato settore di ricerca, di Kazuyuki Yagasaki uscito sul Jounral of Mathematical Physics, protagonista di questo nuovo link post dalle riviste di ricerca.
Oltre a questo ho selezionato per segnalarveli altri tre articoli. Iniziamo con Many-body physics and resolvent algebras, che in qualche modo può essere considerato parente del paper precedente:

Some advantages of the algebraic approach to many body physics, based on resolvent algebras, are illustrated by the simple example of non-interacting bosons that are confined in compact regions with soft boundaries. It is shown that the dynamics of these systems converges to the spatially homogeneous dynamics for increasing regions and particle numbers and a variety of boundary forces. The corresponding correlation functions of thermal equilibrium states also converge in this limit. Adding to the regions further particles, the limits are steady states, including Bose–Einstein condensates. They can either be spatially homogeneous, or they are inhomogeneous with varying, but finite local particle densities. In case of this spontaneous breakdown of the spatial symmetry, the presence of condensates can be established by exhibiting temporal correlations over large temporal distances (memory effects).

Il prossimo, The asymptotic stability of solitons in the focusing Hirota equation on the line, ve lo segnalo essenzialmente perché i solitoni sono stati oggetto di "studio" (che metto tra virgolette perché è una parola grossa!) nel corso di un... corso (!) per il dottorato in fisica presso la mia università.
Infine ecco Edge coloring lattice graphs, che sembra potrebbe avere alcune applicazioni nella computazione quantistica.

I rompicapi di Alice: Una gita in montagna

Come abbiamo visto, A tangled tale di Lewis Carroll è un libro costituito da dieci rompicapi matematici originariamente proposti ai lettori di The Monthly Packet tra l'aprile del 1880 e il marzo del 1885.
Il primo di questi rompicapi, tutti scritti come dei racconti, vede due soldati fare una gita in montagna dalla locanda in cui alloggiano. Sul loro viaggio abbiamo a disposizione questi dati: la velocità in pianura è di 4 miglia orarie, quella in salita di 3 miglia orarie e quella in discesa di 6 miglia orarie. Sappiamo, inoltre, che sono partiti alle 3 del pomeriggio e dovrebbero rientrare alle 9 di sera.
Avendo a disposizione questi dati, Carroll vuole sapere quante miglia hanno percorso i due commilitoni e, come bonus, a che ora si trovavano in cima alla montagna, con un errore di mezz'ora.
Vista la semplicità della risoluzione, mi è sembrato corretto presentare questo primo rompicapo senza discuterne in questo stesso post la soluzione, lasciando il tempo a chi il libro di Carroll non l'ha letto (e quindi non conosce la soluzione) di poter provare a risolverlo. Conto di pubblicare una possibile soluzione tra un paio di settimane.

Le grandi domande della vita: La spirale di Eulero

Puntata un po' particolare della serie visto che la domanda non viene da quora ma dal passato!

---

via commons

La caratteristica principale della curva che prende il nome da Leonhard Euler è che la sua curvatura si modifica in maniera lineare con la distanza dal punto d'origine.
Fu proprio Euler a scoprirla per la prima volta in risposta a un problema sull'elasticità che gli era stato posto da Jacob Bernoulli: quale forma deve avere una molla pre-curvata in modo tale che, quando appiattita premendo sull'estremo libero, diventa una linea retta?
Euler determinò le proprietà di questa spirale nel 1744, osservando che essa possedeva due punti limite, ovvero due punti intorno ai quali si arrotolava sempre di più senza mai riuscire a raggiungerli.
In termini moderni, la curva può essere rappresentata da questa coppia di equazioni integrali:

Ritratti: Alice Lee

Alice Lee - via commons

Il Bedford College a Londra era stato fondato nel 1847 per offrire alle donne un percorso di istruzione superiore: era stato il primo istituto di tal genere nel Regno Unito. Nel 1874 il College si trasferì dalla sua sede originale in Bedford Square a York Place, vicino la famosa Baker Street, occupando due edifici. Ed è qui che nel 1876 entra come studentessa Alice Elizabeth Lee, nata il 28 giugno del 1858, figlia di William Lee, capo carrozziere, e Matilda Baker.
All'epoca a insegnare matematica c'era Percy John Harding che nei suoi primi anni non si interessò all'insegnamento della matematica a livello universitario, cosa che però sarebbe cambiata qualche anno dopo l'arrivo della Lee a Bedford. Era l'anno accademico 1879-1880 e le immatricolazioni per matematica furono 9 e di queste in testa alla graduatoria, evidentemente di merito, troviamo proprio Alice Lee, che per questo ottene un premio di 5 sterline.
La giovane si trasferì a York Place nel corso degli studi universitari, conseguendo però la laurea presso l'Università di Londra nel 1884: il motivo era perché il Bedford College non aveva lo status accademico, quindi comunque gli esami andavano sostenuti in una università vera e propria. Lee, però, non si interessava solo di scienza, e così decise di conseguire una seconda laurea, questa volta in lettere, l'anno successivo, nel 1885, sempre presso l'Università di Londra.
Subito dopo la laurea, ottenne il posto di assistente in matematica e fisica presso il Bedford College e per arrotondare il suo (magro) stipendio dava ripetizioni di greco e latino. Dal 1892 al 1894 fu assistente residente, ovvero con vitto e alloggio offerti dal College in cambio di un aiuto non-ufficiale agli studenti.

Le grandi domande della vita: Questioni di geometria

Anche se più avanti avremo alcune questioni geometriche, voglio iniziare la puntata di oggi con la risposta a una ovvietà: \[\frac{2}{\sqrt{2}} = \frac{2}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{2 \sqrt{2}}{2} = \sqrt{2}\] Ovviamente si può generalizzare la dimostrazione, ma questa cosa la lascio a chi non è andato a spulciare nel link su Quora!

Di ali che flettono

via Formula Passion

E' cosa nota dall'inizio della stagione di Formula 1 che nel Gran Premio di Barcellona, che si svolgerà proprio nel fine settimana che sta arrivando (quello dell'1 giugno) cambieranno i test di controllo sulla resistenza ai carichi delle ali davanti. Per cui può essere interessante provare a raccontare proprio la fisica delle ali di Formula 1. Iniziamo con la questione dell'attrito (che avevo affrontato alcuni anni fa nel ciclismo), che spesso viene indicato con il termine drag.
L'equazione che regola l'attrito (o resistenza all'avanzamento) è \[F_d = \frac{1}{2} \rho u^2 c_d A\] dove \(\rho\) è la densità del fluido, \(u\) la velocità dei flussi, \(c_d\) il coefficiente d'attrito, \(A\) l'area. In soldoni questa è la forza che preme su una qualsiasi ala, sia essa posteriore o anteriore, e quindi è inevitabile che generi delle deformazioni sulla stessa, flettendola in funzione dell'elasticità del materiale con cui essa è costruita.

Le grandi domande della vita: Se così, allora...

Lo so, non è esattamente un titolo che fa capire cosa ci sarà, ma non avevo molte idee quando l'ho messo giù. Per dare un'idea non solo del genere di domande affrontate, ma anche del tenore delle risposte (il più semplici possibili), partirei da una domanda a suo modo stupefacente: se \(8x = 80\), allora quanto vale \(x\)?
La risposta più ovvia è una sola e nessuno di noi farebbe nulla di più complicato di quello che vi è venuto subito in mente. Eppure delle oltre 100 risposte, la risposta più semplice, quella che vi è venuta in mente, l'ha fornita l'ai assistant di Quora...

La giostra del maleficio

La raccolta de La giostra del maleficio è costituita da 19 racconti di varia lunghezza e da un romanzo breve che la conclude. I vari racconti di Jean Ray sono tutti caratterizzati, oltre che dal tema gotico e dalla descrizione della propoensione al male, anche quello quotidiano, da parte degli esseri umani, anche da una qual certa vena di ironia. Basti pensare alla signora de La gente illustre di Tudor Street che cerca i sosia dei grandi scrittori che hanno abitato nella sua casa per usarli per riprodurre delle statue di cera di questi stessi. La fine che fanno, ovviamente, potete immaginarla, visto il titolo della raccolta!
Sono presenti, però, anche alcuni racconti che catturano in maniera altrettanto ironica una serie di spunti scientifici, come per esempio il racconto d'apertura, Matematica superiore, in cui il tema dell'omicidio si sposa con la matematica multidimensionale e la geometria non euclidea.

Il cammino di Levy

Dopo esserci occupati del cammino dell'elefante, passiamo a un altro cammino casuale, il cammino di Levy, introdotto nel 1982 da Benoît Mandelbrot e così chiamato per omaggiare il matematico francese Paul Lévy, che diede fondamentali contributi nella teoria delle probabilità. Il cammino è, in pratica, una funzione esponenziale rappresentata da una funzione del tipo:

Una storia intricata

John Fisher ne Il libro dei rompicapi di Alice, quando deve affrontare A tangled tale, un racconto ingarbugliato, scrive:

Il racconto rivela un Carroll quanto mai spiritoso, capace di combinare stuzzicanti stravaganze con la matematica rigorosa... un vero e proprio affronto ai critici che cercano di scindere la sua personalità in una identità dupolice, in cui il reverendo C. L. Dodgson non si riunì mai con il popolare autore di libri di nonsense.

L'introduzione dell'edizione di Stampa alternativa di quasi trenta anni fa (e che è rimasta non letta nella mia libreria per una quindicina d'anni, lì, in attesa, paziente), tradotta e curata da Carla Muschio, viene così introdotta dalla stessa:

Questa opera (...) è davvero anomala nella produzione di Carroll perché qui le sue due personalità, che si impegnava tanto a dividere, vengono usate insieme.

E quindi ecco trovato uno di quei critici cui si riferiva Fisher nella citazione da cui sono partito che si ritrova a curare uno dei libri dell'autore di Alice nel paese delle meraviglie. E in effetti anche io, lette quelle prime righe, ho interrotto la lettura degli articoli proposti in questa edizione. Ciò che mi stupisce, infatti, è quanto poco si conosca Lewis Carroll al di fuori dei suoi romanzi. Lo scrittore e matematico, infatti, aveva una fitta collaborazione con diverse riviste per proporre ai lettori giochi di logica e matematica, e proprio su A tangled tale sono raccolti dieci di questi racconti, originariamente apparsi su The Monthly Packet tra l'aprile del 1880 e il marzo del 1885. Vennero quindi raccolti e pubblicati in volume unico proprio in quello stesso 1885, a dicembre, corredati dalle illustrazioni di Arthur Frost.

La memoria degli elefanti

Si sa, gli elefanti sono animali dotati di grande memoria. La cosa non è semplicemente leggendaria, ma scientificamente abbastanza ben verificata, come raccontato su Focus Junior da Valentina Rorato che utilizza, come fonte primaria, un interessante articolo di ricerca del 2008: Severe drought and calf survival in elephants, articolo che in realtà cercava di determinare gli elementi che avrebbero permesso a questi grandi mammiferi di poter sopravvivere alle siccità previste causate dal riscaldamento globale.
Il punto, però, è che questa memoria leggendaria ha suggerito a Gunter Schütz e Steffen Trimper di utilizzare proprio l'elefante per introdurre un nuovo concetto in matematica: le passeggiate casuali con memoria. La proposta, che risale al 2008, prevedeva infatti che l'incremento nella passeggiata casuale dipendeva dagli incrementi precedenti, e quindi dalla "memoria" del camminatore.
Non a caso, scorrendo l'articolo, ci si ritrova di fronte a un'equazione significativa: