Le grandi domande della vita: Il problema della distanza razionale

Una domanda interessante è chiedersi se esiste un punto all'interno di un quadrato unitario in cui le distanze dai quattro vertici sono tutte razionali. Questa è una formulazione in un certo senso semplificata del problema della distanza razionale.
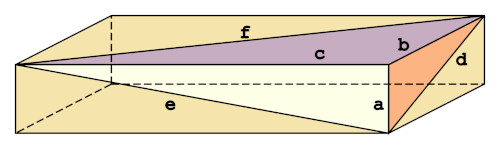
Questo è uno dei problemi irrisolti della teoria dei numeri e richiede di determinare una configurazione geometrica tale che tutte le distanze lungo specifici spigoli siano numeri razionali.
Il primo mattone per affrontare il problema è il... mattoncino di Eulero, ovvero un parallelepipedo rettangolare i cui spigoli e diagonali hanno tutti lunghezze intere. Esistono anche i mattoncini di Eulero primitivi, ovvero in cui le lunghezze degli spigoli risultano primi tra loro. Se poi in un mattoncino di Eulero la diagonale spaziale è anch'essa un numero intero, allora il mattoncino si dice perfetto, ma non è ancora stato trovato un parallelepipedo di questo tipo.
Al momento non è stata trovata alcuna soluzione per un quadrato unitario, però nel 1994 John Conway e Michael Guy hanno trovato infinite soluzioni a un suo sottoproblema, rappresentato dalla seguente equazione: \[(s^2+b^2-a^2)^2+(s^2+b^2-c^2)^2=(2bs)^2\] dove \(a\), \(b\), \(c\) sono tre distanze, mentre \(s\) è la lunghezza del lato quadrato. Esistono infinite soluzioni anche per un problema analogo con il triangolo equilatero.

Restando sui triangoli, nel 2001 è stato trovato un triangolo scaleno di lati 8, 22 e 19, il cui punto interno, come mostrato nella figura sopra, dista dai vertici 17, 6 e 4.