Quelli di autovettore e autovalore sono, infatti, due concetti matematici che hanno trovato un'utilissima applicazione nella fisica teorica. Supponiamo di avere una trasformazione lineare, che in fisica diventa una trasformazione di simmetria, ovvero una operazione che possiamo fare sullo spazio circostante come lo spostamento di un oggetto o la sua rotazione. Succederà che nel nostro spazio alcuni vettori risulteranno invariati per quel che riguarda la direzione dopo l'azione della trasformazione, ovvero la trasformazione lineare applicata sullo spazio non avrà di fatto modificato alcune porzioni dello spazio stesso. Questi vettori che non sono stati cambiati si chiamano autovettori e lo spazio da essi generato sarà detto autospazio (che ovviamente è un sottoinsieme dello spazio in cui stiamo operando). E' però possibile che la trasformazione che abbiamo applicato, pur non alterando la direzione degli autovettori, ne abbia alterato il verso (cambio di segno) o la lunghezza (cambio di modulo). Il numero che identifica questo cambiamento è detto autovalore.
Applicando questi concetti alla fisica, quando si studia un dato sistema di particelle che interagiscono tra loro, siamo in grado, con l'opportuno formalismo matematico, di determinare quali sono le trasformazioni di simmetria di quel sistema, ovvero quali operazioni lasciano invariato il sistema di particelle studiato, o di determinare anche quali parti del sistema restano invariate sotto l'azione di particolari operazioni che potremmo essere interessati ad applicare sul sistema stesso.
Con questo stesso formalismo matematico, però, possiamo anche descrivere degli oggetti fisici che non sono delle trasformazioni propriamente dette, ma che sono chiamati osservabili. Una osservabile, in fisica, è una qualunque grandezza sulla quale è possibile compiere una misura. Ad esempio la quantità di moto o la posizione o il momento angolare sono tutte osservabili fisiche. E tutte sono rappresentabili con lo stesso formalismo matematico utilizzato per le trasformazioni. Questa coincidenza è semplice da spiegare: ognuna delle osservabili fisiche citate è una grandezza vettoriale e quindi caratterizzata da una direzione e un verso e quindi da una sorta di asse di simmetria. E questo vuol dire che per ognuna delle osservabili fisiche vettoriali posso calcolare un insieme di autovettori e autovalori.

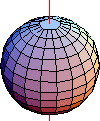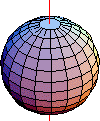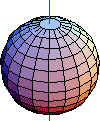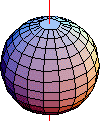
Funzioni d'onda elettroniche nell'atomo di idrogeno: sono autovettori sia dell'hamiltoniana dell'idrogeno sia del momento angolare
Questo vuol dire che, per certi versi, la teoria dei gruppi è un formalismo matematico molto più di base di quello utilizzato per lo studio delle equazioni d'onda, non necessariamente più semplice (e quindi più efficace: l'efficacia di una tecnica dipende anche da quanto si è forti nel suo utilizzo), ma ciò che è veramente interessante è che, utilizzando delle tecniche sviluppate per lo studio dell'atomo di idrogeno relativistico(1) è possibile ricavare il momento angolare e i suoi autovalori di un dato sistema fisico, come un oscillatore armonico, utilizzando delle semplici considerazioni di teoria dei gruppi(2), ovvero partendo dalle simmetrie, dagli operatori e dai commutatori, dimostrando, qualora ce ne fosse ancora bisogno, la potenza di questa tecnica di calcolo.
Approfondire:
Eigenvalues of angular momentum
Angular momentum – eigenvalues
Angular Momentum Operators
Angular momentum eigenvalues and eigenvectors (pdf)
(1) Bacry H. & Richard J.L. (1967). Partial Group-Theoretical Treatment for the Relativistic Hydrogen Atom, Journal of Mathematical Physics, 8 (11) 2230. DOI: 10.1063/1.1705146
(2) Friedmann T. & Hagen C.R. (2012). Group-theoretical derivation of angular momentum eigenvalues in spaces of arbitrary dimensions, Journal of Mathematical Physics, 53 (12) 122102. DOI: 10.1063/1.4758928 (arXiv)

Nessun commento:
Posta un commento