Iniziamo a sperimentare l'abstract da inviare solo ai lettori del feed: in questa occasione vi proporrò la versione in italiano di un recente post (sottomesso al Carnival of Mathematics) in cui tre baldi ricercatori si dedicano alla descrizione di una teoria dei grafi associata con l'arte di modellare i palloncini!
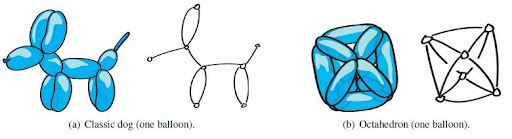
Due palloncini con accanto i grafi corrispondenti
Il lavoro, sostanzialmente, si basa sui modi possibili in cui si può modellare un palloncino. I tre ricercatori così motivano il loro lavoro:
Modellare i palloncini è divertente: l'attività può sia intrattenere sia impegnare i bambini di tutte le età. Le torsioni dei palloncini possono essere un veicolo per insegnare concetti matematici legati ai palloncini. Come vedremo, questi concetti comprendono la teoria dei grafi, gli algoritmi sui grafi, i percorsi di Eulero, il percorso del postino cinese, i poliedri (3D e 4D), i colori, le simmetrie, e anche la completezza-NP. Anche i soli modelli sono utili per l'insegnamento, ad esempio nell'illustrazione delle molecole in chimica.Ulteriore motivazione è la costruzione di strutture architettoniche con travi aeree (Army blows up building, Center manages technology of inflatable composite structures).
Il nostro approccio suggerisce che un lungo tubo a bassa pressione consente la costruzione temporanea di rifugi gonfiabili, cupole e altre strutture poliedriche, che possono essere più tardi riconfigurate in forme differenti e riutilizzate in vari luoghi. Rispetto al lavoro precedente, che disegna una struttura gonfiabile differente specificamente per ogni struttura desiderata, mostriamo la versatilità di un unico tubo.
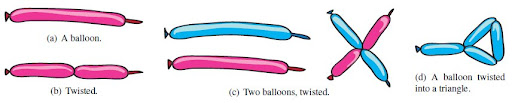 Torsione di palloncini
Torsione di palloncini
(...) un p-lone è un segmento (una linea) che può essere torto in vari punti arbitrari per formare dei vertici in cui il p-lone può essere ripiegato come una cerniera. I punti finali di un p-lone sono anch'essi dei vertici. Due vertici possono essere legati per formare dei punti di connessione permanenti. Un p-lone ritorto è stabile se ogni vertice è o legato a un altro vertice o tenuto ad un angolo di curvatura non-nullo.Si possono poi definire due modelli:
- La torsione semplice: ogni sottosegmento di un p-lone tra due vertici forma un arco nel grafo associato, che rappresenta una porzione gonfiata di un palloncino.
- Torsione pop: alcuni sotto segmenti di un p-lone tra due vertici possono essere segnate come sgonfie, non comparendo, così, nel grafo associato. Tali segmenti sgonfi possono essere ottenuti nei palloncini fisici modificando la pressione all'interno di un segmento gonfio subito accanto a quello sgonfio(1).
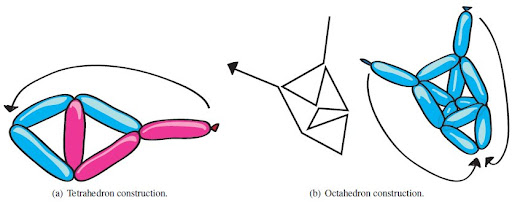
Costruzione di due solidi platonici
Th.1: Un grafo ha un numero p-lone pari a 1 se e solo se è un grafo euleriano.dove per grafo euleriano vi ricordo che si intende un grafo completamente percorribile senza passare due volte sullo stesso arco.
Th.2: Un grafo con un numero dispari o di vertici ha numero p-lone pari a o/2Nella torsione pop, ovvero, per parlar chiaro, quella che lascia la coda sgonfia in fondo (che, come vedremo nel video in fondo al post, serve per un motivo fisicamente ben preciso), il problema principale è minimizzare la lunghezza del p-lone. Tale problema è equivalente a quello del percorso del postino cinese (Nist, MathWorld), ovvero quale è il percorso più breve per consegnare la posta. Dal punto di vista della teoria dei grafi, questo problema si riduce alla ricerca di un percorso ciclico di lunghezza minima in un grafo senza orientazione. Se il grafo ha un circuito (percorso) euleriano, questo sarà una soluzione ottima al problema (Wikipedia).
All'interno di questa descrizione, detto k il numero di percorsi presenti nel p-lone, il seguente teorema risulta vero:
Th.3: Esiste un algoritmo NP che, dati un grafo e un k ≥ 1, trova i k p-loni di minima lunghezza che terminano con una coda.L'ultimo teorema riguarda il problema di Hoyler, che può essere raccontato in questi termini:
Bisogna decidere se gli archi di un grafo possono essere decomposti in copie un fissato grafo H.I tre ricercatori fanno riferimento a Krzysztof Bryś e Zbigniew Lonc che nel 2009 risolvono il problema e da qui ecco il teorema n.4:
Th.4: Ogni grafo con archi di lunghezza unitaria può essere torto per formare duoploni e possibilmente un demidouplone (quando il grafo ha un numero dispari di archi).Si può a questo punto definire un l-plone come un p-lone di lunghezza l, con l intero, avendo definito l'arco la nostra unità di misura. A questo punto ci siamo quasi: usando quest'ultimo teorema e i due successivi siamo in grado di realizzare le torsioni platoniche:
Th.5: E' NP-completo decidere se un un grafo planare bipartito con archi di lunghezza unitaria può essere torto semplicemente da un l-plone.
Th.6: E' fortemente NP-completo decidere se un grafo planare 3-connesso con o vertici dispari possa essere semplicemente torto da o/2 p-loni di uguale lunghezza.Ricordo che per problemi NP si intendono problemi risolubili in tempo polinomiale.


Palloncini platonici

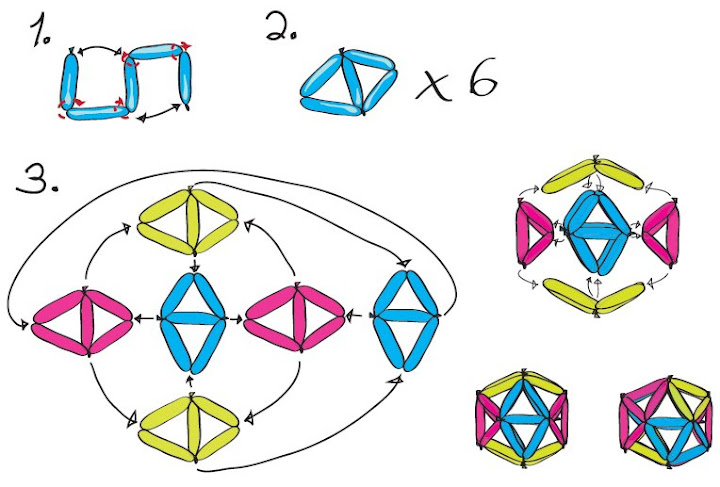
Costruzione di una bi-piramide a base triangolare

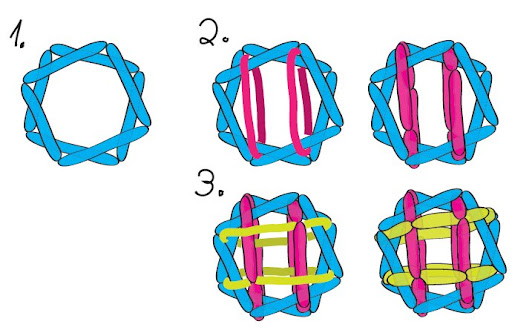
Come costruire un cubo simo
E per finire una video guida: (1) La parte specifica dell'articolo dice: by squeezing or sucking the air down the balloon or by popping a segment between two existing vertices (a practice common in balloon twisting, though requiring some care and skill). Ho deciso di renderla come nel corsivo perché mi sembrava più chiara e sintetica rispetto alla versione originale.

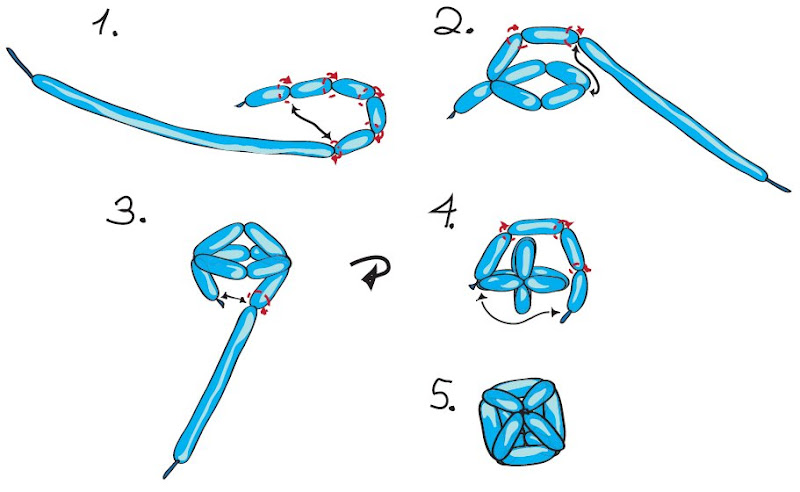
Da oggi avrò più rispetto per gli artisti di strada che fanno palloncini :)
RispondiElimina