La prima osservazione di questo effetto risale a un esperimento del 1887 di Heinrich Hertz, che ha pubblicato i risultati su Annalen der Physik(2). Il suo dispositivo era costituito da una bobina con uno spinterometro, in modo da osservare una scintilla per ogni onda elettromagnetica. Hertz pose il suo apparato in una camera oscura per vedere meglio le scintille, ma incredibilmente la massima lunghezza delle scintille prodotte era ridotta quando l'esperimento era condotto al buio. Inoltre Hertz pose un pannello di vetro tra la sorgente delle onde elettromagnetiche e lo strumento: questo pannello assorbiva la radiazione elettromagnetica che accompagnava gli elettroni nel loro salto nel buio e sostituendolo con il quarzo Hertz si aspettava che la scintilla sarebbe aumentata. Ebbene questo effetto non venne osservato, così Hertz concluse che il quarzo non aveva alcun potere di assorbimento delle radiazioni elettromagnetiche(1).
Dopo Hertz ci furono un po' di altri ricercatori che immediatamente cercarono di percorrere le orme di Hertz (tra questi anche l'italiano Augusto Righi), ma saltiamo tutti questi tentativi per andare immediatamente all'esperimento di Lenard del 1900 (i cui risultati vennero poi pubblicati nel 1902(3)). Le sue osservazioni furono stupefacenti: l'energia di uscita degli elettroni non dipendeva dall'intensità della luce incidente, ma dalla sua frequenza.
L'esperimento di Lenard è sostanzialmente costituito da due piastre metalliche, un catodo (C) e un anodo (A), poste una di fronte all'altra. Quando la radiazione elettromagnetica colpisce il catodo, questi emette degli elettroni che vanno a colpire l'anodo e permettendo così il passaggio di corrente nel circuito esterno collegato con il sistema catodo-anodo. Detta V la differenza di potenziale tra A e C, Lenard osservò che solo a partire da un certo valore, detto potenziale d'arresto, la corrente inizia a circolare, aumentando fino a raggiungere un valore massimo per poi rimanere costante. Il potenziale d'arresto è dato dall'equazione: \[\left ( \frac{1}{2} m_e v^2 \right )_{\text{max}} = e V_0\] dove $m_e$, v ed e sono rispettivamente massa, velocità e carica dell'elettrone emesso.
Ciò che Lenard, però, osservò e che ce lo fa ricordare fu un dato sorprendente: il potenziale d'arresto non dipendeva dall'intensità della luce incidente ma, come scritto, dalla sua frequenza. C'è da ricordare, in effetti, che per le conoscenze che si avevano a quel tempo, e come ho scritto in questa versione della voce wikipediana, il campo elettrico portato dalla radiazione avrebbe dovuto mettere in vibrazione gli elettroni dello strato superficiale fino a strapparli al metallo. Usciti, la loro energia cinetica sarebbe dovuta essere proporzionale all'intensità della luce incidente e non alla sua frequenza, come sembrava sperimentalmente.
Questo effetto, come ancora non poteva sapere Lenard, ma come successivamente mostrò Einstein(4), era dovuto alla nascente meccanica quantistica. Einstein, infatti, riuscì a fornire una spiegazione delle osservazioni di Lenard a partire da due lavori di Planck, uno del 1900(5) e uno del 1901(6), entrambi pubblicati sull'Annalen der Physic.
Lo spunto iniziale del lavoro di Einstein era la deduzione della impossibile catastrofe dell'ultravioletto: questo effetto catastrofico e devastante era una diretta conseguenza dello studio, tramite gli strumenti della meccanica newtoniana, della radiazione del corpo nero. Questa catastrofe, però, può essere rappresentata forse in modo più pittorico grazie al pianoforte dai tasti infiniti proposto da Gamow nei Trent'anni che sconvolsero la fisica(9):

Come ogni spiegazione teorica, però, anche questa ha bisogno di prove sperimentali solide per essere accettata completamente, e queste arrivano tra il 1914 e il 1916 quando Robert Millikan pubblicò i risultati dei suoi esperimenti sulla misura di h(7, 8):
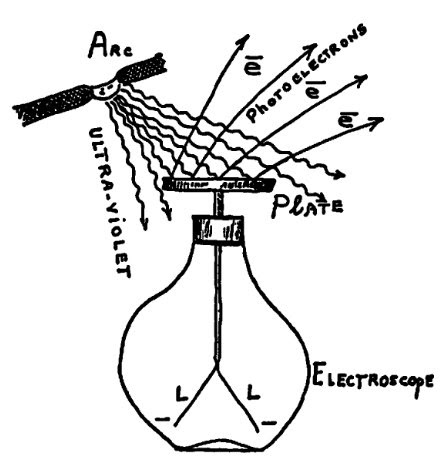
Questo metodo venne successivamente aggiornato come segue:


(2) Hertz, H. (1887). Ueber einen Einfluss des ultravioletten Lichtes auf die electrische Entladung Annalen der Physik und Chemie, 267 (8), 983-1000 DOI: 10.1002/andp.18872670827
(3) Lenard, P. (1902). Ueber die lichtelektrische Wirkung Annalen der Physik, 313 (5), 149-198 DOI: 10.1002/andp.19023130510
(4) Einstein, A. (1905). Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt Annalen der Physik, 322 (6), 132-148 DOI: 10.1002/andp.19053220607 (Wikisource)
(5) Planck, M. (1900). Ueber irreversible Strahlungsvorgänge Annalen der Physik, 306 (1), 69-122 DOI: 10.1002/andp.19003060105
(6) Planck, M. (1901). Ueber das Gesetz der Energieverteilung im Normalspectrum Annalen der Physik, 309 (3), 553-563 DOI: 10.1002/andp.19013090310
(7) Millikan, R. (1914). A Direct Determination of "h." Physical Review, 4 (1), 73-75 DOI: 10.1103/PhysRev.4.73.2
(8) Millikan, R. (1916). A Direct Photoelectric Determination of Planck's "h" Physical Review, 7 (3), 355-388 DOI: 10.1103/PhysRev.7.355 (pdf)
(9) George Gamow, I trent'anni che sconvolsero la fisica, Ed. Zanichelli, trad. Laura Felici
(10) In effetti l'equazione originale andrebbe scritta come \[e V_0 + P = \frac{R}{N} \beta \nu\] dove R è la costante di Ridbergh, N il numero di molecole in un grammo equivalente, $\beta$ la costante di Boltzman

Nessun commento:
Posta un commento