
Innanzitutto partiamo da un gas a densità uniforme. Nel modello si suppone che i cambiamenti di tipo radiativo e idrodinamico che avvengono all'interno del gas sono molto più lenti del tempo dovuto a una distribuzione di velocità maxwelliana sia per gli ioni, sia per gli elettroni. Ci si pone, poi, all'equilibrio cinetico, ovvero le temperature cinetiche $\theta$ di ioni ed elettroni sono identiche.
Per calcolare la successiva evoluzione del gas si usa le equazioni per il trasporto e il riscaldamento della materia, includendo anche termini che descrivono le proprietà radiative del plasma. I coefficienti di assorbimento ed emissione sono funzioni del numero di legami e di elettroni liberi per atomo. Le popolazioni sono poi determinate dai processi di distacco e ricombinazione, sia dovuti alle radiazioni sia dovuti agli urti. Poiché le popolazioni sono parzialmente determinate dalla radiazione, non si possono calcolare a meno di non specificare il campo della radiazione.
Nell'approssimazione nota come equilibrio locale termodinamico (local thermodynamic equilibrium - LTE), le popolazioni sono quelle che ci sarebbero se l'equilibrio termodinamico fosse alla temperatura cinetica locale $\theta$. Ciò sarebbe corretto se la radiazione fosse di tipo planckiano o se fossero dominanti i processi di collisione elettroni-ioni. Questo assunto consente di utilizzare le equazioni di Boltzman-Saha che sono funzioni solo della composizione elementare, della densità di massa e della temperatura.
Supponiamo, però, che la radiazione sia non-planckiana e che i tassi di transizione radiativa non siano inferiori a quelli collisionali. La popolazione deve allora essere trovata usando equazioni che incorporano esplicitamente l'accoppiamento con la radiazione come funzione del tempo. Ovvero queste equazioni costituiscono le equazioni non-LTE.
Questo vuol dire che proprietà come assorbimento ed emissione sono influenzate anche dai cambiamenti nella popolazione, e tutto questo può essere descritto solo con un insieme completo di equazioni che copra tutte le possibilità: è proprio per fare ciò che è stato sviluppato il modello XSNB.
(via NIF)
We present the first simultaneous observations of ion acoustic and electron plasma waves in laser-produced dense plasmas with Thomson scattering. In addition to measuring the standard plasma parameters, electron temperature and density, this novel experimental technique is shown to be a sensitive method for temporally and spatially resolved measurements of the averaged ionization stage of the plasma. Experiments with highly ionized gold plasmas clearly show that the inclusion of dielectronic recombination in radiation-hydrodynamic modeling is critically important to model cooling plasmas.(3)
The last few years have seen significant progress in constructing the atomic models required for non-local thermodynamic equilibrium (NLTE) simulations. Along with this has come an increased understanding of the requirements for accurately modeling the ionization balance, energy content and radiative properties of different atomic species for a wide range of densities and temperatures. Much of this progress is the result of a series of workshops dedicated to comparing the results from different codes and computational approaches applied to a series of test problems. The results of these workshops emphasized the importance of atomic model completeness, especially in doubly-excited states and autoionization transitions, to calculating ionization balance, and the importance of accurate, detailed atomic data to producing reliable spectra.Questi due modelli sono stati messi a confronto nel primo(7) dei due articoli del NIF, la facility sulla fusione nucleare generata da 192 fasci laser che puntano contro una cavità metallica per generare un plasma dal quale estrarre energia. La struttura geometrica di questa cavità(9) è sostanzialmente quella sviluppata da Teller e Ulam.
We describe a simple screened-hydrogenic model that calculates NLTE ionization balance with sufficient accuracy, at a low enough computational cost for routine use in radiation-hydrodynamics codes. The model incorporates term splitting, $\Delta n = 0$ transitions, and approximate UTA widths for spectral calculations, with results comparable to those of much more detailed codes. Simulations done with this model have been increasingly successful at matching experimental data for laser-driven systems and hohlraums.
Accurate and efficient atomic models are just one requirement for integrated NLTE simulations. Coupling the atomic kinetics to hydrodynamics and radiation transport constrains both discretizations and algorithms to retain energy conservation, accuracy and stability. In particular, the strong coupling between radiation and populations can require either very short time steps or significantly modified radiation transport algorithms to account for NLTE material response. Considerations such as these continue to provide challenges for NLTE simulations.(6)

I fasci [che colpiscono l'hohlraum] sono disposti in quattro coni [le zone grigie in figura] sia per l'emisfero inferiore sia per quello superiore della camera-bersaglio. I due fasci più interni sono a 23,5° e 30° rispetto alla verticale, mentre quelli più esterni sono a 44,5° e a 50°.Lo spessore dell'involucro esterno della cavità è di 25 micron, per una lunghezza di 6.4 mm con un diametro di 3,55 mm, mentre il diametro della fessura di ingresso dei laser è di 2,65 mm.

Ciò che i ricercatori del NIF hanno misurato nel primo articolo è il flusso:

Una volta selezionato il modello migliore, è stato ulteriormente testato eseguendo lo stesso tipo di misure per energie differenti:
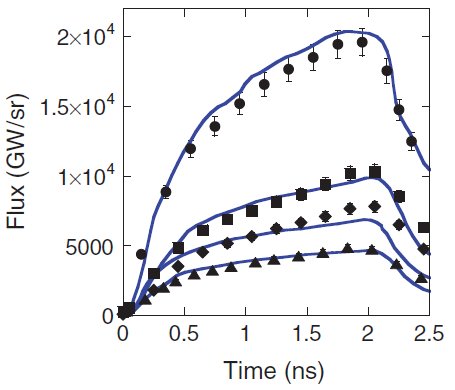
L'accordo tra le misure e le simulazioni utilizzando il modello atomico DCA con un flusso limite di 0,15 è un'indicazione che una maggiore emissività coronale del plasma conduce a plasmi più freddi che assorbono meno l'energia caratteristica e consentono soprattutto ai raggi X di riscaldare la parete. Maggiori temperature nella parete dell'hohlraum conducono a un aumento nel flusso dei raggi X misurato.L'ultimo grafico è un esame approfondito del picco osservato 2 ns nei grafici precedenti:

Nel secondo articolo(8) abbiamo, invece, le prime misure sulla potenza e la temperatura della radiazione. Gli esperimenti utilizzano del gas a una temperatura inclusa tra i 20 e 24 K(10), in capsule criogeniche contenenti elio alla densità di $8,2 \, mg \cdot cm^{-3}$. In alcune capsule ci sono anche tracce di deuterio.

Nella figura successiva, invece, il confronto tra i dati sperimentali riguardanti la temperatura della radiazione e le previsioni teoriche realizzate con il modello simulativo LASNEX(1) (la curva con la freccia verso sinistra).
Nello stesso grafico è anche mostrata, sempre in dipendenza del tempo, la potenza della radiazione X misurata sperimentalmente con Dante(4).


In conclusione: Il primo articolo mostra le prime misure sperimentali relative al flusso, selezionando anche il modello teorico migliore per l'esperimento costruito al NIF. La selezione del modello teorico inoltre conferma come la reazione all'interno della cavità sia innescata dai laser, mentre l'aumento della temperatura e quindi l'energia a disposizione viene ottenuta grazie ai raggi X generati all'interno dell'hohlraum.
Nel secondo, invece, si mostra la fattibilità del processo. I grafici dei risultati sperimentali mostrano anche dei picchi, e l'ultimo cerca di dettagliare l'andamento del picco rilevato, dimostrando così il processo di riscaldamento dell'hohlraum.
I risultati proposti sembrano convincenti e soprattutto indicano come il progetto si stia muovendo su una buona strada. Non ci resta che sperare in un loro pronto successo.
Infine un doveroso ringraziamento a Stefano Bagnasco (INFN, CICAP), Daniele Passerone (EMPA) e Charlie Osolin (NIF) che mi hanno gentilmente inviato gli articoli originali.
(1) G.B. Zimmerman, W.L. Kruer, Comments Plasma Phys. Controlled Fusion 2, 51 (1975)
(2) W.A. Lokke, W.H. Grasberger, XSNQ-U - A non-LTE emission and adsorption coefficient subroutine (1977)
(3) S.H. Glenzer et al. Thomson Scattering from High-$Z$ Laser-Produced Plasmas, Phys. Rev. Lett. 82, 97–100 (1999)
(4) E. L. Dewald et al. Dante soft x-ray power diagnostic for National Ignition Facility, Rev. Sci. Instrum. 75, 3759 (2004)
(5) K. M. Campbell et. al Omega Dante soft x-ray power diagnostic component calibration at the National Synchrotron Light Source, Rev. Sci. Instrum. 75, 3768 (2004) (6) H.A. Scott, S.B. Hansena, Advances in NLTE modeling for integrated simulations, High Energy Density Physics Volume 6, Issue 1 (2010)
(7) J.L.Kline et al. Observation of High Soft X-Ray Drive in Large-Scale Hohlraums at the National Ignition Facility, Phys. Rev. Lett. 106 (2011)
(8) S.H.Glenzer et al. Demonstration of Ignition Radiation Temperatures in Indirect-Drive Inertsial Confinement Fusion Hohlraums, Phys. Rev. Lett. 106 (2011)
(9) Il termine originale è hohlraum, parola tedesca composta da hohl e raum, spazio vuoto: un ringraziamento doveroso a mia sorella per la consulenza nella traduzione del termine.
(10) K è l'unità di misura della temperatura assoluta.
Abbiamo parlato di:
Kline, J., Glenzer, S., Olson, R., Suter, L., Widmann, K., Callahan, D., Dixit, S., Thomas, C., Hinkel, D., Williams, E., Moore, A., Celeste, J., Dewald, E., Hsing, W., Warrick, A., Atherton, J., Azevedo, S., Beeler, R., Berger, R., Conder, A., Divol, L., Haynam, C., Kalantar, D., Kauffman, R., Kyrala, G., Kilkenny, J., Liebman, J., Le Pape, S., Larson, D., Meezan, N., Michel, P., Moody, J., Rosen, M., Schneider, M., Van Wonterghem, B., Wallace, R., Young, B., Landen, O., & MacGowan, B. (2011). Observation of High Soft X-Ray Drive in Large-Scale Hohlraums at the National Ignition Facility Physical Review Letters, 106 (8) DOI: 10.1103/PhysRevLett.106.085003
Glenzer, S., MacGowan, B., Meezan, N., Adams, P., Alfonso, J., Alger, E., Alherz, Z., Alvarez, L., Alvarez, S., Amick, P., Andersson, K., Andrews, S., Antonini, G., Arnold, P., Atkinson, D., Auyang, L., Azevedo, S., Balaoing, B., Baltz, J., Barbosa, F., Bardsley, G., Barker, D., Barnes, A., Baron, A., Beeler, R., Beeman, B., Belk, L., Bell, J., Bell, P., Berger, R., Bergonia, M., Bernardez, L., Berzins, L., Bettenhausen, R., Bezerides, L., Bhandarkar, S., Bishop, C., Bond, E., Bopp, D., Borgman, J., Bower, J., Bowers, G., Bowers, M., Boyle, D., Bradley, D., Bragg, J., Braucht, J., Brinkerhoff, D., Browning, D., Brunton, G., Burkhart, S., Burns, S., Burns, K., Burr, B., Burrows, L., Butlin, R., Cahayag, N., Callahan, D., Cardinale, P., Carey, R., Carlson, J., Casey, A., Castro, C., Celeste, J., Chakicherla, A., Chambers, F., Chan, C., Chandrasekaran, H., Chang, C., Chapman, R., Charron, K., Chen, Y., Christensen, M., Churby, A., Clancy, T., Cline, B., Clowdus, L., Cocherell, D., Coffield, F., Cohen, S., Costa, R., Cox, J., Curnow, G., Dailey, M., Danforth, P., Darbee, R., Datte, P., Davis, J., Deis, G., Demaret, R., Dewald, E., Di Nicola, P., Di Nicola, J., Divol, L., Dixit, S., Dobson, D., Doppner, T., Driscoll, J., Dugorepec, J., Duncan, J., Dupuy, P., Dzenitis, E., Eckart, M., Edson, S., Edwards, G., Edwards, M., Edwards, O., Edwards, P., Ellefson, J., Ellerbee, C., Erbert, G., Estes, C., Fabyan, W., Fallejo, R., Fedorov, M., Felker, B., Fink, J., Finney, M., Finnie, L., Fischer, M., Fisher, J., Fishler, B., Florio, J., Forsman, A., Foxworthy, C., Franks, R., Frazier, T., Frieder, G., Fung, T., Gawinski, G., Gibson, C., Giraldez, E., Glenn, S., Golick, B., Gonzales, H., Gonzales, S., Gonzalez, M., Griffin, K., Grippen, J., Gross, S., Gschweng, P., Gururangan, G., Gu, K., Haan, S., Hahn, S., Haid, B., Hamblen, J., Hammel, B., Hamza, A., Hardy, D., Hart, D., Hartley, R., Haynam, C., Heestand, G., Hermann, M., Hermes, G., Hey, D., Hibbard, R., Hicks, D., Hinkel, D., Hipple, D., Hitchcock, J., Hodtwalker, D., Holder, J., Hollis, J., Holtmeier, G., Huber, S., Huey, A., Hulsey, D., Hunter, S., Huppler, T., Hutton, M., Izumi, N., Jackson, J., Jackson, M., Jancaitis, K., Jedlovec, D., Johnson, B., Johnson, M., Johnson, T., Johnston, M., Jones, O., Kalantar, D., Kamperschroer, J., Kauffman, R., Keating, G., Kegelmeyer, L., Kenitzer, S., Kimbrough, J., King, K., Kirkwood, R., Klingmann, J., Knittel, K., Kohut, T., Koka, K., Kramer, S., Krammen, J., Krauter, K., Krauter, G., Krieger, E., Kroll, J., La Fortune, K., Lagin, L., Lakamsani, V., Landen, O., Lane, S., Langdon, A., Langer, S., Lao, N., Larson, D., Latray, D., Lau, G., Le Pape, S., Lechleiter, B., Lee, Y., Lee, T., Li, J., Liebman, J., Lindl, J., Locke, S., Loey, H., London, R., Lopez, F., Lord, D., Lowe-Webb, R., Lown, J., Ludwigsen, A., Lum, N., Lyons, R., Ma, T., MacKinnon, A., Magat, M., Maloy, D., Malsbury, T., Markham, G., Marquez, R., Marsh, A., Marshall, C., Marshall, S., Maslennikov, I., Mathisen, D., Mauger, G., Mauvais, M., McBride, J., McCarville, T., McCloud, J., McGrew, A., McHale, B., MacPhee, A., Meeker, J., Merill, J., Mertens, E., Michel, P., Miller, M., Mills, T., Milovich, J., Miramontes, R., Montesanti, R., Montoya, M., Moody, J., Moody, J., Moreno, K., Morris, J., Morriston, K., Nelson, J., Neto, M., Neumann, J., Ng, E., Ngo, Q., Olejniczak, B., Olson, R., Orsi, N., Owens, M., Padilla, E., Pannell, T., Parham, T., Patterson, R., Pavel, G., Prasad, R., Pendlton, D., Penko, F., Pepmeier, B., Petersen, D., Phillips, T., Pigg, D., Piston, K., Pletcher, K., Powell, C., Radousky, H., Raimondi, B., Ralph, J., Rampke, R., Reed, R., Reid, W., Rekow, V., Reynolds, J., Rhodes, J., Richardson, M., Rinnert, R., Riordan, B., Rivenes, A., Rivera, A., Roberts, C., Robinson, J., Robinson, R., Robison, S., Rodriguez, O., Rogers, S., Rosen, M., Ross, G., Runkel, M., Runtal, A., Sacks, R., Sailors, S., Salmon, J., Salmonson, J., Saunders, R., Schaffer, J., Schindler, T., Schmitt, M., Schneider, M., Segraves, K., Shaw, M., Sheldrick, M., Shelton, R., Shiflett, M., Shiromizu, S., Shor, M., Silva, L., Silva, S., Skulina, K., Smauley, D., Smith, B., Smith, L., Solomon, A., Sommer, S., Soto, J., Spafford, N., Speck, D., Springer, P., Stadermann, M., Stanley, F., Stone, T., Stout, E., Stratton, P., Strausser, R., Suter, L., Sweet, W., Swisher, M., Tappero, J., Tassano, J., Taylor, J., Tekle, E., Thai, C., Thomas, C., Thomas, A., Throop, A., Tietbohl, G., Tillman, J., Town, R., Townsend, S., Tribbey, K., Trummer, D., Truong, J., Vaher, J., Valadez, M., Van Arsdall, P., Van Prooyen, A., Vergel de Dios, E., Vergino, M., Vernon, S., Vickers, J., Villanueva, G., Vitalich, M., Vonhof, S., Wade, F., Wallace, R., Warren, C., Warrick, A., Watkins, J., Weaver, S., Wegner, P., Weingart, M., Wen, J., White, K., Whitman, P., Widmann, K., Widmayer, C., Wilhelmsen, K., Williams, E., Williams, W., Willis, L., Wilson, E., Wilson, B., Witte, M., Work, K., Yang, P., Young, B., Youngblood, K., Zacharias, R., Zaleski, T., Zapata, P., Zhang, H., Zielinski, J., Kline, J., Kyrala, G., Niemann, C., Kilkenny, J., Nikroo, A., Van Wonterghem, B., Atherton, L., & Moses, E. (2011). Demonstration of Ignition Radiation Temperatures in Indirect-Drive Inertial Confinement Fusion Hohlraums Physical Review Letters, 106 (8) DOI: 10.1103/PhysRevLett.106.085004

Nessun commento:
Posta un commento