Dopo la recensione di Giochi matematici del medioevo, raccolta di problemi di matematica del commerciante e matematico Leonardo Fibonacci a cura di Nando Geronimi, proseguo con la serie dei Problemi di Fibonacci, parallela a quella dei Rompicapi ma destinata a una conclusione (in relazione con la fine dei giochi presenti nel libro).I problemi di oggi sono tre e sono ispirati a questo bell'articolo sull'acqua e non solo: avevo già citato questo blog sulle pagine di SciBack, ma non volevo perdere l'occasione di citare anche su queste pagine Tania e il suo lavoro. La scelta dei tre problemi è caduta sui tre legati alla fluidodinamica, anche se lo stesso Fibonacci avvisa che possono essere risolti senza alcuna necessità di usare tale branca della fisica.
Leggiamo il primo:
Il tino con quattro foriPer risolvere il problema basta ragionare in questo modo:
Un tino pieno d'acqua ha quattro rubinetti d'uscita. Usando il primo rubinetto, il tino può essere svuotato in 1 giorno; usando il secondo lo si svuota in 2 giorni; con il terzo in 3 giorni e con il quarto in 4 giorni.
In quante ore può essere svuotato il tino, se si aprono contemporaneamente i quattro rubinetti?
In un giorno il primo rubinetto svuota 1 tino, il secondo 1/2 tino, il terzo 1/3 di tino, il quarto 1/4 di tino. Sommando tutte queste frazioni otteniamo 25/12 di tino, che è il numero di tini (poco più di 2) che quei particolari 4 rubinetti riuscirebbero a svuotare lavorando contemporaneamente. Questo vuol dire che quell'unico tino verrà svuotato in 12/25 di giorno, cioè 11,52 ore, ovvero 11 ore 31 minuti e 12 secondi.
Il tino con rubinetti e foriPer risolvere quest'ultimo, invece di ragionare sul giorno, si ragiona sull'ora: quanto tino viene riempito (e svuotato) in un'ora?
Al di sopra dello stesso tino dell'esercizio precedente ci sono quattro rubinetti che portano acqua; il primo può riempire il tino in 6 ore, il secondo in 9 ore, il terzo in 24 ore e il quarto in 27 ore.
Il tino è inizialmente vuoto. Si aprono contemporaneamente i quattro rubinetti di entrata, mentre dai quattro rubinetti sul fondo continua a uscire l'acqua.
Dopo quante ore il tino sarà pieno (approssimare al minuto più vicino)?
Per quel che riguarda il primo rubinetto avremo 1/6 di tino in un'ora, e così via.
Per quel che riguarda lo svuotamento avremo che il primo rubinetto svuoterà 1/24 di tino all'ora, il secondo 1/48 e così via.
Questa seconda quantità va sottratta alla prima, e alla fine si ottengono 6 ore 28 minuti e 20 secondi(1).
Ed arriviamo, finalmente, all'ultimo problema:
La botte con fori sovrappostiPossiamo provare a farci un'idea del problema e del risultato atteso ragionando in questo modo:
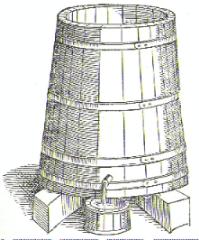
Una botte ha quattro rubinetti d'uscita, disposti uno sopra l'altro. La distanza tra due rubinetti successivi è tale da dividere la capacità della botte in quattro parti uguali. Il rubinetto più basso è sul fondo della botte.
Agendo separatamente, il rubinetto più alto svuota un quarto della botte in 1 giorno. Il secondo rubinetto svuota un quarto della botte in 2 giorni. Il terzo rubinetto svuota un quarto in 3 giorni e il rubinetto sul fondo svuota il suo quarto di botte in 4 giorni.
Se si aprono contemporaneamente i quattro rubinetti, quanto tempo occorrerà affinché la botte si svuoti? (Approssimare al secondo più vicino, senza considerare fenomeni legati alla dinamica dei fluidi).
Dopo un giorno il primo rubinetto avrà svuotato la sua porzione di botte, mentre nella porzione sopra il secondo rubinetto ci sarà meno della metà della quantità di acqua iniziale, perché nel frattempo anche gli altri due rubinetti avranno contribuito a svuotare la botte.
Il secondo giorno la seconda parte di botte sarà completamente svuotata e, mentre la quarta sarà completamente piena, la terza non lo sarà completamente, e questo vuol dire che il terzo rubinetto ci impiegherà 2 giorni e qualche ora, piuttosto che 3 giorni a svuotare la sua parte di botte.
Questo vuol dire che dopo 4 giorni all'ultimo rubinetto resterà una porzione di botte inferiore al suo quarto che, quindi svuoterà in un tempo inferiore ai 4 giorni.
Il tempo totale di svuotamento, allora sarà compreso tra i 7 e gli 8 giorni. Non a caso, considerando il giorno di 12 ore, si ottiene come risultato finale 7 giorni 1 ora 24 minuti e 30 secondi. Il modo di ragionare è il seguente:
Prendiamo una botte della capacità di 48 barili. Dal primo rubinetto l'acqua uscirà con un ritmo di 12 barili al giorno, dal secondo 6 barili al giorno, dal terzo 4 e dal quarto 3. Quindi in un giorno:
- i quattro rubinetti insieme faranno uscire 25 barili;
- i tre rubinetti inferiori fanno uscire 13 barili;
- i due rubinetti inferiori fanno uscire 7 berili;
- l'ultimo rubinetto ne fa uscire 3.
Per risolvere questo tipo di problemi è necessario conoscere la portata: \[Q = A \cdot v\] dove Q è la portata (volumetrica), A la sezione del liquido, v la sua velocità(3).
L'altra equazione di cui bisogna inevitabilmente tenere conto è l'equazione di Bernoulli: \[p + \rho \frac{v^2}{2} + \rho \cdot g \cdot h = \text{const}\]
(1) Geronimi commette un errore, trovando come risultato 4 ore e 18 minuti. L'errore sta nella somma delle frazioni di tino riempite in un'ora. Geronimi trova 69/216, mentre io 77/216.
(2) Per risolvere il problema ho ragionato in questo modo. Poniamo 1 ogni sezione, per un totale di 4. Questo vuol dire che alla fine del primo giorno l'acqua rimasta nella botte sarà:
4 - 1 - 1/2 - 1/3 - 1/4 = 1,917
che è meno della metà. Questo vuol dire che sparisce almeno un giorno, nel nostro ragionamento, visto che dopo un giorno anche la seconda sezione si è svuotata. Alla quantità restante sottraggo 1/3 e 1/4 fino a che non ottengo una quantità inferiore a 1: dopo 2 giorni si arriva a 0,75, ovvero 3/4. Questo vuol dire che ai 3 giorni fin qui trovati vanno aggiunti altri 3 giorni dovuti al solo ultimo rubinetto per un totale di 6 giorni.C'è un errore in questo ragionamento? Se sì, quale? E se no, dove sta l'errore di Fibonacci?
(3) Nell'equazione si considera la velocità di uscita perpendicolare alla sezione.
Grazie per la citazione! :-)
RispondiElimina