I rompicapi di Alice: Il conteggio di Kruskal

Prendiamo il quadrante di un orologio a lancette. Sono segnati dodici numeri, da 1 a 12. Scegliamone uno. Quindi, a partire da quello, ci spostiamo di tante posizioni quante sono le lettere della parola corrispondente a quel numero. Una volta giunti a destinazione ripetiamo l'operazione. E facciamo altrettanto la terza volta.
Su quale numero giungeremo alla fine? La risposta è sempre la stessa qualunque sia il numero di partenza: 1.

Il gioco, però, funziona solo con i nomi inglesi dei dodici numeri dell'orologio. Con i nomi in italiano le cose vanno in maniera leggermente differente. Le domande a cui rispondere sono allora: dopo quanti passi ciascuna "catena" finisce sull'1? Ed esiste un numero su cui finiscono tutte le "catene" dopo lo stesso numero di passi?
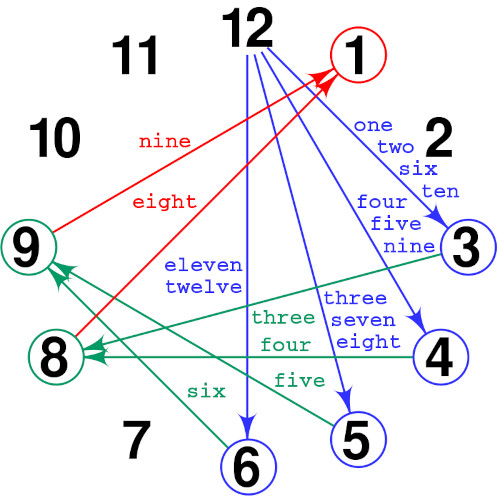
Al di là di quali siano le risposte nel caso della lingua italiana, il gioco dell'orologio descritto poc'anzi è una variazione sul Kruskal Count, gioco con le carte ideato da Martin Kruskal.

In questo caso si prende un mazzo di carte francesi e, tolti i jolly, e soprattutto dopo aver mescolato il mazzo, si dispongono le carte sul tavolo. Nel frattempo scegliamo un numero compreso tra 1 e 10. A quel punto la carta di partenza sarà quella nella posizione coincidente con il numero scelto. Il passo successivo sarà spostarsi di tante carte quante quelle corrispondenti al valore della carta. Ovviamente si ripete l'operazione su ogni carta di arrivo e questo fino a che ci sono carte nel mazzo. L'ultima carta di questa catena è quella per cui il numero di passi corrispondenti porterebbe fuori dal mazzo. Inoltre, tra le regole di spostamento, c'è quella che impone un valore di 5 a tutte le figure.
Ovviamente la nostra scelta non dobbiamo riferirla al "mago", l'altra persona con cui stiamo giocando. Quest'ultima, invece, ci dirà dove si conclude la nostra catena. E la cosa sorprendente è che, molto probabilmente, indovinerà la fine della nostra catena.
Il segreto sta nella teoria delle probabilità, in particolare nelle catene di Markov, una sequenza di eventi in cui la probabilità di un dato evento dipende dagli eventi precedenti. Come scoprì Kruskal, due catene distinte hanno una probabilità sempre più alta di finire nello stesso punto in funzione del numero di elementi totali dell'insieme. In particolare con un mazzo di 52 carte e scegliendo l'inizio della catena tra i primi dieci elementi, la catena del "mago" ha una probabilità dell'84% di concludersi nello stesso punto della nostra catena.
Il trucco venne reso popolare, come molti altri, da Martin Gardner sia sulle pagine della sua rubrica Mathematical games su Scientific American, sia sul libro Penrose Tiles to Trapdoor Ciphers (sembra che non sia stato tradotto in italiano).
Sulla questione delle probabilità, ad ogni modo, direi che potreste dare un'occhiata a Predictability Outranks Luck di Colm Mulchay, che mi sembra, tra quelli che scendono nel dettaglio, il più accessibile.

Quando segui due distinte catene di pensiero, Watson, troveriai un qualche punto di intersezione che dovrebbe approssimarsi alla verità⁽¹⁾.

- Sherlock Holmes da La scomparsa di Lady Frances Carfax nella raccolta L'ultimo saluto di Sherlock Holmes

Gardner, M. (1978). On checker jumping, the amazon game, weird dice, card tricks and other playful pastimes. Scientific American Vol. 238, No. 2, pp. 19-32 doi:10.1038/scientificamerican0278-19

---

1. When you follow two separate chains of thought, Watson, you will find some point of intersection which should approximate to the truth. ↩︎