I paralipomeni di Alice: L'orologio di Kruskal

Nel Rompicapo di Alice dedicato al Kruskal Count, gioco ideato da Martin Kruskal, avevo dedicato l'introduzione a una sua variazione, che potremmo chiamare come Kruskal Clock. Lo ripeto qui per completezza:
Prendiamo il quadrante di un orologio a lancette. Sono segnati dodici numeri, da 1 a 12. Scegliamone uno. Quindi, a partire da quello, ci spostiamo di tante posizioni quante sono le lettere della parola corrispondente a quel numero. Una volta giunti a destinazione ripetiamo l'operazione. E facciamo altrettanto la terza volta.
Se utilizziamo i nomi inglesi dei numeri, le catene giungono tutte sullo stesso numero esattamente dopo tre passaggi, ed è l'1!

I rompicapi di Alice: Il conteggio di Kruskal

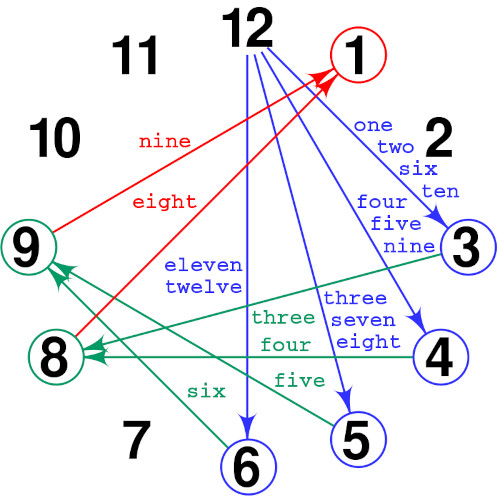
Prendiamo il quadrante di un orologio a lancette. Sono segnati dodici numeri, da 1 a 12. Scegliamone uno. Quindi, a partire da quello, ci spostiamo di tante posizioni quante sono le lettere della parola corrispondente a quel numero. Una volta giunti a destinazione ripetiamo l'operazione. E facciamo altrettanto la terza volta.
Su quale numero giungeremo alla fine? La risposta è sempre la stessa qualunque sia il numero di partenza: 1.

Il gioco, però, funziona solo con i nomi inglesi dei dodici numeri dell'orologio. Con i nomi in italiano le cose vanno in maniera leggermente differente. Le domande a cui rispondere sono allora: dopo quanti passi ciascuna "catena" finisce sull'1? Ed esiste un numero su cui finiscono tutte le "catene" dopo lo stesso numero di passi?
Al di là di quali siano le risposte nel caso della lingua italiana, il gioco dell'orologio descritto poc'anzi è una variazione sul Kruskal Count, gioco con le carte ideato da Martin Kruskal.

Ritratti: Martin David Kruskal

A parte gli argomenti su cui ho lavorato direttamente (alcuni con pochi frutti, purtroppo) una delle "curiosità" fisiche a cui mi sono avvicinato durante gli anni di dottorato è stata il concetto del solitone, ovvero un'onda solitaria ad esempio in grado di risalire la corrente dell'Union Canal in Scozia. E' stato proprio su quel canale che il solitone venne osservato per la prima volta nel 1834 dall'ingegnere John Scott Russell:

Stavo osservando il moto di una barca che veniva rapidamente trascinata da una coppia di cavalli lungo uno stretto canale, quando la barca si fermò improvvisamente, ma non così la massa d'acqua nel canale che aveva messo in moto; si accumulò intorno alla prua del vascello in uno stato di violenta agitazione, quindi allontanandosi immediatamente, rotolò in avanti con grande velocità, assumendo la forma di una larga vetta solitaria, un mucchio d'acqua arrotondato, liscio e ben definito, che continuò la sua corsa lungo il canale apparentemente senga cambiare forma o diminuire velocità. La seguii a cavallo, e la raggiunsi mentre stava ancora rotolando a circa 8 o 9 miglia all'ora, conservando la sua forma originale lunga all'incirca 30 piedi e alta tra un piede e un piede e mezzo. La sua altezza diminuì gradualmente, e dopo un inseguimento di una o due miglia la persi tra le curve del canale. Tale, nel mese di agosto del 1834, fu il mio primo casuale incontro con quel singolare e bellissimo fenomeno che ho chiamato onda di traslazione⁽¹⁾.

Per fornire una comprensione teorica del fenomeno osservato da Russell (e a cui molti guardavano con scetticismo, visto che non era previsto dai modelli all'epoca in voga) bisogna attendere gli anni Sessanta del XX secolo e il contributo del matematico e fisico Martin David Kruskal.