I paralipomeni di Alice: L'orologio di Kruskal

Nel Rompicapo di Alice dedicato al Kruskal Count, gioco ideato da Martin Kruskal, avevo dedicato l'introduzione a una sua variazione, che potremmo chiamare come Kruskal Clock. Lo ripeto qui per completezza:
Prendiamo il quadrante di un orologio a lancette. Sono segnati dodici numeri, da 1 a 12. Scegliamone uno. Quindi, a partire da quello, ci spostiamo di tante posizioni quante sono le lettere della parola corrispondente a quel numero. Una volta giunti a destinazione ripetiamo l'operazione. E facciamo altrettanto la terza volta.
Se utilizziamo i nomi inglesi dei numeri, le catene giungono tutte sullo stesso numero esattamente dopo tre passaggi, ed è l'1!

La spiegazione del fenomeno è la stessa dietro il Kruskal Count, per cui non aggiungo altro oltre quello già scritto nel Rompicapo precedentemente citato, però in questo Paralipomeno mi dedico alla risposta al quesito che avevo posto all'inizio: cosa succede se usiamo, invece, i nomi in italiano? Innanzitutto associamo ad ogni numero la corrispondente quantità di passi da compiere per spostarsi lungo l'orologio in base alle lettere del nome italiano:

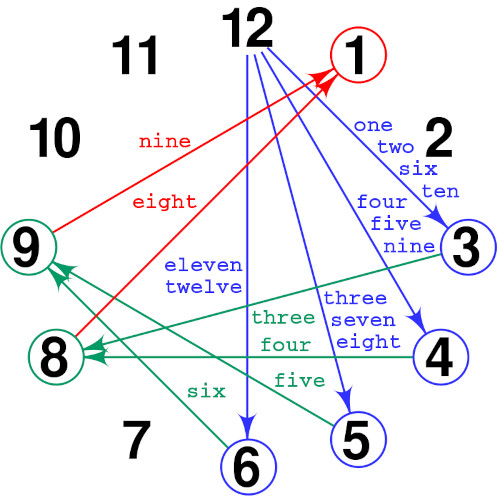
1, 2, 3, 6 -> 3
8, 9 -> 4
7, 10 -> 5
5, 11, 12 -> 6
4 -> 7

A questo punto portando avanti la serie, scopriamo che esistono due gruppi di catene distinti, quelle generate da 1, 2, 3, 4, 6, 8, 9, 10 che convergono a 5 dopo 7 passi, mentre le restanti catene di 5, 7, 11, 12 convergono a 11 dopo 9 passi. C'è da notare, a questo punto, che le prime 8 catene convergono invece a 11 dopo 8 passi, quindi potremmo anche concludere che le catene convergono allo stesso numero dell'orologio, ma non contemporaneamente, quindi non potremmo considerarlo come il punto di convergenza cercato in senso stretto. La cosa, però, non ha grande importanza, perché comunque dopo 9 passi le prime 8 catene convergono a 5 e le ultime 4 a 11. E possiamo quindi essere comunque soddisfatti, visto che il risultato di Kruskal di cui abbiamo discusso nel Rompicapo corrispondente non implica l'esistenza di un unico punto di convergenza delle catene.