I rompicapi di Alice: Tetramini

Il 6 giugno del 1984 veniva rilasciato per la prima volta il gioco del Tetris. Era stato ideato dal programmatore russo Aleksèj Leonìdovič Pažìtnov mentre lavorava presso l'Accademia delle Scienze dell'URSS di Mosca. Il gioco consiste nell'impilare uno sull'altro 7 figure piane irregolari costituite da 4 quadrati. Non appena il giocatore completa una riga, questa sparisce, facendo abbassare di uno, o più, il livello massimo raggiunto. Il gioco finisce quando si trova sullo schermo almeno uno dei quadrati di base raggiunge il limite superiore dello schermo di gioco. Gli elementi grafici con cui il giocatore si diletta sono i tetramini, cui lo stesso Pažìtnov si è ispirato per l'ideazione del Tetris.

Come detto prima, il tetramino è una figura geometrica costituita da quattro quadrati, connessi uno all'altro tramite un lato, ovvero ciascun quadrato condivide almeno un lato con i vicini.
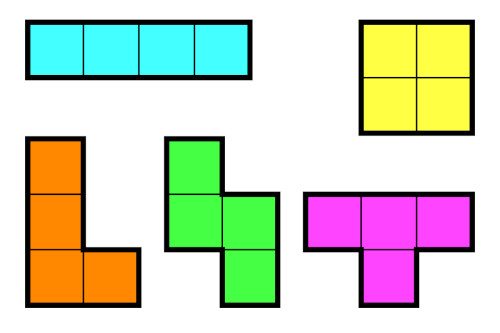
I tetramini di base, detti "liberi", sono 5: una linea orizzontale, un quadrato, una figura detta "t", una figura detta "l" o "j" (dipende da come la guardi) e l'ultima della "s" o "z" (anche in questo caso dipende da come la guardi). E' evidente, a questo punto, che se il modo in cui si guarda la figura diventa importante, allora i tetramini da 5 passano a 7. In questo caso per ottenere i due aggiuntivi basta applicare a tutti l'operazione di riflessione rispetto all'asse centrale. Dei 5 "liberi" 3 restano invariati e mentre dagli altri 2 ne vengono generati altri 2, ottenendo alla fine i tetramini usati nel Tetris.
Possiamo, però, ulteriormente aumentare il numero dei tetramini aumentando il numero di operazioni di simmetria da applicare. Ad esempio se prendiamo la "j" ruotandola di 90° otteniamo 4 tetramini distinti; quindi riflettendo ciascuno rispetto a una linea posta sotto al tetramino ne otteniamo altri 4 per un totale di 8. Applicando la tecnica agli altri tetramini "s", "t", linea e cerchio alla fine otteniamo un totale di ben 19 tetramini, detti "fissi"!
Visto che il Tetris implica l'incastro dei tetramini, allora ci possiamo chiedere se possiamo utilizzarli per ricoprire completamente un rettangolo. Si scopre che non è possibile, utilizzando un unico insieme di tetramini "liberi", nessun rettangolo. E la cosa vale anche per i tetramini del Tetris, ovvero la disposizione migliore conterrà almeno un buco come ad esempio nel rettangolo 7 × 3 con i tetramini "liberi", o ben due buchi con i tetramini del Tetris nel rettangolo 6 × 5. Con i tetramini "fissi", invece, si ottiene un buco nel caso del rettangolo 11 × 7.
Se invece prendiamo due insiemi di tetramini, è possibile trovare rettangoli che vengono completamente coperti da una qualche disposizione di tetramini, come per esempio i rettangoli 5 × 8 e 4 × 10 con i tetramini "liberi" (potete provare voi a riempirli su transum.org) e i rettangoli 8 × 7 e 14 × 4 con i tetramini del Tetris.
Per concludere torniamo al Tetris. Ciò che piacerebbe a qualunque giocatore è riuscire a realizzare la partita perfetta, che per questo gioco implica giocare all'infinito, senza mai perdere. Peccato che una ventina di anni fa è stato dimostrato (dettagli tecnici arXiv) che un'eventualità del genere è impossibile, e non per raggiunti limiti di età del giocatore, ma proprio perché la sconfitta è certa. Al massimo si può allungare la partita il più possibile, che poi alla fine è quello che interessa al videogiocatore quando inizia (quando perde la pensa in maniera differente...). Il motivo sta nel fatto che prima o poi, in una sequenza infinita di tetramini, giungerà sicuramente una combinazione di essi che renderà vano qualsiasi tentativo di... salvare l'esito finale della partita.
Ultima curiosità: il 22 marzo del 1996 Nintendo rilascia il Tetris 3D. E, come ovvio, oltre alla loro versione tridimensionale, ci sono anche i tetramini tridimensionali, ovvero i tetracubi, ovvero solidi costituiti da quattro cubi che condividono almeno una faccia. In questo caso abbiamo 10 tetracubi rispetto ai 7 tetracubi del Tetris.