Ho trovato piuttosto curiosa la richiesta di risoluzione inversa del fattoriale, in particolare quel "matematicamente", che ovviamente presuppone di suggerire metodi non algoritmici (nell'idea moderna di algoritmo, ovvero una serie di istruzioni automatiche da far eseguiore a un calcolatore). Non mi metterò a rispondere alla domanda, o almeno non fornirò un metodo in grado di fornire sempre la risposta (nelle risposte troverete che il metodo da seguire è quello dei criteri di divisibilità), ma colgo l'occasione per parlare brevemente di fattoriale.
Il fattoriale è l'operazione matematica così definita:
\[n! = n \cdot (n-1) \times (n-2) \times \dots \times 2 \times 1 = \prod_{i=1}^n i\]
ovvero il fattoriale, per esempio, di 5 è il prodotto di tutti i numeri interi positivi che precedono il 5, quest'ultimo incluso. Il risultato in questo caso specifico porta a 120.
Per come è definito il fattoriale, in particolare per come è scritto nell'estrema destra della formula, calcolare \(0!\) non avrebbe alcun senso, però possono capitare occasioni in cui ci si troverebbe di fronte a questa situazione, per cui ha senso definire il suo valore. Per fare ciò basta seguire questo ordine di uguaglianze:
\[1 = \prod_{i=1}^1 i = 1! = 1 \times (1-1)! = 1 \times 0!\]
da cui
\[0! = 1\]
Effettivamente sembra che sia nella matematica indiana, sia in quella ebraica e islamica venisse utilizzato per il calcolo delle permutazioni, per esempio per calcolare quante parole possono essere formate, indipendentemente dal loro senso compiuto, a partire da un dato numero \(n\) di lettere (ovviamente non è spiegato in questi termini!).
Se, però, prendiamo il fattoriale come una funzione a numeri interi, potremmo chiederci se è possibile trovare una funzione analitica che la approssima. E qui arriva la così detta approssimazione di Stirling:
\[f(n) = \sqrt{2 \pi n} \left ( \frac{n}{e} \right )^n\]
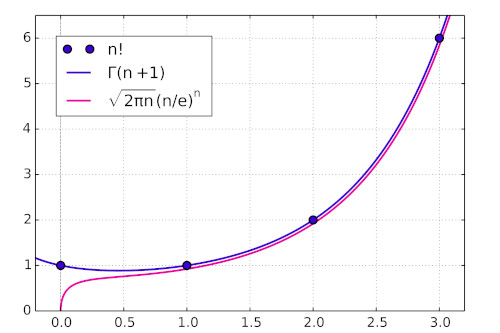
Questa approssimazione, scoperta per la prima volta dal francese Abraham de Moivre, che però non era stato in grado di calcolare la costante, venne proposta nella sua forma attuale dallo scozzese James Stirling. Ed effettivamente è un'approssimazione molto buona del fattoriale:
Nel grafico siu può vedere, anche, un confronto con una funzione analitica che, in realtà, viene considerata una espressione esatta del fattoriale, la così detta Gamma di Eulero, che a sua volta è collegata al problema della così detta ipotesi di Riemann. Questa, però, è un'altra storia!

Nessun commento:
Posta un commento