Se infatti prendiamo l'area del cerchio, ovvero \(\pi r^2\) e la deriviamo rispetto a \(r\) otteniamo \(2\pi r\), che è la misura della circonerenza, ovvero il perimetro del cerchio. Stessa cosa succede per il volume della sfera, \(4/3 \pi r^3\), la cui derivata rispetto al raggio è \(4 \pi r^2\) ovvero l'area della superficie della sfera. Questo fatto non è casuale e almeno un paio di utenti di Quora hanno spiegato la cosa con dettagli tecnici che, per quanto corretti, forse sono eccessivi. Non a caso qualcuno chiedeva nei commenti a queste risposte tecniche, una spiegazione che fosse comprensibile con la matematica delle scuole superiori.
In effetti ci sono, tra le risposte, molte che spiegano questo fatto proprio con la matematica delle superiori, in particolare quella degli ultimi anni, ovvero derivate e integrali. In particolare partiamo dal significato geometrico di integrale.
L'idea dietro l'operazione di integrale nasce da lontano, in particolare dal metodo di esaustione utilizzata da Archimede per il calcolo dell'area del cerchio, e dunque del valore del \(\pi\), e per il calcolo del volume dell'unghia.
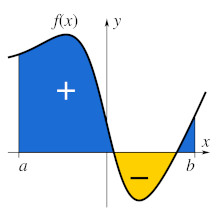
L'idea è quella di suddividere la superficie compresa tra una curva e l'asse orizzontale in tanti parallelogrammi e misurarne l'area: la somma di queste aree fornirà una stima dell'area totale. Man mano che questa suddivisione si fa più fitta, il valore di questa somma sarà sempre più vicino all'area corretta fino al limite in cui abbiamo suddiviso l'area in un numero infinito di parallelogrammi. Quando si passa all'operazione di limite, secondo la matematica moderna, la somma di infiniti parallelogrammi diventa l'usuale integrale definito. Il simbolo di integrale attualmente in uso, una "S" allungata, venne introdotto da Gottfried Leibniz, che in maniera indipendente da Isaac Newton e Johann Bernoulli, dimostrò il così detto teorema fondamentale del calcolo integrale, in cui il problema del calcolo dell'area viene ricondotto alla ricerca di una funzione primitiva di quella presa \(f\) in considerazione, ovvero di una funzione \(F\) la cui derivata \(F'\) coincide con \(f\) a meno di una costante.
Questo, quindi, stabilisce un legame tra la funzione \(f\) che rappresenta il contorno della curva e la funzione \(F\), che quindi secondo la lettura geometrica dell'integrale è la funzione che rappresenta l'area della curva. Lo stesso ragionamento vale, quindi, anche per la funzione a due variabili che rappresenta la superficie di una sfera e la sua primitiva che rappresenta il volume della sfera. E così via andando a dimensioni superiori (che ovviamente la nostra mente tridimensionale fa fatica a immaginare!).

Nessun commento:
Posta un commento