Le grandi domande della vita: Di perimetri, aree e volumi

E' raro, ma a volte succede, che mi imbatto nelle domande per questa serie nella sezione italiana di Quora. Tutto parte da una interessante osservazione sul legame tra area e perimetro di un cerchio e tra volume e area della superficie di una sfera.
Se infatti prendiamo l'area del cerchio, ovvero \(\pi r^2\) e la deriviamo rispetto a \(r\) otteniamo \(2\pi r\), che è la misura della circonerenza, ovvero il perimetro del cerchio. Stessa cosa succede per il volume della sfera, \(4/3 \pi r^3\), la cui derivata rispetto al raggio è \(4 \pi r^2\) ovvero l'area della superficie della sfera. Questo fatto non è casuale e almeno un paio di utenti di Quora hanno spiegato la cosa con dettagli tecnici che, per quanto corretti, forse sono eccessivi. Non a caso qualcuno chiedeva nei commenti a queste risposte tecniche, una spiegazione che fosse comprensibile con la matematica delle scuole superiori.
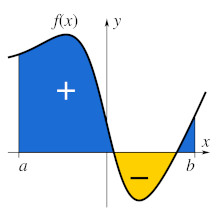
In effetti ci sono, tra le risposte, molte che spiegano questo fatto proprio con la matematica delle superiori, in particolare quella degli ultimi anni, ovvero derivate e integrali. In particolare partiamo dal significato geometrico di integrale.
L'idea dietro l'operazione di integrale nasce da lontano, in particolare dal metodo di esaustione utilizzata da Archimede per il calcolo dell'area del cerchio, e dunque del valore del \(\pi\), e per il calcolo del volume dell'unghia.

I rompicapi di Alice: Una questione di segni

Prendiamo una retta e fissiamo su di essa un punto che chiamiamo origine: sarà il nostro 0. Segnamo a destra di questo punto (o a sinistra: il concetto dietro non cambia) un secondo punto. In questo modo abbiamo compiuto due operazioni: definito la nostra unità, l'1, e dato un verso alla retta. E proprio grazie a questa unità possiamo definire tutti gli altri numeri presenti sulla retta ordinata degli interi, prima spostandoci di un passo alla volta verso destra (o sinistra) definnendo così i numeri positivi, quindi spostandoci di un passo alla vola verso sinistra (o destra) definendo così i numeri negativi. Il tutto, ovviamente, a partire dallo 0.
Questo, ovviamente, è solo un modo geometrico per vedere i numeri negativi, che i greci avevano già incontrato ritenendoli semplicemente assurdi. Si narra, infatti, che Diofanto incontrò per la prima volta i numeri negativi quando risolse un'equazione di primo grado che in termini moderni può essere scritta come \(4x + 20 = 4\) che ha come soluzione \(x = -4\). In questo caso il matematico greco ritenne che proprio tutta l'equazione era da considerarsi assurda. Questa posizione discende abbastanza naturalmente dal fatto che i matematici greci erano anche dei geometri, e una misura negativa non aveva alcun senso.
I numeri negativi, però, non erano così spaventevoli per i matematici di altre parti del mondo, come per esempio i matematici cinesi, quelli indiami o quelli arabi, dai quali Fibonacci portò in Europa anche il concetto dello zero.