Questo nuovo rompicapo, introdotto da Miyamoto, un insegnante, per rendere più divertenti e quindi semplici da imparare le operazioni, prende le mosse dal quadrato latino. Prendiamo un quadrato \(n \times n\). La regola è riempire ciascuna casella in modo tale che in ciascuna riga e ciascuna colonna siano presenti solo i numeri da 1 a \(n\) senza ripetizioni: un'estensione del Sudoku, insomma! Miyamoto, però, aggiunse una regola aggiuntiva: la "scacchiera", infatti, viene suddivisa in un certo numero di "gabbie". I numeri da scegliere per ciascuna "gabbia", se sommati tra loro, devono avere come risultato il numero in picco posto in cima alla "gabbia". Prendiamo come esempio il seguente schema 4x4, quindi da riempire con i numeri da 1 a 4:
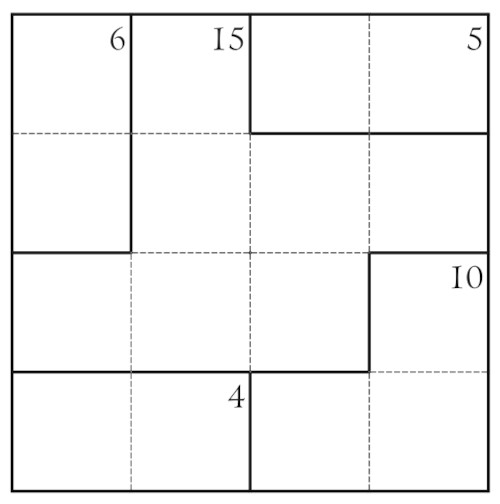
Qui la gabbia con somma 4 può essere riempita solo da 1 e 3, quindi nelle due celle sulla stessa riga andranno 4 e 2. Queste due celle appartengono a una gabbia di 3 celle che in totale ha 10, questo vuol dire che nella terza cella ci andrà 4, il che implica che in posizione (4,4) ci andrà il 2 e quindi nella terza e ultima cella, la (4,3), dovremo mettere 4, e questo per la regoma che non devono esserci ripetizioni nemmeno lungo le colonne.
A questo punto siamo certo che la gabbia 5, proprio a causa della regola di cui sopra, deve contenere 2 e 3, e quindi in posizione (1,1) avremo il 4 e in posizione (2,1) avremo 2.
Non solo! Potremo anche completare la prima riga con tutti i numeri, rispettivamente 1, 2 e 3, e questo perché sappiamo che in posizione (4,4) ci deve essere un 2.
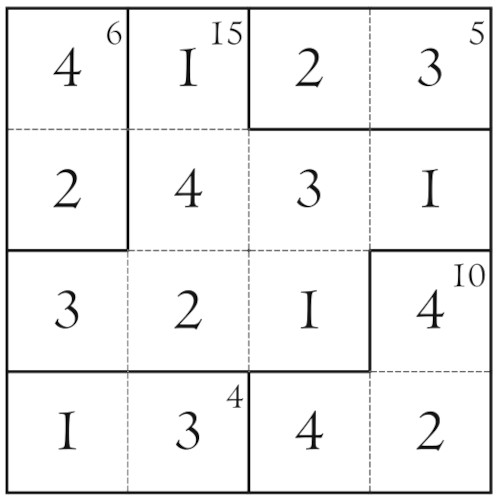
Non proseguo oltre con i ragionamenti e vi presento la soluzione di questo Calcudoku (e lo faccio senza problemi perché non è questo il rompicapo che voglio proporvi da risolvere):
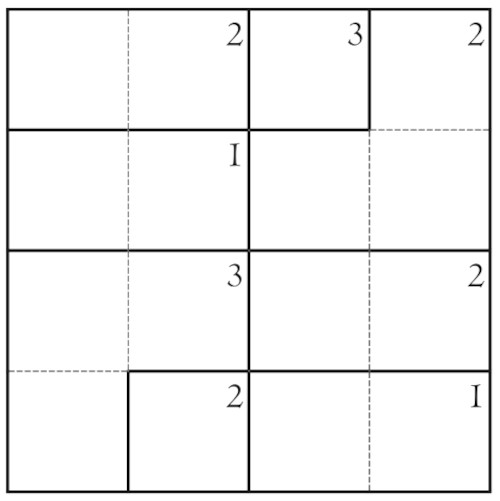

Nessun commento:
Posta un commento