La fisica dello sci

Credo che, dal punto di vista della fisica, non ci sia uno sport più completo dello sci. A un primo livello basilare, lo sci si riduce a una questione di attrito tra l'attrezzo e la neve. La situazione ideale, ovviamente, è la completa assenza di attrito, cosa che non è vera nemmeno con la neve: non a caso ogni volta che passiamo sulla neve, questa si scioglie e questo perché parte dell'energia che usiamo per camminare viene trasferita alla neve proprio dall'attrito.
Ovviamente di discipline sciistiche ce ne sono diverse: discesa, sci di fondo, salto, sci acrobatico. Mi manterrò sulla discesa.
In questo caso, quindi, nella situazione ideale ci si aspetta che tutta l'energia potenziale dello sciatore (sì, iniziamo a piazzare lo sportivo sugli sci) si trasformi in energia cinetica. Come detto ciò non avviene nemmeno con la neve, e infatti sono state sviluppate forme più efficienti per gli sci, anche dal punto di vista aereodinamico (a questo ci arriveremo tra poco), ma soprattutto sono state ideate diversi tipi di scioline. Questo perché non tutti i tipi di scioline vanno bene per tutti i tipi di neve.
Le proprietà fisiche della neve, infatti, si modificano leggermente in funzione della temperatura dell'aria o dell'umidità. E per vari intervalli di questi parametri sono stati sviluppati tipi di sciolina che riducono il più possibile l'attrito tra l'attrezzo e la superficie ghiacciata. Si può, poi, fornire un esempio abbastanza semplice da capire sulle differenze tra i tipi di neve: possiamo ad esempio essere su una distesa di neve in una giornata limpida con il Sole in cielo e la temperatura al di sotto dewllo 0, oppure in una giornata nuvolosa, con una leggera pioggia che cade sul manto nevoso. Queste due condizioni differenti creano due tipi diversi di neve. E quindi due scioline diverse.
Le cose iniziano a diventare interessanti quando iniziamo a considerare lo sciatore che, sugli sci, si sta lanciando nella discesa. Anche il nostro sportivo oppone una certa resistenza all'avanzamento. La forza di attrito che lo rallenta è data dall'equazione \[F_D = \frac{1}{2} C_D \rho A v^2\] dove \(C_D\) è il coefficiente di attrito (consideriamo quello dinamico), \(\rho\) la densità dell'aria, \(A\) la superficie dello sciatore perpendicolare alla direzione del moto, \(v\) la sua velocità.
E' quindi evidente che lo sciatore, per ridurre il più possibile la forza d'attrito, deve raccogliersi il più possibile nella così detta "posizione a uovo", tipica peraltro dei discesisti. In questo caso anche la massa dello sciatore gioca un ruolo importante nell'aumentare la velocità della discesa.
Oltre ai discesisti, però, ci sono in giro anche gli slalomisti, che potremmo quasi considerare i fiorettisti della neve, visto che devono ottimizzare non solo la velocità, ma anche la precisione: in fondo devono curvare nel loro percorso e non è per nulla semplice modificare la direzione in discesa e in una situazione con attrito minimo o nullo.

Per capire al meglio la siatuazione iniziamo a mettere in fila ciò che sappiamo. Lo sciatore sta scendendo lungo un piano inclinato, quindi con una inclinazione \(\alpha\). Gli sci, poi, non sono perpendicolari rispetto alla linea che unisce i punti che si trovano alla stessa quota (in termini tecnici i punti equipotenziali) e hanno anch'essi, rispetto a questa linea, una data inclinazione, \(\beta\). Infine lo slalomista approccia l'operazione del curvare con un arco di un dato raggio \(R_T\), che ovviamente il nostro cerca di mantenere il più vicino possibile alla bandierina.
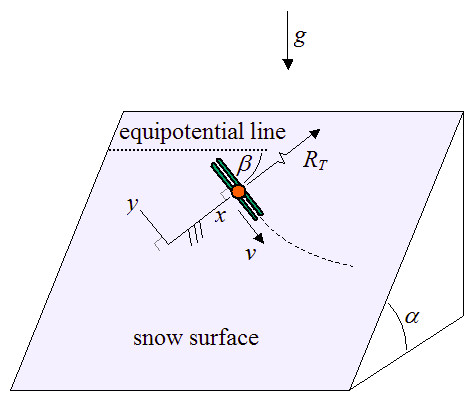
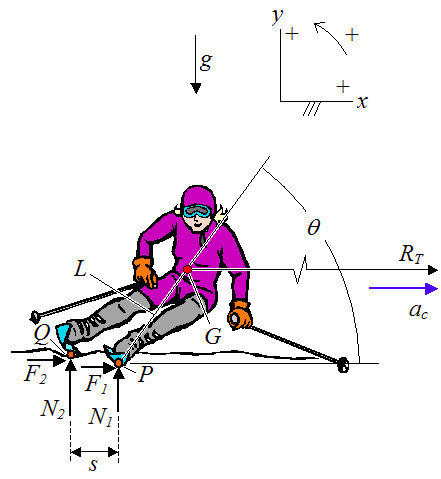
Andiamo allo sciatore. Innanzitutto defininiamo come sci più interno quello più vicino al centro della curva, quindi lo sci sinistro in caso di curva a sinistra, e quello destro nel caso opposto. Questo ci permette di definire l'angolo di inclinazione del corpo dello sciatore, \(\vartheta\), come l'angolo tra la superficie della neve e la linea che unisce il punto \(P\) più interno dello sci più interno con il centro di massa \(G\) dello sciatore. Inoltre lo slalomista sta affrontando una curva, quindi entra in gioco anche il moto circolare uniforme. In particolare l'accellerazione centripeta \(a_c\), quella che tende a portare lo sciatore verso il centro della curva.
Ultima, ma non per questo meno importante, l'accellerazione di gravità \(g\): non dimentichiamo dove ci troviamo!

Prima di tirare fuori le equazioni che descrivono l'atto di curvare del nostro slalomista, definiamo due forze in particolare, le forze di contatto (o le reazioni) tra la neve e lo sciatore. Queste, una per ciascuno sci (quindi due) le suddividiamo nelle due componenti orizzontali, \(F_{1, 2}\), e verticali, \(N_{1, 2}\). Quelle orizzontali spingono lo sciatore verso il centro della curva. Quelle verticali lo spingono verso l'alto.
A questo punto siamo pronti!
Con la prima equazione vediamo il moto lungo l'asse verticale: \[N_1 + N_2 - mg \cos \alpha = 0\] dove in \(m\) bisogna considerare non solo la massa dello sciatore, ma anche quella degli sci.
Per quel che riguarda il moto orizzontale, invece, abbiamo \[F_1 + F_2 - mg \sin \alpha \cos \beta = m a_c\] In entrambe le queazioni sono stati considerati innanzitutto il fatto che stiamo descrivendo un oggetto lungo un piano inclinato, da qui la presenza dell'angolo \(\alpha\), e quindi il fatto che gli sci sono, in qualche modo, inclinati rispetto alla linea equipotenziale, ed ecco spuntare l'angolo \(\beta\). Infine l'accelerazione centripeta è data dall'equazione \[a_c = \frac{v^2}{R_T}\] La cosa, però, non è finita qui, perché c'è una terza equazione da considerare. Dobbiamo considerare anche il fatto che lo slalomista mentre affronta la curva, inclina il corpo all'interno e verso il basso, quindi ecco la necessità di descrivere anche l'inerzia di questa azione: \[(F_1 + F_2) \sin \vartheta \cdot L - N_1 \cos \vartheta \cdot L - N_2 \left ( L \cos \vartheta + s \right ) = 0\] dove \(L\) è la distanza tra \(P\) e \(G\), \(s\) è la distanza tra i due sci, mentre l'uguaglianza con 0 esprime una sitazione di equilibrio, come nell'equazione verticale.
In particolare quest'ultima equazione ci fa capire che l'angolo con cui lo sciatore si piega non può essere eccessivamente basso, pena la perdita dell'equilibrio e quindi la rovinosa caduta sulla neve. Questo lo si comprende anche senza aver mai provato in prima persona o visto come funziona la cosa semplicemente guardando la funzione trigonometrica al cui interno si trova \(\vartheta\): un coseno. Il coseno ha il suo valore massimo quando l'angolo è nullo (o quando è 360°), ma il valore è prossimo a 1 anche per angoli che si discostano da poco da 0 (in radianti). Se trasferiamo questo alla situazione fisica, man mano che l'angolo di inclinazione dello sciatore diminuisce, la di reazione della neve aumenta, e ciò fa a sua volta diminuire l'angolo in un effetto che, se non è tenuto sotto controllo, porta all'inevitabile caduta.
Da tutto questo ho tenuto fuori ulteriori considerazioni come quella sulla forma degli sci, per non tacere delle altre discipline sciistiche in questo periodo protagoniste delle Olimpiadi Invernali. Ulteriori approfondimenti li potete trovare su The Physics Of Skiing e Understanding The Physics Of Ski Racing, da cui ho preso le immagini a corredo di questo articolo.