
E' la probabilità, bellezza!
Il paradosso, che forse dovremmo chiamare più correttamente problema del compleanno, sembra che venne portato alla luce per la prima volta nel 1927 da Harold Davenport, solo che decise di non pubblicare nulla a rigurado, perché era convinto che fosse già stato scoperto prima. E invece il primo a pubblicare un articolo su questo particolare quesito fu Richard von Mises nel 1939.Come problema potremmo enunciarlo in questo modo (riprendo il testo dal libro di Palmigiani):
Quanto è probabile che in un gruppo di 30 persone vi siano due nate lo stesso giorno?
Chiunque di noi risponderebbe qualcosa del tipo poco. Ma quanto è poco questo poco?La cosa interessante del questo è che ritorna spesso nelle conversazioni, e quando qualcuno ne racconta, in maniera più o meno approssimativa, la risposta, tutti restano un po' perplessi, anche gente che la matematica la sa, visto che così, su due piedi, la risposta non sembra per nulla sensata.
Se iniziassimo, infatti, a ragionare in modo classico, diremmo: la probabilità di essere nato in un dato giorno dell'anno e 1/365 (escludiamo, per semplicità, gli anni bisestili), che è una probabilità effettivamente piuttosto bassa, poco meno di 0.003, per cui chiunque sarebbe portato a pensare che anche la probabilità che due persone in un gruppo relativamente piccolo siano nate lo stesso giorno sia dello stesso ordine di grandezza, a voler essere fortunati.
Un ragionamento più raffinato è quello di partire dal caso gruppo costituito da 366 persone: in questo caso, sempre escludendo l'anno bisestile, la probabilità è 1. E quindi l'idea è procedendo per sottrazione. Essendo però un numero dell'ordine delle centinaia, ci si perde ben presto nei conti e soprattutto nel ragionamento.
Un modo più semplice e più proficui, invece, è quello di ragionare al contrario: determinare la probabilità che tutti hanno compleanni diversi. In questo caso, inserendoci all'interno del gruppo, la probabilità che la seconda persona abbia un compleanno diverso dal mio è 364/365. La probabilità che la terza persona abbia un compleanno diverso da me e dalla seconda è 363/365. Per la quarta vale 363/365 e così via. Per cui la probabilità che tutti i componenti del gruppo abbiano un compleanno diverso è il prodotto di ciascuna di queste probabilità: \[P = \frac{364}{365} \cdot \frac{363}{365} \cdot \frac{362}{365} \cdots \frac{365-N+1}{365}\] Più in generale, utilizzando il fattoriale (\(n! = n \cdot (n-1) \cdot (n-2) \cdots 3 \cdot 2 \cdot 1\)), questa probabilità in formule può essere così espressa: \[P = \frac{365!}{(365-N)!} \cdot \frac{1}{365^N}\] dove \(N\) è la cardinalità del gruppo di persone prese in considerazione. Quindi la probabilità che almeno due persone festeggino il compleanno lo stesso giorno è data da \(1-P\).
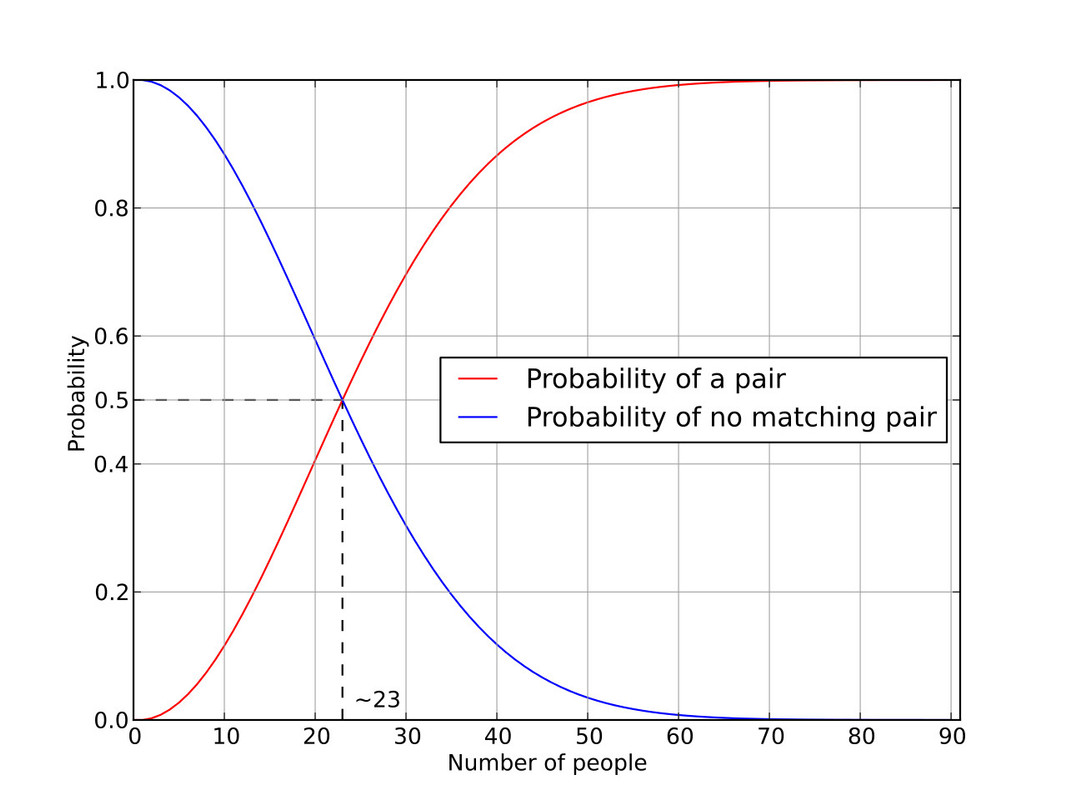
Le formule, messe così, ci dicono poco fino a che non ci mettiamo dentro i numeri, ma se poi le grafichiamo ci forniscono delle informazioni ancora più preziose. Per cui, se grafichiamo le due probabilità in un unico grafico, in blu \(P\) e in rosso \(1-P\), scopriamo che con 23 persone la probabilità è all'incirca 50% e con 30 siamo intorno al 70% (71% se ho fatto bene i conti con la calcolatrice).

Nessun commento:
Posta un commento