
Il punto centrale è che la distinzione vera tra fisica classica e meccanica quantistica non è fornita dal macro o dal micro, ma dal genere di termodinamica che viene utilizzata per studiare un dato sistema. L'esempio più ovvio che abbiamo sotto gli occhi ogni giorno (anche se non dobbiamo dimenticarci di non osservarlo mai direttamente) è il Sole. La stella che illumina il nostro pianeta, infatti, è una vera e propria fornace nucleare e quindi la sua evoluzione e i moti delle particelle (fotoni, elettroni, nucleoni) vengono descritti usando le equazioni della meccanica quantistica, eppure il Sole non può certo essere definito un sistema microscopico. D'altra parte per descrivere il moto del Sole all'interno della galassia utilizziamo le leggi della gravitazione scoperte da Isaac Newton in prima approssimazione o la relatività generale di Albert Einstein per fornire una descrizione più precisa. Ovvero, in funzione di cosa ci interessa capire del Sole, lo descriviamo ora con le leggi della meccanica quantistica, ora con quelle della fisica classica. Se hai presente i supereroi, potremmo dire che accade la stessa cosa anche con la Torcia Umana dei Fantastici 4!
Usiamo questo supereroe per chiarire meglio le differenze tra fisica classica e meccanica quantistica: fino a che Johnny Storm resta un essere umano normale, possiamo utilizzare le equazioni di un corpo rigido per descriverlo grossolanamente. Nel momento in cui si infiamma, diventando la Torcia Umana, risultano necessarie le equazioni della meccanica quantistica: la principale differenza tra i due approcci è, però, non tanto il macro e il micro, ma il numero di elementi che trattano. Le equazioni della fisica classica trattano un numero di oggetti relativamente limitato. Quelle della meccanica quantistica sono in grado di trattare sistemi costituiti da un numero elevato di particelle. Per capire meglio, se prendiamo il problema dei tre corpi (giusto per restare nel campo dell'astronomia), questo, pur basandosi su equazioni classiche relativamente semplici, conduce a soluzioni caotiche o statistiche, proprio come le equazioni della meccanica quantistica.
Per quel che riguarda lo zoom, ti lascio con questa immagine data dal fisico teorico John Wheeler:
Non conosco un'immagine migliore di quella di guardare l’oceano dall’alto di un aereoplano: sembra essere una superficie perfettamente liscia. Man mano che ti avvicini, vedi le onde, e mentre i avvicini ancora vedi le onde che si infrangono e vedi la schiuma. Penso che debba essere lo stesso nella geometria dello spazio, per tutta la nostra esperienza quotidiana, la geometria dello spazio è liscia e piatta. Ma mentre lo esaminiamo più da vicino, deve mostrare oscillazioni. E ancora più da vicino, deve mostrare la schiuma, una struttura simile alla schiuma. E questo significa che sotto a distanze piccolissime questa idea del prima e del dopo perde davvero di significato.(1)
Due o tre cose sullo spin
Il testo che segue è una risposta a una domanda piuttosto complessa sullo spin. Per i curiosi rimando all'articolo linkato in precedenza per i dettagli sulla domanda stessa. Qui cerco di integrare il tutto in un'unica sezione il più armonizzata possibile tra le varie parti.Partiamo con la definizione di spin: essa è indipendente dal fatto che l'elettrone, o qualsiasi altra particella, possegga delle dimensioni o meno.
Per capire cosa sia lo spin, utilizzerò un concetto tecnico che spero non sia eccessivamente complesso: la simmetria. Le simmetrie sono operazioni matematiche che trasformano, ad esempio, le figure geometriche di un dato spazio in altre figure geometriche. Un esempio semplice di simmetria ce lo abbiamo ogni mattina quando ci guardiamo allo specchio: i lati sinistro e destro della nostra faccia sono, all'incirca, identici e dunque simmetrici rispetto al naso, che è il nostro asse di simmetria.
In fisica lo studio delle simmetrie è particolarmente importante, perché dal punto di vista matematico studiare le proprietà di simmetria di un sistema (ovvero ciò che non viene e ciò che viene modificato dalla trasformazione di simmetria) risulta più semplice rispetto ai calcoli veri e propri. Questo perché molte proprietà fisiche sono associate a particolari trasformazioni di simmetria, e lo spin è una di queste.
In particolare lo spin è associato alla rotazione. In termini semplici si dice che lo spin è associato al verso di rotazione della particella, che però in questa visione viene vista come una pallina o una trottola, cosa che non è esattamente corretta, sebbene non la si possa nemmeno considerare puntiforme, neanche una particella elementare come l'elettrone.
In termini un po' più corretti, invece, lo spin non è legato a una rotazione effettiva, ma al fatto che il sistema fisico che stiamo studiando fornisce una certa risposta quando si applica su di esso una rotazione.
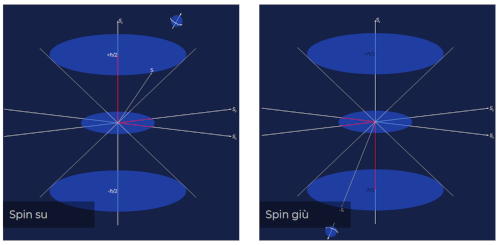
In altri termini non possiamo prevedere quale sarà il risultato della misura prima di averla compiuta. Al massimo possiamo calcolare la probabilità di ottenere un certo risultato piuttosto che un altro: è quindi in questi termini che si considera indeterminato lo spin di una particella.
Vediamo, ora, cosa accade allo spin in caso di interazione tra particelle (ricordo che quanto segue è una semplificazione, avendo escluso qualunque trattazione matematica dal post).
Fino a che una particella è isolata, il suo spin resta costante. Quando invece interagisce con un'altra particella, allora entra in gioco il principio di conservazione dello spin totale del sistema: la somma degli spin delle due o più particelle prima dell'interazione è uguale alla somma degli spin dopo l'interazione. Poiché il campo elettromagnetico è costituito a sua volta da particelle, i fotoni (quelli che trasportano la luce), allora anche nel caso del protone rallentato dal campo elettrico, ci può essere cambio di spin del protone solo se risulta modificato anche lo spin del fotone con cui interagisce il protone in moto.
L'obiettivo dell'interazione con il campo elettrico che descrivi nella tua domanda, però, ha come obiettivo quello di modificare la quantità di moto del protone, non il suo spin. E questo vuol dire che, in linea di principio, non tutte le volte che avverrà l'interazione con il fotone ci sarà anche un cambio dello spin.
- I don't know any better image for it than the look of the ocean as one comes down from a plane high above the ocean, that seems to be a perfectly smooth surface. You come down closer, you see the waves, and as you get still closer you see the waves breaking and you see foam. I think it must be the same in the geometry of space, for all our everyday experience, the geometry of space is smooth and flat. But as we examine it more closely, it must show oscillations. And still more closely, it must show foam, a foam-like structure. And that means that down at the very smallest distances, this idea of before and after really lose their meaning. ↩︎

Nessun commento:
Posta un commento