Se prendiamo due resistenze in un circutio, possiamo calcolare il valore della resistenza equivalente in funzione del fatto se le due resistenze sono in serie
\[R_{tot} = R_1 + R_2\]
o in parallelo
\[R_{tot} = \frac{R_1 R_2}{R_1 + R_2}\]
Prendiamo ora un circuito costituito da un numero infinito di resistenze sistemate come segue:
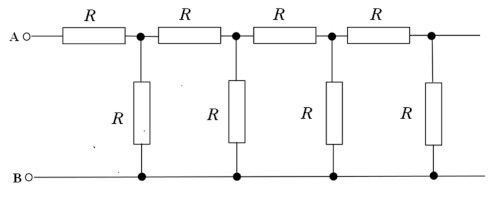
Proviamo a fare un paio di calcoli con le resistenze che si vedono nell'immagine. Ad esempio concentriamoci sulla prima maglia da destra. In quel caso la resistenza equivalente è pari a
\[\frac{2}{3} R\]
Aggiungendo la resistenza subito in serie a questa otteniamo
\[\frac{5}{3} R = R_1\]
Calcoliamo ora la resistenza equivalente delle prime due maglie da destra:
\[\frac{5}{8} R\]
che aggiungendo la resistenza subito in serie ci fornisce un valore di
\[\frac{13}{8} R = R_2\]
A questo punto concludiamo il conto per tutte le maglie esclusa la resistenza iniziale
\[\frac{13}{21} R\]
e aggiungendo la prima resistenza otteniamo
\[\frac{34}{21} R = R_3\]
I coefficienti davanti alle resistenze dovrebbero ricordarvi qualcosa, ma se non lo fanno proviamo con un altro approccio, più teorico.
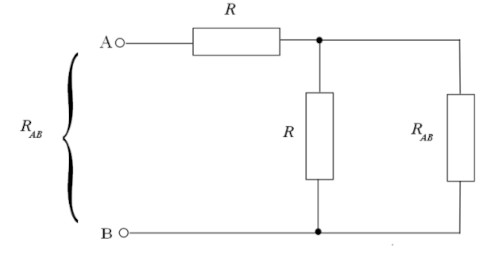
Innanzitutto riduciamo il circuito in questo modo
La resistenza equivalente totale sarà data da
\[R_{AB} = R + R_0\]
dove \(R_0\) è data dalla resistenza in parallelo tra \(R\) e \(R_{AB}\) della prima maglia:
\[R_0 = \frac{R R_{AB}}{R+R_{AB}}\]
Sostituendo la seconda equazione nella prima si ottiene un'equazione di secondo grado in \(R_{AB}\) che ha come risultato positivo
\[R_{AB} = \frac{1+\sqrt{5}}{2} R\]
che altro non è se non il numero aureo!
D'altra parte i coefficienti della resistenza equivalente che ho chiamato \(R_1\), \(R_2\), \(R_3\) di una particolare frazione continua che permette di calcolare il rapporto aureo:
\[\varphi = 1 + \frac{1}{1+\frac{1}{1+\frac{1}{\cdots}}}\]
Atkin, K. (2021). Infinity: some close encounters in physics teaching. Physics Education, 57(2), 025015. doi:
10.1088/1361-6552/ac3932


Nessun commento:
Posta un commento