Un circuito d'oro

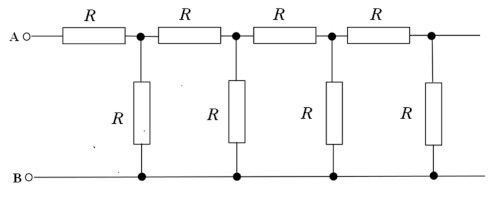
Se prendiamo due resistenze in un circutio, possiamo calcolare il valore della resistenza equivalente in funzione del fatto se le due resistenze sono in serie \[R_{tot} = R_1 + R_2\] o in parallelo \[R_{tot} = \frac{R_1 R_2}{R_1 + R_2}\] Prendiamo ora un circuito costituito da un numero infinito di resistenze sistemate come segue:

Un'equazione divina

Anche senza lo spoiler nel titolo del video (che vi metterò qui sotto) questa equazione aveva comunque qualcosa di familiare: \[\left (x - \frac{1}{x} \right )^{1/2} + \left (1 - \frac{1}{x} \right )^{1/2} = x\] A voler essere onesti il pensiero è andato prima al numero di Nepero, $e$, ma c'era un problema di segno (ci scriverò un articoletto in futuro, così potrete capire cosa intendo), e poi all'equazione che definisce il numero aureo:

La sezione aurea

Realizzato e pubblicato ormai quasi 11 anni fa da Cristóbal Vila, Nature by Numbers mostra come la matematica sia presente in tutta la natura. E la base di tutto sembra essere un piccolo, semplice numero, $\varphi$, il numero aureo. Il suo valore è di poco superiore a 3/2 e può essere scritto in maniera molto semplice con la seguente formula \[\varphi = \frac{1+\sqrt{5}}{2}\] E' anche legato alla serie di Fibonacci, come abbiamo visto in varie occasioni, e può essere ritrovato un po' d'appertutto: è diventato, in effetti, sinonimo di perfezione, grazie alla sua presenza nel mondo dell'arte. Opere di pittori, ma anche in architettura, sia dell'antichità sia degli evoluti XX e XXI secolo si basano sul numero aureo. La sua definizione si trova negli Elementi di Euclide:

Si dice che una retta è divisa in media ed estrema ragione quando la lunghezza della linea totale sta a quella della parte maggiore come quella della parte maggiore sta a quella della minore.

La definizione geometrica qui sopra può essere facilmente visualizzata con la seguente immagine:

Le grandi domande della vita: la perfezione di Olinto

Scusandomi con i lettori per il leggero ritardo nella pubblicazione della consueta rubrica, vado immediatamente a raccontarvi di un numero che attirerebbe immediatamente l’attenzione di Paperon de Paperoni!

Il numero perfetto

Un tale pose una coppia di conigli in un luogo circondato da pareti. La coppia iniziò a riprodursi a partire dalla fine del primo mese e ogni mese generò una nuova coppia di conigli. Tutte le coppie, nate nel corso dell’anno, iniziarono a riprodursi a partire dal secondo mese dopo la nascita e anch’esse generarono una nuova coppia ogni mese.
Quante coppie di conigli nascono complessivamente in un anno?

La soluzione di questo rompicapo, proposto da Leonardo Fibonacci, è la famosa serie numerica che porta il suo nome, $1$ $1$ $2$ $3$ $5$ $8$ $13$ $21$ e così via. In generale l’$n$-simo numero della serie di Fibonacci è dato da: \[F_n = F_{n-2} + F_{n-1}\]

da Paperino nel mondo dela matematica

Nel 1611 Johannes Kepler, italianizzano come Giovanni Keplero, scoprì che il rapporto tra due numeri consecutivi di Fibonacci approssimava sempre meglio il numero aureo $\varphi$, mentre per attendere un legame formale tra la serie e $\varphi$ bisogna attendere la formula scoperta da Jacques Binet: \[F(n) = \frac{\varphi^n - (1-\varphi)^2}{\sqrt{5}}\] La scoperta del numero aureo viene tradizionalmente associata al pitagorico Ippaso di Metaponto ed è legata allo studio del pentagono regolare. In particolare il numero aureo viene definito come il rapporto tra una diagonale del pentagono e un suo lato. Il fatto che il pentagono fosse una figura geometrica dagli attributi praticamente mistici per i pitagorici⁽¹⁾, ha reso lo stesso $\varphi$ un numero di una certa importanza, tanto che gli antichi greci pensavano che le proporzioni perfette, quelle del bello, fossero legate esattamente al valore di tale numero $\varphi$.
E spero sinceramente che ciò possa rispondere alla prima curiosità sul perché il numero aureo è perfetto.

Mondo Matematico: Il teorema di Pitagora

Proseguo con le recensioni/approfondimenti della collana da edicola Mondo Matematico. Dopo il volume sui numeri primi e quello dedicato alla crittografia, è oggi il turno del Teorerma di Pitagora (vi consiglio di leggere anche il post di Mauro Merlotti dedicato al teorema di de Gua, a metà strada tra dimostrazione non standard e generalizzazione di quello di Pitagora).

La setta dei numeri

Se da un lato la cavalcata nella crittografia è da considerarsi non solo una lettura interessante, ma necessaria visti i tempi, quella dedicata al teorema di Pitagora è più divertente e coinvolge concetti matematici probabilmente più leggeri, utilizzati anche nell'ambito più familiare della matematica creativa.
L'inizio è quasi leggendario: Pitagora viene infatti considerato come il primo matematico a capo di una vera e propria setta che ha fatto dei numeri quasi un oggetto di culto. Interessanti in questo senso sono i versi aurei e le regole che sono alla base della setta pitagorica e che si dimostrano molto simili ai precetti delle moderne religioni. Persino i concetti più propriamente filosofici si dimostrano incredibilmente influenti nel pensiero occidentale, ritrovandoli successivamente in filosofi come Aristotele e Platone.
I numeri avevano, dunque, un'importanza fondamentale per i pitagorici, a partire dall'1, il generatore di tutti i numeri, senza dimenticare il 2, simbolo della diversità e dell'indefinito, e il tre, unione dell'1 e del 2, simbolo dell'armonia della perfezione. Ciò non vuol dire che era considerato un numero perfetto, visto che i numeri perfetti sono tali solo se uguali alla somma dei loro divisori, 1 incluso: e il primo di questa lista è il 6. In mezzo il 4, simbolo di giustizia, e il 5, simbolo del matrimonio e del triangolo divino, facendo parte della più piccola terna pitagorica.
E con la terna entriamo nell’argomento centrale del libro: il teorema di Pitagora. E questo è l'enunciato originale così come scritto nel libro di Claudi Alsina:

Dato un triangolo con i vertici $ABC$, l'angolo $A$ è retto (triangolo rettangolo), se e soltanto se l'area del quadrato costruito sul lato $a$, opposto a $A$, corrisponde alla somma delle aree dei quadrati costruiti sui lati $b$ e $c$.

Come potete notare l'enunciato originale è un ribaltamento dell'enunciato usuale che ci viene insegnato a scuola: ciò è possibile grazie a quel "se e soltanto se" che permette di ribaltare qualunque teorema (dimostrato vero) in cui è presente.

La matematica del Nobel per la Chimica 2011

Il Nobel per la Chimica 2011 è stato assegnato a Daniel Shechtman

per la scoperta dei quasicristalli

L'articolo della scoperta, scritto con Blech, Gratias e Cahn, inizia con le seguenti parole:

Qui riportiamo l'esistenza di un solido metallico che diffrange gli elettroni come un cristallo singolo ma a un gruppo di simmetria puntuale $m \bar{35}$ (icosaedro) che è inconsistente con le traslazioni del reticolo.⁽²⁾

Le traslazioni reticolari sono, in effetti, degli strumenti molto importanti per la classificazione dei cristalli, come si capisce dalla definizione del 1992 della International Union of Crystallography:

Un cristallo è una sostanza nella quale gli atomi costituenti, le molecole, o gli ioni sono impacchettati in una struttura tridimensionale ordinata che si ripete [periodica].

La scoperta di Shechtman e colleghi era dunque molto importante: introducono, infatti, una nuova classe di cristalli, detti quasicristalli da Levine e Steinhardt solo poche settimane più tardi⁽³⁾, e un nuovo modo di vedere i cristalli stessi.
In particolare Shechtman, studiando una struttura di alluminio con il 10-14% di Manganese, insieme con i colleghi osservò che

Le simmetrie dei cristalli dettano che diversi icosaedri in una cella unitaria hanno differenti orientazioni e consentono loro di essere distorti (...)⁽²⁾

E quando osservarono il cristallo utilizzando le traslazioni reticolari:

i cristalli non possono e non esibiscono il gruppo di simmetria puntuale dell'icosaedro.⁽²⁾

Osservarono anche che la formazione della fase icosaedrica è una transizione di fase del primo ordine, poiché le due fasi (l'altra è quella delle traslazioni) coesistono per un po' durante la traslazione⁽²⁾.