I rompicapi di Alice: Di arance e salsicciotti

Era il 1611 quando Johannes Kepler si chiese quale era il modo migliore per ringraziare a costo zero (o il più basso pèossibile) il suo munifico mecenate, Johannes Matthaus Wacker von Wackenfels. Decise di scrivere un libro e dedicarglielo: Il fiocco di neve esagonale.
Kepler partiva dall'osservazione che i fiocchi di neve formavano cristalli di simmetria esagonale⁽¹⁾. La domanda aleggia già nell'aria: perché questa simmetria?
La risposta dell'astronomo e matematico era molto semplice: la simmetria esagonale è il modo più efficiente di accostare cerchi in un piano⁽¹⁾.
Ovviamente Kepler non si limitò solo ai cerchi nel piano, ma si chiese se anche con le sfere esisteva una qualche regola analoga. Di fatto per impilare oggetti di forma sferica, come le palle di un cannone o le arance, si possono in principio utilizzare tre impacchettamenti regolari: esagonale, cubico e cubico a facce centrate.
Il primo lo si ottiene impilando uno sull'altro strati di sfere a loro volta impacchettate con simmetria esagonale. In questo caso i centri delle sfere si ritrovano esattamente uno sull'altro. L'impacchettamento cubico è analogo a quello esagonale, con la differenza che ogni strato è impacchettato con la simmetria di un quadrato. E i centri sono sempre allineati uno sull'altro.
L'impacchettamento cubico a facce centrate è, invece, quello che applicano normalmente i fruttivendoli quando impilano le arance: ogni strato ha simmetria esagonale, ma lo strato superiore è incastrato nello strato inferiore facendo combaciare i centri delle sfere superiori con i vuoti dello strato inferiore⁽¹⁾.
Anche in questo caso Kepler arriva alla conclusione che l'impacchettamento cubico e facce centrate è il più efficiente possibile. E entrambe le affermazioni di Kepler vennero dimostrate solo nel XX secolo.

Le grandi domande della vita: la perfezione di Olinto

Scusandomi con i lettori per il leggero ritardo nella pubblicazione della consueta rubrica, vado immediatamente a raccontarvi di un numero che attirerebbe immediatamente l’attenzione di Paperon de Paperoni!

Il numero perfetto

Un tale pose una coppia di conigli in un luogo circondato da pareti. La coppia iniziò a riprodursi a partire dalla fine del primo mese e ogni mese generò una nuova coppia di conigli. Tutte le coppie, nate nel corso dell’anno, iniziarono a riprodursi a partire dal secondo mese dopo la nascita e anch’esse generarono una nuova coppia ogni mese.
Quante coppie di conigli nascono complessivamente in un anno?

La soluzione di questo rompicapo, proposto da Leonardo Fibonacci, è la famosa serie numerica che porta il suo nome, $1$ $1$ $2$ $3$ $5$ $8$ $13$ $21$ e così via. In generale l’$n$-simo numero della serie di Fibonacci è dato da: \[F_n = F_{n-2} + F_{n-1}\]

da Paperino nel mondo dela matematica

Nel 1611 Johannes Kepler, italianizzano come Giovanni Keplero, scoprì che il rapporto tra due numeri consecutivi di Fibonacci approssimava sempre meglio il numero aureo $\varphi$, mentre per attendere un legame formale tra la serie e $\varphi$ bisogna attendere la formula scoperta da Jacques Binet: \[F(n) = \frac{\varphi^n - (1-\varphi)^2}{\sqrt{5}}\] La scoperta del numero aureo viene tradizionalmente associata al pitagorico Ippaso di Metaponto ed è legata allo studio del pentagono regolare. In particolare il numero aureo viene definito come il rapporto tra una diagonale del pentagono e un suo lato. Il fatto che il pentagono fosse una figura geometrica dagli attributi praticamente mistici per i pitagorici⁽¹⁾, ha reso lo stesso $\varphi$ un numero di una certa importanza, tanto che gli antichi greci pensavano che le proporzioni perfette, quelle del bello, fossero legate esattamente al valore di tale numero $\varphi$.
E spero sinceramente che ciò possa rispondere alla prima curiosità sul perché il numero aureo è perfetto.

Modelli atomici

Nell'ormai morto sito dedicato al breve documentario scientifico Powers of ten erano presenti alcuni modelli matematici sulla struttura della realtà. Seguendo lo spirito originario degli autori, Charles e Ray Eames, era presente anche il famoso modello planetario di Johannes Kepler basato sui solidi platonici e pubblicato sul trattato Mysterium Cosmographicum:

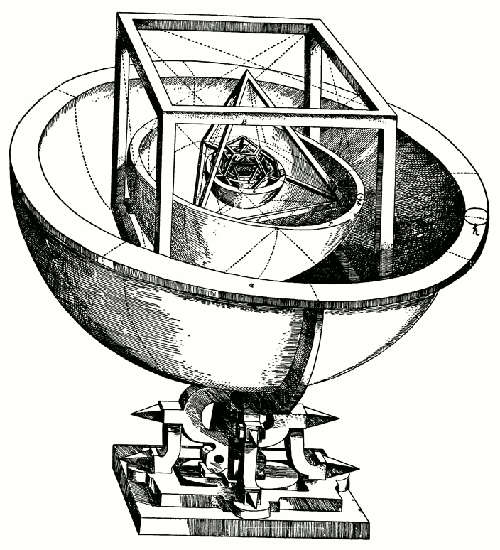Ingrandendo la parte centrale del modello si ottiene una visione di quello che si trova all'interno della terza sfera dell'immagine precedente, ovvero i pianeti più interni:

Da Kepler e dal sistema solare saltiamo al micromondo degli atomi con Lord Kelvin e al suo modello atomico a vortici⁽¹⁾, che, seppure errato, abbe il cantaggio, come ricorda Frank Wilczek, di dare origine alla teoria topologica dei nodi.