Ferguson è, infatti, il detentore del record di cifre decimali corrette del pi greco determinate con il calcolo manuale: ben 620 ottenute nel 1946. L'anno dopo, nel 1947, dopo aver scoperto un errore nella 528.ma cifra decimale tra quelle calcolate da William Shanks nel 1853, portò le cifre decimali fino a 710 a gennaio e quindi a 808 a settembre(1). In quest'ultimo caso con l'assistenza di J.W. Wrench jr e usando la formula di Machin e, soprattutto, una calcolatrice(2).
Lo stesso Wrench, insieme con Levi B. Smith, sempre facendo uso di una calcolatrice, portò il record nel 1949 a 1120 cifre decimali(1).
Il record successivo, 2037 cifre determinate quello stesso anno, ci porta nell'era del calcolo informatico. A portare a compimento il risultato fu, infatti, il team guidato da G. W. Reitwiesner usando ENIAC, Electronic Numerical Integrator and Computer, il quarto computer elettronico e il primo personal computer propriamente detto. Un numero di Liouville, così chiamato dal matematico francese Joseph Liouville, è un numero reale con una proprietà particolare. Per ogni numero intero positivo \(n\), esiste una coppia di interi \((p,q)\), con \(q > 1\), tali che \[0 < \left|x-\frac{p}{q}\right| < \frac{1}{q^{n}}\] Nel 1844 lo stesso Liouville dimostrò che tutti i numeri di Liouville sono trascendentali, mostrando per la prima volta l'esistenza di tali numeri. E visto che (\pi) è un numero trascendentale, è abbastanza ovvio chiedersi se sia anche un numero di Liouville. La risposta arriva nel 1953 grazie al matematico tedesco Kurt Mahler(1). Ed è negativa.
E visto che ci sono, neanche \(e\), il numero di Nepero, è un numero di Liouville. Il valore di pi greco può essere anche ricavato sperimentalmente. Se l'operazione più semplice e immediata è quella di misurare un oggetto circolare facendo poi il rapporto tra circonferenza e diametro, con relativi errori, un sistema più interessante soprattutto da portare in classe è quello proposto da Unofre Pili(3).
L'idea è piuttosto semplice. Se prendiamo un foglio di carta risulta molto più semplice utilizzare la densità superficiale in luogo di quella usuale. In questo caso la densità superficiale sarà, evidentemente, definita come il rapporto tra la massa e la superficie del foglio: \[\sigma = \frac{m}{A}\] Questo vuol dire che possiamo ricavare l'area all'interno di una circonferenza disegnata su un foglio di carta usando la relazione \[A_c = \frac{m_c}{\sigma}\] che poi può essere confrontata con la formula matematica della superficie di un cerchio \[A_c = \pi r^2\] A partire da queste basi matematiche si può eseguire il semplice esperimento.
Innanzitutto si disegnano sulla metà superiore di un foglio cinque circonferenze concentriche e in quella inferiore due triangoli come due metà di un rettangolo:
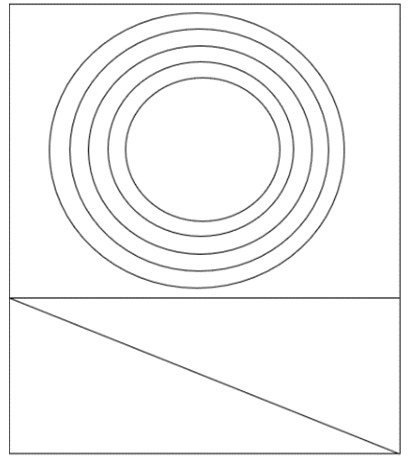
Veniamo ora all'operazione più delicata: ritagliare le figure. Personalmente, per ridurre al minimo possibile errori derivanti da questa operazione, consiglierei di usare un taglierino.
Fatto ciò si utilizzano i due triangoli per determinare la densità superficiale del foglio. In questo caso vanno misurate le dimensioni per ricavare la superficie e pesati i due triangoli. Più che usare un unico triangolo, meglio usarli entrambi: l'importante, ad ogni modo, è avere un minimo di cinque misure da cui ricavare un valore medio per \(\sigma\).
A questo punto si possono pesare i cinque cerchi e ricavare l'area usando la formula empirica, quella con la densità superficiale, e realizzare un grafico come quello di sotto mettendo in corrispondenza di ciascun raggio, il valore dell'area. Si otterrà una figura molto simile a una retta, entro gli errori sperimentali, la cui pendenza corrisponderà al valore del \(\pi\).

Tra l'altro la stessa cosa può essere eseguita con gli ellissi, ricordando che la formula della superficie di un ellisse è data da \[A_e = \pi a b\] dove \(a\), \(b\) sono le lunghezze dei due semiassi.
- Cronology of computation of pi ↩︎ ↩︎ ↩︎
- Newton's approximation of pi. Presentazione di Sarah Riffe e Jen Watt (pdf) ↩︎
Pili, U. B. (2022). Rapid estimation of π by weighing triangles, circles, and ellipses. Physics Education, 57(2), 025025. doi:10.1088/1361-6552/ac45c8 ↩︎



Nessun commento:
Posta un commento