Il corpo senza organi è un uovo: è attraversato da assi e soglie, con latitudini e longitudini e linee geodetiche, attraversato da sfumature che segnano le transizioni e il divenire, le destinazioni del soggetto in via di sviluppo lungo questi vettori particolari.Ed è incredibile, al di là della geniale associazione che ne fa la stessa en.wiki, notare come questa descrizione dell'uovo sia così aderente a quella, scientificamente precisa, di M. J. Schleiden in Das Meer.
Stomachion
domenica 31 marzo 2013
Corpo senza organi
Il corpo senza organi è un concetto sviluppato dal filosofo francese Gilles Deleuze e dal suo collaboratore Felix Guattari. In particolare ne L'antiedipo i due scrivono:
sabato 30 marzo 2013
Gente che...
Gente che non ha votato per Renzi alle primarie ma adesso è tutto un "se ci fosse stato Renzi..."
— Ermanno Ferretti (@scrip) March 29, 2013
Gente che ha votato Berlusconi per farsi togliere l'IMU e scopre che quello c'ha in mente solo i processi e la presidenza della Repubblica
— Ermanno Ferretti (@scrip) March 29, 2013
Gente che ha votato i 5 stelle per cambiare le cose e mandare i politici a casa e quelli dicono che vogliono tenere su il governo Monti
— Ermanno Ferretti (@scrip) March 29, 2013
Il vangelo proibito
Paragonare uno scrittore a Dan Brown, visto il successo internazionale di quest'ultimo, vuole essere un gesto carino e un modo sintetico per raccontare come questo autore abbia uno stile fluido e scriva delle storie appassionanti. Eppure David Gibbins (www.davidgibbins.com) è sicuramente di un'altra categoria rispetto a Brown. Le trame di quest'ultimo sono tanto semplici e lineari, quanto complesse e ricche di sorprese lo sono quelle di Gibbins. Certo potreste obiettare che il mio giudizio, basato su un unico romanzo, Il vangelo proibito, non è proprio attendibile, ma difficilmente un autore torna a scrivere un terzo romanzo con uno stile completamente diverso rispetto a quelli precedenti, a maggior ragione se sta scrivendo una vera e propria serie con personaggi ricorrenti. I due protagonisti, una sorta di Holmes e Watson dell'archeologia, sono Jack Howard, probabilmente un alter ego dello stesso Gibbins, anch'egli archeologo subacqueo come ricorda lo stesso scrittore nell'appendice al romanzo, e Costas Kazantakis, ingegnere.
I due protagonisti sono impegnati al largo della Sicilia, dove stanno esaminando il relitto sommerso di una vecchia nave romana del periodo di Claudio. L'ispirazione per questa parte iniziale dell'avventura viene a Gibbins da una spedizione reale che egli stesso ha diretto a Plemmirio, al largo di Capo Murro di Porco. Altri dettagli dello stesso ritrovamento descritto nel romanzo, invece, sono pescati qua e là sempre da spedizioni condotte sul campo dallo stesso ricercatore.
Non solo: anche le immersioni nel vecchio sistema fognario romano, quello della Roma Antica, per intenderci, è ispirato alle indagini condotte da un gruppo di speleologi urbani,come li definisce Gibbins, che hanno tracciato la mappa della Cloaca Massima. Inoltre i templi e le camere sotterranee a Roma descritti nel romanzo esistono realmente, o quasi:
I due protagonisti sono impegnati al largo della Sicilia, dove stanno esaminando il relitto sommerso di una vecchia nave romana del periodo di Claudio. L'ispirazione per questa parte iniziale dell'avventura viene a Gibbins da una spedizione reale che egli stesso ha diretto a Plemmirio, al largo di Capo Murro di Porco. Altri dettagli dello stesso ritrovamento descritto nel romanzo, invece, sono pescati qua e là sempre da spedizioni condotte sul campo dallo stesso ricercatore.
Non solo: anche le immersioni nel vecchio sistema fognario romano, quello della Roma Antica, per intenderci, è ispirato alle indagini condotte da un gruppo di speleologi urbani,
venerdì 29 marzo 2013
Jodorowski: Megalex

Se restiamo nel campo dei supereroi da un lato, concentrandoci magari su autori come Alan Moore, Warren Ellis, Grant Morrison, e del cyberpunk dall'altro l'autore probabilmente di riferimento principale in assoluto è Philip K. Dick, in pratica precursore del cyberpunk, che verrà codificato decenni dopo da due scrittori come William Gibbons e Bruce Sterling. Le sue invenzioni letterarie sono finite inevitabilmente nelle opere di Moore e quindi di Ellis e Morrison: visioni del futuro grazie alle quali plasmare il presente (forse...); esseri quasi onnipotenti eppure estremamente vulnerabili, come Palmer Eldrich; androidi che si ribellano alla programmazione e iniziano a sostituirsi agli esseri umani. Molto e molto altro ancora di queste idee e spunti sono finiti nelle storie degli sceneggiatori qui citati e in altri ancora.
L'autore di fumetti (ma non solo) che è probabilmente il più dickiano di tutti è, però, Alejandro Jodorowski, sceneggiatore che con le sue visioni ha reinterpretato molti generi disparati, un po' come lo scrittore pulp per eccellenza, Joe Lansdale, e in particolare il genere fantascientifico.
In particolare Megalex, una trilogia disegnata da Fred Beltran e recentemente pubblicata in un unico volume dalla Magic Press, è una visione di stampo ecologista dove sull'omonimo pianeta gli abitanti, sotto il controllo di una triade di regnanti spietati, hanno costruito un'unica e sempre più grande città, mentre i ribelli a questo regime si rifugiano nei sotterranei del pianeta e nell'unica foresta ancora rimasta, intorno all'albero più antico di tutta Megalex. La struttura sociale, poi, è abbastanza semplice: per mantenere il controllo sulla popolazione da parte dei tre regnanti (padre, madre e figlia), tutti gli abitanti indossano alla base del collo un dispositivo elettronico che, in base alla casta di appartenenza, esplode dopo un certo tempo di vita del soggetto.
giovedì 28 marzo 2013
Recami racconta Majorana

Così, come nell'articolo sopra citato, Recami, dopo aver mostrato Majorana, ne mostra la numerosa famiglia partendo dal capostipite, il nonno Salvatore Majorana, laureato in economia, professore ordinario presso l'Università di Messina e successivamente di Catania, ha retto il ministero di Agricoltura, Industria e Commercio nel primo e nel terzo governo Depretis. E sotto l'incarico di ministro ha anche fornito una citazione interessante che, in un certo senso, ha segnato la sua famiglia fino al nipote Ettore:
è lo sprezzo dei dettami scientifici - che in conclusione dovrebbero essere nel campo delle cose legislative quello che nelle applicazioni tecniche sono i teoremi della fisica e del calcolo, - codesto sprezzo, codesto divorzio tra il pensiero e la pratica, tra la scienza e l’arte sociale, la causa potente del disagio in cui la cosa pubblica si trovaFigli di Salvatore e Rosa Campisi furono Giuseppe, Angelo, Quirino, Dante, Fabio Massimo (padre di Ettore), Elvira ed Emilia. In particolare Quirino si laureò a 19 anni in ingegneria e a 21 in fisica, quando inizia anche ad avere i primi incarichi di insegnamento accademico. Se vi sembra una carriera precoce, tra l'altro non molto diversa da quella del padre di Ettore, Fabio (anch'egli a 19 anni laureato in ingegneria e a 21 in fisica), che ha anche fondato la prima società telefonica italiana, cosa direte mai della carriera di Angelo? Quest'ultimo, infatti, ottiene la maturità a 12 anni e la laurea in Legge a 16, ricevendo i primi incarichi di insegnamento a 17 anni, ben prima della maggiore età, all'epoca fissata ai 21 anni. E' a questo punto che Recami piazza una delle sue bordate politiche che, tra il serio e il faceto, alleggeriscono un po' la serata:
A quel tempo i ministri non volevano farci da genitori e lasciavano più libertà e quindi, per esempio, ci si poteva laureare anche a 12 anni

lunedì 25 marzo 2013
La natura ama nascondersi

Si inizia con alcune citazioni significative, partendo dal grande Galileo e da un passaggio tratto da Contro il portare la toga:
Perché, secondo l'opinion mia, a chi vuol una cosa ritrovare, bisogna adoperar la fantasia, e giocar d'invenzione, e 'ndovinareL'importanza della citazione sta proprio nel sottolineare come, a dispetto di quel che si crede, per comprendere come la natura funzioni è necessaria una certa dose di inventiva e di fantasia. In fondo per risolvere dei problemi, siano essi tecnici o matematici, è necessario cercare di inventare nuovi metodi per arrangiare i dispositivi di rilevazione (quando non costruirli da zero!) o combinare tecniche di calcolo matematiche apparentemente differenti una dall'altra.
D'altra parte il lavoro dello scienziato è anche un certosino esame di tesi e ipotesi in modo da stabilire, con la migliore approssimazione possibile, quello che sta avvenendo, come ben riassume sir Arthur Conan Doyle per bocca del suo ben noto personaggio, Sherlock Holmes:
It is an old maxim of mine that when you have excluded the impossible, whatever remains, however improbable, must be the truth.Tratta dal racconto L'avventura del diadema di berilli (The Adventure of the Beryl Coronet) è emblematica proprio dell'atteggiamento con cui porsi di fronte al bosone di Higgs, la cui esistenza era ritenuta da molti impossibile, ma che alla fine si è rivelato, per quanto improbabile, piuttosto reale!
Reseghetti, ad ogni, modo, nonostante sia visibilmente stanco, cerca di tenere desta l'attenzione (cosa in ogni caso difficile quando si sta parlando a diciottenni che vengono ad ascoltarti soprattutto per dovere e non per scelta) e sembra quasi che voglia riprendere gli studenti quando, a un certo punto, dopo un attimo di silenzio da parte sua, dice qualcosa del tipo:
Come capite che io sono qui e che vi sto parlando di fisica?Attraverso la vista e l'udito: sono queste le timide risposte e sono questo il genere di interazioni che ci permettono di sperimentare e interagire con il mondo circostante. Ed è proprio lo studio delle interazioni fondamentali uno dei punti più importanti dell'indagine fisica.
Labels:
bosone di higgs,
conferenze,
fisica,
franco reseghetti,
lhc,
liceo cavalleri,
milano,
parabiago,
scuola
domenica 24 marzo 2013
Reticolo matematico: la soluzione
Squillino le trombe, rullino i tamburi, ecco a voi la soluzione! L'ha fornita Popinga nei commenti al post in cui proponevo il rompicapo ed è assolutamente corretta:
 In attesa che mi decida sul prossimo quesito da proporvi, c'è il quizzino della domenica di .mau.
In attesa che mi decida sul prossimo quesito da proporvi, c'è il quizzino della domenica di .mau.

Conquistatore dello spazio
Attenzione: post aggiornato dopo la prima pubblicazione. Modificata la foto e aggiunti i link
Forse questa pubblicità l'avrete vista su un famoso antro atomico, che ogni tanto le propone, ma mi sembrava troppo bella per non proporvela a mia volta.
Ovviamente il pensiero va immediatamente a Wernher von Braun, l'uomo che ha permesso agli Stati Uniti di vincere la corsa verso la Luna contro l'Unione Sovietica. E il giocattolo appartiene proprio a quell'epoca: la pagina, infatti, è tratta da Topolino n.707 del 15 Giugno 1969, che un mio ormai ex-allievo mi ha portato un paio di mesi fa.
Forse questa pubblicità l'avrete vista su un famoso antro atomico, che ogni tanto le propone, ma mi sembrava troppo bella per non proporvela a mia volta.
Ovviamente il pensiero va immediatamente a Wernher von Braun, l'uomo che ha permesso agli Stati Uniti di vincere la corsa verso la Luna contro l'Unione Sovietica. E il giocattolo appartiene proprio a quell'epoca: la pagina, infatti, è tratta da Topolino n.707 del 15 Giugno 1969, che un mio ormai ex-allievo mi ha portato un paio di mesi fa.
venerdì 22 marzo 2013
Giornata internazionale dell'acqua 2013
La scuola non serve solo per imparare o insegnare, ma anche per tenersi informati:
E a proposito dell'acqua, c'è un'ottima raccolta di risorse sul Carnevale della Chimica #3.
giovedì 21 marzo 2013
Giocare con Mathics
Visto che il programma di 5.a liceo per matematica prevede lo studio di funzioni, ho deciso di divertirmi un po' con Mathics e con le funzioni che ho proposto/proporrò alla 5.a che mi è toccata nella nuova supplenza. Ed eccovi un po' di funzioni con i corrispondenti grafici prodotti con l'alternativa (on-line) a Mathematica:
\[f(x) = (x^2 + x) \ln |x|\]


martedì 19 marzo 2013
lunedì 18 marzo 2013
Scrivere ritratti
Ci sono alcuni momenti veramente geniali, come solo Stefano Benni li riesce a scrivere. Altri in cui sembra che sia proprio lì, dietro l'angolo, il colpo di genio, ciò che ti fa spanciare dalle risate per un minuto buono prima di riprendere la lettura. E forse il problema del libro è proprio quello: che sembra il peggior romanzo mai scritto da Stefano Benni.
Ma poi lo chiudi, leggi il nome sulla copertina, che non è Stefano Benni, e tiri un sospiro di sollievo.
P.S.: in effetti la seconda parte del libro propone dei passaggi gradevoli, ma mettete da conto che il giudizio potrebbe essere influenzato dal fatto che il protagonista è un uomo che, abbandonata l'attività di romanziere, inizia a scrivere ritratti. Come si fa qui.
Ma poi lo chiudi, leggi il nome sulla copertina, che non è Stefano Benni, e tiri un sospiro di sollievo.
P.S.: in effetti la seconda parte del libro propone dei passaggi gradevoli, ma mettete da conto che il giudizio potrebbe essere influenzato dal fatto che il protagonista è un uomo che, abbandonata l'attività di romanziere, inizia a scrivere ritratti. Come si fa qui.
venerdì 15 marzo 2013
Una (sempre troppo) breve storia del pi greco
Mi sembrava giusto estrarre le "notizie pi greche" che ho disseminato all'interno del Carnevale #59 e dedicare loro un post apposito, come ho fatto su Doc Madhattan. A maggior ragione mi sembrava giusto perché in questo modo mi posso sentire più libero di inserire gli script di aggregazione (automatica su Mathblogging e manuale su Researchblogging). E quindi ecco il motivo di un post che, in parte, è un doppio di quanto già scritto sempre qui:
Non ci sono prove esplicite del fatto che, all'epoca, la matematica egiziana fosse venuta a conoscenza di un numero come il $\pi$, però, tra i 600 e i 1000 anni più tardi su una tavoletta babilonese viene geometricamente stabilito il primo valore di $\pi$: $25/8 = 3.1250$. Da documenti redatti più o meno nello stesso arco di tempo si deduce poi che anche gli egiziani erano arrivati al calcolo del valore di $\pi$, ottenendo $(16/9)^2 ≈ 3.1605$.
La matematica indiana, invece, sembra leggermente in ritardo, visto che nel 600 a.C. nelle Shulba Sutras, si calcola per $\pi$ un valore di $(9785/5568)^2 \simeq 3.088$, che verrà successivamente aggiornato nel 150 a.C. come $\sqrt{10} \simeq 3.1622$, che è un valore molto più vicino a quello calcolato dagli egiziani.
Un valore molto vicino a quello oggi noto è invece quello calcolato da Rabbi Nehemiah nel suo trattato geometrico Mishnat ha-Middot, dove, correggendo il valore presente in un passo della Bibbia che indicava in 3 il valore del $\pi$, trova $3 + 1/7 \simeq 3.14286$.
L'approssimazione però più stupefacente non solo per la precisione ma soprattutto per il metodo è quella proposta da Archimede, il matematico italo-greco che ideò il metodo dei poligoni per calcolare quella che per un millennio divenne nota semplicemente come la costante di Archimede. Il nostro, semplicemente, calcolò il perimetro dei poligoni inscritti e circoscritti a una circonferenza data, ottenendo così una stima inferiore e una superiore al valore della costante: \[223/71 < \pi < 22/7\] ovvero \[3.1408 < \pi < 3.1429\] E' evidente che questo metodo di calcolo è estremamente moderno e soprattutto suggerisce come Archimede fosse ben conscio della natura trascendentale della costante, che poteva essere conosciuta solo attraverso delle approssimazioni.
Oggi il pi greco è noto fino a 5 trilioni di cifre (se non ce la fate ad andare così lontano, c'è il primo milione sul sito del Pi Day) e se provate a digitare il simbolo di $\pi$ sulle moderne calcolatrici scientifiche, il valore che esse vi forniscono è, per le prime cifre decimali, 3.14159265...
Come sapete il $\pi$ è definito come il rapporto tra la lunghezza della circonferenza e il suo diametro. Questo numero, che è trascendentale, visto che è impossibile ottenere contemporaneamente circonferenza e diametro interi, era, a quanto pare, noto fin dall'antichità. Ci sono, infatti, alcuni egittologi che ritengono che $\pi$, o forse $\tau = 2 \pi$ era loro noto, visto che il rapporto tra il perimetro e l'altezza della piramide di Giza, costruita tra il 2589 e 2566 a.C., è di 6.2857.
Non ci sono prove esplicite del fatto che, all'epoca, la matematica egiziana fosse venuta a conoscenza di un numero come il $\pi$, però, tra i 600 e i 1000 anni più tardi su una tavoletta babilonese viene geometricamente stabilito il primo valore di $\pi$: $25/8 = 3.1250$. Da documenti redatti più o meno nello stesso arco di tempo si deduce poi che anche gli egiziani erano arrivati al calcolo del valore di $\pi$, ottenendo $(16/9)^2 ≈ 3.1605$.
La matematica indiana, invece, sembra leggermente in ritardo, visto che nel 600 a.C. nelle Shulba Sutras, si calcola per $\pi$ un valore di $(9785/5568)^2 \simeq 3.088$, che verrà successivamente aggiornato nel 150 a.C. come $\sqrt{10} \simeq 3.1622$, che è un valore molto più vicino a quello calcolato dagli egiziani.
Un valore molto vicino a quello oggi noto è invece quello calcolato da Rabbi Nehemiah nel suo trattato geometrico Mishnat ha-Middot, dove, correggendo il valore presente in un passo della Bibbia che indicava in 3 il valore del $\pi$, trova $3 + 1/7 \simeq 3.14286$.
L'approssimazione però più stupefacente non solo per la precisione ma soprattutto per il metodo è quella proposta da Archimede, il matematico italo-greco che ideò il metodo dei poligoni per calcolare quella che per un millennio divenne nota semplicemente come la costante di Archimede. Il nostro, semplicemente, calcolò il perimetro dei poligoni inscritti e circoscritti a una circonferenza data, ottenendo così una stima inferiore e una superiore al valore della costante: \[223/71 < \pi < 22/7\] ovvero \[3.1408 < \pi < 3.1429\] E' evidente che questo metodo di calcolo è estremamente moderno e soprattutto suggerisce come Archimede fosse ben conscio della natura trascendentale della costante, che poteva essere conosciuta solo attraverso delle approssimazioni.
Oggi il pi greco è noto fino a 5 trilioni di cifre (se non ce la fate ad andare così lontano, c'è il primo milione sul sito del Pi Day) e se provate a digitare il simbolo di $\pi$ sulle moderne calcolatrici scientifiche, il valore che esse vi forniscono è, per le prime cifre decimali, 3.14159265...
giovedì 14 marzo 2013
Carnevale della Matematica #59

Il primo ospite da introdurre è inevitabilmente il numero di questa edizione, il 59, che è, udite udite, un bel numero primo, il 17.mo per la precisione, preceduto nella lista dal 53 e succeduto dal 61, di cui è il gemello. E come tutti i numeri primi non è solo un numero primo ma fa parte anche di un altro po' di club più o meno prestigiosi. Innanzitutto anche lui, come il 47, è un numero di Eisenstein. Questi numeri, come abbiamo visto un anno fa, sono dei numeri che possono essere anche complessi, visto che sono definiti come \[z = a + b \omega\] dove \[\omega = e^\frac{2i \pi}{3} = \frac{-1 + i \sqrt{3}}{2}\] e in particolare 57 può essere scritto con parte immaginaria nulla e parte reale pari a $3n + 1$. 59, però, è anche un numero di Pillai. Un numero primo $p$ è un numero di Pillai se esiste un intero $n > 0$ tale che il fattoriale di $n$, ovvero $n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n$, è inferiore di una unità rispetto a un multiplo di $p$, o detto in altri termini se $n! - 1$ è un multiplo di $p$. In particolare $15! - 1$ è divisibile per 59, e questo fa del nostro numero primo un numero di Pillai, nome che sta a ricordare il matematico Subbayya Sivasankaranarayana Pillai, che si interessò a questo genere di numeri, che tra l'altro sono infiniti, come è stato dimostrato da gente come Subbarao, Erdős, Hardy. Questo uno scorcio della loro lista:
23, 29, 59, 61, 67, 71, 79, 83, 109, 137, 139, 149, 193, ...
E' poi un numero primo regolare e supersingolare ed è anche un numero altamente cototiente. Un numero intero $k$ di questo genere è un numero per cui l'equazione
\[x - \varphi(x) = k\]
ha il numero di soluzioni maggiore rispetto a qualsiasi numero più piccolo, 1 escluso (visto che per 1 l'equazione ha un numero infinito di soluzioni). Si ricorda poi che $\varphi(x)$ è la funzione di Eulero, che quando $x$ è un numero primo $p$ assume questa forma:
\[\varphi(p^z) = (p-1) p^{z-1}\]
con $z > 1$.59 è poi un numero primo sicuro, non nel senso che è uno dei pochi numeri primi ad essere sicuro di essere un numero primo, ma nel senso che può essere scritto nella forma $2p + 1$, con $p$ a sua volta numero primo. Nel caso di 59 possiamo scrivere:
59 = 2 * 29 +1
con 29 a sua volta numero primo. Anche in questo caso eccovi l'inizio della lista:
5, 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, ...
Il 59, però, non ha ancora esaurito le curiosità matematiche: risulta, infatti, somma di tre numeri primi consecutivi, ovvero 17, 19 e 23, ed è anche il divisore del primo numero di Euclide $E_n$ a non essere a sua volta un numero primo.I numeri di Euclide sono così definiti: \[E_n = p_n \# + 1\] dove $p_n \#$, detto primordiale, è il prodotto di tutti i numeri primi fino a $p_n$, anch'esso primo (in un certo senso è l'equivalente del fattoriale ma solo per i numeri primi). Si osserva che i numeri di Euclide sono primi fino al sesto: \[E_6 = 30031 = 59 \cdot 509\] Infine da un icosaedro regolare si possono costruire 59 stellazioni (che potete produrre voi stessi con un progetto proposto su Wolfram Demonstations), dove per stellazione si intende un procedimento geometrico che permette di costruire a partire da una figura in 2 o in 3 dimensioni una nuova figura sempre in 2 o in 3 dimensioni.
Delle stellazioni dell'icosaedro, vi propongo la 59.ma secondo la classificazione proposta in The Fifty-Nine Icosahedra di H.S.M. Coxeter, P. DuVal, H.T. Flather, J.F. Petrie: Dopo aver ricordato che il praseodimio ha numero atomico 59, non mi resta che dare inizio alle danze!
mercoledì 13 marzo 2013
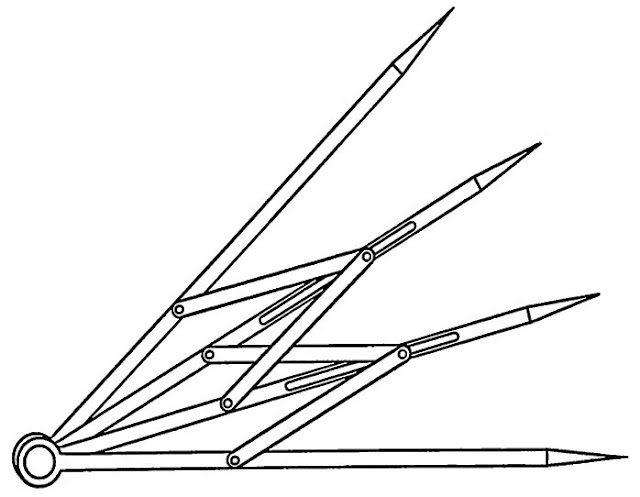
Reticolo matematico
martedì 12 marzo 2013
Dimostrazioni senza parole: Teoremi per trisecatori
Sulla trisecazione di un angolo
Rufus Isaacs. "Two Mathematical Papers without Words." Mathematics Magazine 48.4 (1975): 198
Rufus Isaacs. "Two Mathematical Papers without Words." Mathematics Magazine 48.4 (1975): 198
venerdì 8 marzo 2013
Il primo numero di Annals of Mathematics
A gennaio del 1874 faceva il suo esordio The Analyst, curato da Joel Hendricks, che nelle sue intenzioni sarebbe stata una pubblicazione di supporto per
Il suo posto viene preso da Annals of Mathematics, che di fatto è sempre The Analyst: ne prosegue, infatti, la linea editoriale espressa in quel primo numero del 1874. Dimostrazione di questo fatto è proprio il nuovo primo numero, datato Marzo 1884. Il suo sommario, infatti, inizia con un articolo astronomico di Asaph Hall: The Determination of the Mass of a Planet from the Relative Position of Two Satellites(2). Il punto di partenza è l'utilizzo della terza legge di Keplero per determinare la massa di un pianeta, di massa $m$ e con un satellite che gli ruota intorno, che ad esempio si muove intorno al Sole, di massa $M$ \[\frac{m}{M} = \frac{\tau_0^2}{\tau^2} \frac{a^3}{a_0^3}\] dove $\tau_0$, $\tau$ sono i periodi del pianeta e del satellite, e $a_0$, $a$ sono le distanze medie del pianeta dal Sole e del satellite dal pianeta. Ovviamente ci sarebbero da considerare alcune correzioni, come ad esempio il fatto che le orbite sono nella realtà ellittiche (anche se non di troppo). Ciò che però risulta interessante nell'articolo di Hall è che il suo obiettivo è quello di ridurre al minimo l'errore dovuto all'osservatore e senza dover necessariamente ripetere più volte la misura (che, secondo l'autore dell'articolo, non viene ridotto da questa buona pratica).
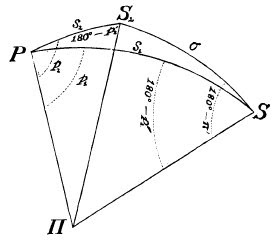 Il metodo proposto è quello sviluppato da Mr. Backlund, un astronomo dell'Osservatorio di Pulkowa che è sostanzialmente un metodo puramente geometrico che porta a un sistema di equazioni differenziali che risolvono il problema della determinazione della posizione esatta dei vari componenti del sistema fisico, dove $P$è il pianeta, $S_1$, $S_2$ i due suoi satelliti, $\Pi$ il polo celeste.
Il metodo proposto è quello sviluppato da Mr. Backlund, un astronomo dell'Osservatorio di Pulkowa che è sostanzialmente un metodo puramente geometrico che porta a un sistema di equazioni differenziali che risolvono il problema della determinazione della posizione esatta dei vari componenti del sistema fisico, dove $P$è il pianeta, $S_1$, $S_2$ i due suoi satelliti, $\Pi$ il polo celeste.
Si seguita a guardare sui cieli con la Luna, con la prima parte di un lavoro di tale G. W. Hill che si interessa delle influenze del moto dell'eclittica sul nostro satellite.
la presentazione e l'analisi di ognuna delle questioni di interesse o di importanza nella matematica pura e applicata, abbracciando in particolare tutte le nuove e interessanti scoperte nell'astronomia teorica e pratica, nella filosofia meccanica e nell'ingegneria.(1)Dopo un primo anno come mensile a 16 pagine, la rivista con l'anno successivo diventa bimestrale a 32 pagine, andando avanti così fino al novembre del 1883, quando esce il 6.o numero del 10.mo volume.
Il suo posto viene preso da Annals of Mathematics, che di fatto è sempre The Analyst: ne prosegue, infatti, la linea editoriale espressa in quel primo numero del 1874. Dimostrazione di questo fatto è proprio il nuovo primo numero, datato Marzo 1884. Il suo sommario, infatti, inizia con un articolo astronomico di Asaph Hall: The Determination of the Mass of a Planet from the Relative Position of Two Satellites(2). Il punto di partenza è l'utilizzo della terza legge di Keplero per determinare la massa di un pianeta, di massa $m$ e con un satellite che gli ruota intorno, che ad esempio si muove intorno al Sole, di massa $M$ \[\frac{m}{M} = \frac{\tau_0^2}{\tau^2} \frac{a^3}{a_0^3}\] dove $\tau_0$, $\tau$ sono i periodi del pianeta e del satellite, e $a_0$, $a$ sono le distanze medie del pianeta dal Sole e del satellite dal pianeta. Ovviamente ci sarebbero da considerare alcune correzioni, come ad esempio il fatto che le orbite sono nella realtà ellittiche (anche se non di troppo). Ciò che però risulta interessante nell'articolo di Hall è che il suo obiettivo è quello di ridurre al minimo l'errore dovuto all'osservatore e senza dover necessariamente ripetere più volte la misura (che, secondo l'autore dell'articolo, non viene ridotto da questa buona pratica).

Si seguita a guardare sui cieli con la Luna, con la prima parte di un lavoro di tale G. W. Hill che si interessa delle influenze del moto dell'eclittica sul nostro satellite.
giovedì 7 marzo 2013
Majorana, tra scienza e Pirandello
Attenzione: l'articolo è stato aggiornato dopo la sua pubblicazione iniziale con l'aggiunta delle informazioni sul conferenziere e i link di approfondimento.
Il 22 marzo 2013 alle 21 Erasmo Recami, sarà al liceo Ettore Majorana di Rho per parlare del grande fisico teorico cui è intitolata la scuola (dove sto facendo una supplenza di matematica) con una conferenza dal titolo:
Dramma umano di Ettore Majorana tra Pirandello e la rivoluzione scientifica degli anni 30
Recami è noto al di fuori dell'ambiente universitario per la biografia su Majorana: Il caso Majorana: epistolario, documenti, testimonianze. Ha poi raccolto tutti gli scritti e gli appunti majoraneschi nel volume Appunti inediti di Fisica teorica, curato insieme con Salvatore Esposito.
P.S.: al momento sono a scuola. Il post, quindi, verrà successivamente aggiornato il prima possibile.
Il 22 marzo 2013 alle 21 Erasmo Recami, sarà al liceo Ettore Majorana di Rho per parlare del grande fisico teorico cui è intitolata la scuola (dove sto facendo una supplenza di matematica) con una conferenza dal titolo:
Dramma umano di Ettore Majorana tra Pirandello e la rivoluzione scientifica degli anni 30
Recami è noto al di fuori dell'ambiente universitario per la biografia su Majorana: Il caso Majorana: epistolario, documenti, testimonianze. Ha poi raccolto tutti gli scritti e gli appunti majoraneschi nel volume Appunti inediti di Fisica teorica, curato insieme con Salvatore Esposito.
P.S.: al momento sono a scuola. Il post, quindi, verrà successivamente aggiornato il prima possibile.
mercoledì 6 marzo 2013
Un granello di tempo
A cavallo del secolo scorso, il Dottor Ward Wilmore lanciò una nuova teoria sul TEMPO.
Scrivendo isolato nella fredda eminenza del suo tetro castello, egli concluse che il TEMPO non era nulla più che un'altra forma di materia, una sottilissima sostanza filata intorno a noi come la tela di un ragno.
Egli sostenne inoltre che l'uomo passava attraverso la storia come se attraversasse una lunga serie di stanze, e che ogni cosa accaduta ieri è ancora qui, e tutto quello che ci accadrà domani esiste ed è in attesa del nostro arrivo.
La Terra in rotazione, egli credeva, è il veicolo. Se la Terra si dovesse fermare per un momento sul suo asse, potremmo semplicemente rivivere gli eventi di ieri. D'altra parte, se il globo dovesse girare più velocemente, il futuro si precipiterebbe su di noi come un'onda.
Per provare questo punto, egli costruì un pallone e si dispose a esplorare il futuro... Naturalmente non è più stato visto o udito da allora.
(Questa è la prima pagina della storia di Spirit del 2 marzo 1947. Tutte le storie del personaggio uscite sui giornali o sulle riviste della Quality sono, o dovrebbero essere in pubblico dominio, ed è con questo spirito che ho tradotto l'incipit della storia. Cliccando sull'immagine, potrete vedere la versione ingrandita con il testo leggibile della pagina. Per chi vuole leggere tutta la storia, c'è un file completo con solo la prima pagina a colori)
Scrivendo isolato nella fredda eminenza del suo tetro castello, egli concluse che il TEMPO non era nulla più che un'altra forma di materia, una sottilissima sostanza filata intorno a noi come la tela di un ragno.
Egli sostenne inoltre che l'uomo passava attraverso la storia come se attraversasse una lunga serie di stanze, e che ogni cosa accaduta ieri è ancora qui, e tutto quello che ci accadrà domani esiste ed è in attesa del nostro arrivo.
La Terra in rotazione, egli credeva, è il veicolo. Se la Terra si dovesse fermare per un momento sul suo asse, potremmo semplicemente rivivere gli eventi di ieri. D'altra parte, se il globo dovesse girare più velocemente, il futuro si precipiterebbe su di noi come un'onda.
Per provare questo punto, egli costruì un pallone e si dispose a esplorare il futuro... Naturalmente non è più stato visto o udito da allora.
(Questa è la prima pagina della storia di Spirit del 2 marzo 1947. Tutte le storie del personaggio uscite sui giornali o sulle riviste della Quality sono, o dovrebbero essere in pubblico dominio, ed è con questo spirito che ho tradotto l'incipit della storia. Cliccando sull'immagine, potrete vedere la versione ingrandita con il testo leggibile della pagina. Per chi vuole leggere tutta la storia, c'è un file completo con solo la prima pagina a colori)
martedì 5 marzo 2013
Fiamme

Intanto c'è questa intervista e questa iniziativa.
Immagine: Stefano Esposito
lunedì 4 marzo 2013
Ritratti: Ernst Mach
Nel 1911 John McGregor concludeva così la mini biografia uscita sull'Encyclopaedia Britannica:
Il principio si occupa dell'inerzia: partiamo da un secchio pieno d'acqua appeso a una corda a sua volta legata al soffitto. Se mettiamo in rotazione il secchio l'acqua al suo interno passerà dall'essere piatta nel caso del secchio fermo, al curvarsi nel caso del secchio in rotazione. In assenza dell'acqua un qualunque osservatore solidale con il secchio, come ad esempio una mosca seduta sul bordo superiore, potrebbe tranquillamente supporre che sia la stanza a ruotare e non il secchio stesso. Secondo Mach, però, questa discussione, che è una variazione su quanto scritto da Newton nei Principia, è incompleta a causa dell'assunto per nulla generale dello spazio assoluto. Bisogna quindi riformulare il principio di inerzia partendo dalla semplice osservazione del moto delle parti distanti dell'universo. In questo caso Mach propone il seguente cambio di paradigma: non più immaginare che sia un caso che la velocità di rotazione della Terra sia in accordo con le parti distanti dell'universo, ma suppore che le parti distanti dell'universo giocano un qualche ruolo nella formulazione delle leggi della meccanica locali(4).
O formulando il principio in una maniera più generale, proposta da Hawking e Ellis nel 1973:
Si può ben comprendere come Einstein fosse fermamente convinto del fatto che Mach sarebbe riuscito a scoprire la teoria della relatività ristretta con cinquanta anni di anticipo se solo la fisica avesse preso in seria considerazione la costanza della velocità della luce, sperimentalmente evidente già a quell'epoca.(2)
Ciò per cui è, però, soprattutto noto è il numero di Mach, che rappresenta il rapporto tra la velocità di un oggetto e la velocità del suono nel mezzo in cui quell'oggetto si sta muovendo: \[M = \frac{v_{\text{oggetto}}}{v_{\text{suono}}}\] Ad esempio Felix Baumgartner, nella sua caduta libera di ottobre 2012, ha raggiunto una velocità massima stimata di circa $370 m/s$ mentre si trovava all'interno della stratosfera(1). In questa porzione dell'atmosfera, caratterizzata da basse temperature a da bassa densità, la velocità del suono è fortemente influenzata dalle variazioni di temperatura, anche se si potrebbe stimare la velocità del suono in circa $300 m/s$ (poco più o poco meno) il che porta a un numero di Mach per Baumgartner di circa: \[M_B = \frac{370}{300} = 1.2\] o poco più.
Mach, però, come vedremo, si è interessato di diversi argomenti nella fluidodinamica, lasciando un segno decisamente indelebile. Nato il 18 febbraio del 1838 da Johann Mach e Josephine Langhans a Chirlitz-Turas, in Moravia, era, seguendo la sua stessa descrizione, un debole pietoso bambino che si è sviluppato molto lentamente(2). Il padre, che lavorava come istitutore presso una famiglia nobiliare, aveva studiato filosofia a Praga e si interessava di psicologia animale e agricoltura. Uno dei suoi risultati fu dare inizio alle colture di bachi da seta in Europa(2).
Nato il 18 febbraio del 1838 da Johann Mach e Josephine Langhans a Chirlitz-Turas, in Moravia, era, seguendo la sua stessa descrizione, un debole pietoso bambino che si è sviluppato molto lentamente(2). Il padre, che lavorava come istitutore presso una famiglia nobiliare, aveva studiato filosofia a Praga e si interessava di psicologia animale e agricoltura. Uno dei suoi risultati fu dare inizio alle colture di bachi da seta in Europa(2).
D'altra parte la madre era un'artista: musicista, disegnatrice, poetessa. E, come il padre, persona idealistica e solitaria(2): quel che si direbbe oggi nerd.
Tutta la sua teoria appare viziata dalla confusione tra fisica e psicologia.E potrebbe anche essere così, agli occhi di un suo contemporaneo, ma visto con gli occhi di oggi Ernst Mach è uno dei tanti geni che il passato ci ha regalato. E lo riteneva un genio, o comunque molto vicino ad esserlo, anche Albert Einstein, che riferendosi a se stesso diceva di essere uno studente di Mach. Quello che infatti lo stesso Einstein battezzò come principio di Mach, fu indubbiamente di grande importanza per lo sviluppo delle sue teorie relativistiche.
Il principio si occupa dell'inerzia: partiamo da un secchio pieno d'acqua appeso a una corda a sua volta legata al soffitto. Se mettiamo in rotazione il secchio l'acqua al suo interno passerà dall'essere piatta nel caso del secchio fermo, al curvarsi nel caso del secchio in rotazione. In assenza dell'acqua un qualunque osservatore solidale con il secchio, come ad esempio una mosca seduta sul bordo superiore, potrebbe tranquillamente supporre che sia la stanza a ruotare e non il secchio stesso. Secondo Mach, però, questa discussione, che è una variazione su quanto scritto da Newton nei Principia, è incompleta a causa dell'assunto per nulla generale dello spazio assoluto. Bisogna quindi riformulare il principio di inerzia partendo dalla semplice osservazione del moto delle parti distanti dell'universo. In questo caso Mach propone il seguente cambio di paradigma: non più immaginare che sia un caso che la velocità di rotazione della Terra sia in accordo con le parti distanti dell'universo, ma suppore che le parti distanti dell'universo giocano un qualche ruolo nella formulazione delle leggi della meccanica locali(4).
O formulando il principio in una maniera più generale, proposta da Hawking e Ellis nel 1973:
Le leggi fisiche locali sono determinare dalla struttura a grande scala dell'universo.Il principio venne originariamente formulato da Mach nel 1883 su Die Mechanik in ihrer Entwicklung historisch-kritisch dargestellt (La meccanica nel suo sviluppo storico-critico).
Si può ben comprendere come Einstein fosse fermamente convinto del fatto che Mach sarebbe riuscito a scoprire la teoria della relatività ristretta con cinquanta anni di anticipo se solo la fisica avesse preso in seria considerazione la costanza della velocità della luce, sperimentalmente evidente già a quell'epoca.(2)
Ciò per cui è, però, soprattutto noto è il numero di Mach, che rappresenta il rapporto tra la velocità di un oggetto e la velocità del suono nel mezzo in cui quell'oggetto si sta muovendo: \[M = \frac{v_{\text{oggetto}}}{v_{\text{suono}}}\] Ad esempio Felix Baumgartner, nella sua caduta libera di ottobre 2012, ha raggiunto una velocità massima stimata di circa $370 m/s$ mentre si trovava all'interno della stratosfera(1). In questa porzione dell'atmosfera, caratterizzata da basse temperature a da bassa densità, la velocità del suono è fortemente influenzata dalle variazioni di temperatura, anche se si potrebbe stimare la velocità del suono in circa $300 m/s$ (poco più o poco meno) il che porta a un numero di Mach per Baumgartner di circa: \[M_B = \frac{370}{300} = 1.2\] o poco più.
Mach, però, come vedremo, si è interessato di diversi argomenti nella fluidodinamica, lasciando un segno decisamente indelebile.

D'altra parte la madre era un'artista: musicista, disegnatrice, poetessa. E, come il padre, persona idealistica e solitaria(2): quel che si direbbe oggi nerd.
sabato 2 marzo 2013
Pasticciando in cucina: tortino di patate e zucchine
L'altra sera mia sorella mi chiede: cosa vuoi mangiare questa sera? E allora propongo patate e zucchine, da fare al forno, con rosmarino come sapore. Allora mia sorella, che ha deciso che non potevo cucinare io (per fortuna, visto l'ottimo risultato!) ha deciso non di fare una teglia con patate e zucchine sparpagliate lì, ma di realizzare dei tortini di patate e zucchine!
Ha utilizzato le mini teglie per le mini crostate dove ha messo uno strato di patate, uno di zucchine, uno di mozzarelle, uno di patate, uno di zucchine, uno di mozzarelle... in base a quanta roba entrava in ogni mini teglia (nessuna montagna, comunque!). Ovviamente ciascuna mini teglia unta con un cucchiaino di olio, e poi, una volta preparato, infornato il tutto a 180° per una quarantina di minuti circa.

 E il risultato, posso assicurarvelo, è stato ottimo!
E il risultato, posso assicurarvelo, è stato ottimo!


Ha utilizzato le mini teglie per le mini crostate dove ha messo uno strato di patate, uno di zucchine, uno di mozzarelle, uno di patate, uno di zucchine, uno di mozzarelle... in base a quanta roba entrava in ogni mini teglia (nessuna montagna, comunque!). Ovviamente ciascuna mini teglia unta con un cucchiaino di olio, e poi, una volta preparato, infornato il tutto a 180° per una quarantina di minuti circa.





Iscriviti a:
Post (Atom)