Le grandi domande della vita: Trova la funzione

A volte su quora spuntano domande che, in effetti, sono dei veri e propri esercizi delle scuole superiori, come quello che prevede di determinare il valore di una funzione, dati i valori precedenti: $$f(8)=56, f(7)=42, f(6)=30, f(5)=20, f(4)=12$$ L'obiettivo è determinare il valore di $f(3)$.
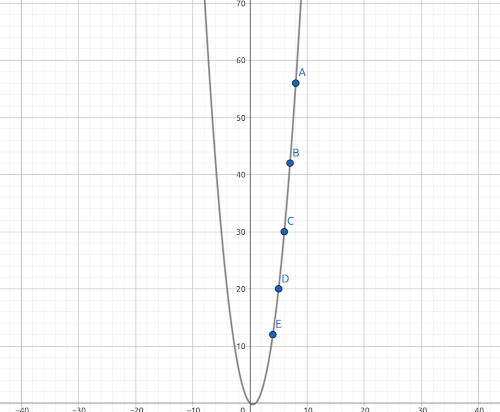
Se andiamo a vedere la sequenza delle risposte alla domanda, ne troviamo una inutilmente complicata e lunga. Il modo più semplice per risolverla, utilizzando la tecnologia moderna, è con geogebra, inserendo cioé i dati come punti del piano carteziano. In questo modo il software, con l'opportuno comando, è in grado di determinare la conica che passa per i 5 punti, ovvero $$y = x^2 -x$$ da cui $f(3) = 6$.
Un altro modo per risolvere, questa volta senza lausilio tecnologico, è osservare che $$f(8) = 56 = 8 \times 7$$ $$(7) = 42 = 7 \times 6$$ $$f6) = 30 = 6 \times 5$$ $$(5) = 20 = 5 \times 4$$ $$(4) = 12 = 4 \times 3$$ ovvero $f(n) = n \times (n-1)$ e quindi $$f(3) = 3 \times 2 = 6$$