Rompicapi di Alice: La spirale di Ulam

Mentre Stanislaw Ulam stava aspettando l'inizio di una conferenza presso i laboratori di Los Alamos, per passare un po' il tempo disegnò una griglia di linee orizzontali e verticali su uno dei fogli di appunti che si era portato dietro. Ulam, che era anche uno scacchista, all'inizio pensò di ideare un problema scacchistico, poi la sua mente andò in un'altra direzione e iniziò a scrivere all'intersezione delle linee un numero intero, partendo da 1 posto al centro della griglia.
Iniziò a disporli nella forma di una spirale e poi, una volta completata la griglia, iniziò a cerchiare i numeri primi, osservando come questi sembravano disporsi lungo linee dritte. Gli venne, così, in mente di capire cosa sarebbe successo riuscendo a realizzare una struttura con molti più punti all'interno della griglia.
Per fortuna di Ulam ai laboratori di Los Alamos erano dotati di un nastro magnetico (all'epoca i dati si registravano su delle bobine di pellicola dette nastri magnetici) su cui erano registrati i primi 90 milioni di numeri primi. Inoltre i ricercatori avevano a disposizione un supercomputer (super per l'epoca, ovviamente), MANIAC. Così, insieme con Myron Stein e Mark Wells, scrisse un programma per visualizzare sullo schermo del computer una spirale con tutti i numeri primi compresi tra 1 e 65000. Il risultato lo vedete nell'immagine qui sotto, tratta da The remarkable lore of the prime numbers di Martin Gardner, pubblicato nella sua rubrica dei Mathematical games su Scientific American 210:

Un'osservazione matematicamente interessante sulla spirale è legata a come si posizionano i numeri primi lungo le varie linee orizzontali, verticali e diagonali che si possono identificare all'interno della spirale di Ulam: secondo una distribuzione polinomiale.
La forma più generale delle varie distribuzioni è \[4n^2 + bn + c\] con \(b\), \(c\) costanti naturali.
Per esempio la linea passante per i numeri 5, 19, 41, 71, coincide con il polinomio \(4n^2 + 10n + 5\). La prima distribuzione polinomiale di numeri primi, \(n^2 - n + 41\), però, era stata scoperta da Leonhard Euler e può essere ritrovata all'interno di una variante della spirale di Ulam, il trinagolo di Klauber, scoperto nel 1931, ovvero 31 anni prima della spirale di Ulam, dall'entomologo Laurence Klauber . Nell'immagine qui sotto, tratta da commons, vediamo il triangolo con messa in evidenza in rosso la linea corrispondente alla distribuzione di Euler:

Fu lo stesso Klauber a notare tale associazione, come ben si evince dall'abstract del suo contributo al meeting della Southern California Section del 26 marzo del 1932:

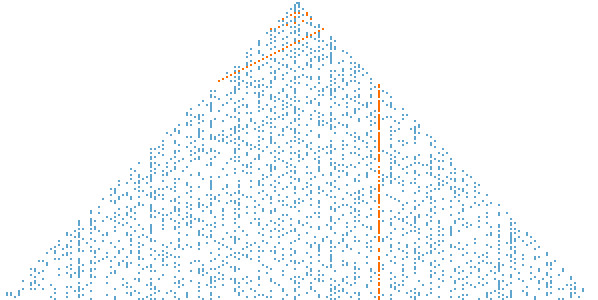
The integers are arranged in triangular order with 1 at the apex, the second line containing numbers 2 to 4, the third 5 to 9, and so forth. When the primes have been indicated, it is found that there are concentrations in certain vertical and diagonal lines, and amongst these the so-called Euler sequences with high concentrations of primes are discovered.

Per chi fosse interessato a graficare i numeri primi in forma spiraleggiante, consiglio di dare un'occhiata a Prime Visuals, che mette a disposizione un paio di pagine per giocare con la spirale di Ulam modificando alcuni parametri, quindi la guida per visualizzare i numeri primi in spirale usando Mathematica su Stackexchange, e infine il post Plotting Prime Numbers di Jake Tae.
Se qualcuno ci prova, mi faccia sapere: magari ci potrei scrivere un paralipomeno al riguardo!

• Daus, P. H. (1932), "The March Meeting of the Southern California Section", American Mathematical Monthly, 39 (7), Mathematical Association of America: 373–374, doi:10.1080/00029890.1932.11987331
• Stein, M. L.; Ulam, S. M.; Wells, M. B. (1964), "A Visual Display of Some Properties of the Distribution of Primes", American Mathematical Monthly, 71 (5), Mathematical Association of America: 516–520, doi:10.2307/2312588
• Gardner, M. (March 1964), "Mathematical Games: The Remarkable Lore of the Prime Number", Scientific American, 210: 120–128, doi:10.1038/scientificamerican0364-120