L'amplituedro e la cosmologia

Lo strumento matematico più potente sviluppato in fisica delle particelle per studiare le interazioni è il calcolo dello scattering, in termini meno tecnici la sezione d'urto. Nella visualizzazione delle interazioni introdotta dai diagrammi di Feynman, possiamo vedere un'interazione con un diagramma tipo quello qui sotto:

A sinistra ci sono le particelle che stanno per interagire una con l'altra, a destra i risultati dell'interazione, nel centro, nel cerchio grigio, l'interazione vera e propria. Il calcolo della sezione d'urto ci dice quale è la probabilità di avere certe particelle in uscita al posto di altre e quale velocità dovrebbero possedere. In base al tipo di interazione che avviene nella zona grigia, le probabilità di avere certi risultati piuttosto che altri risultano differenti e questo aiuta a capire, quindi, quali interazioni sono intercorse tra le particelle che hanno "urtato".
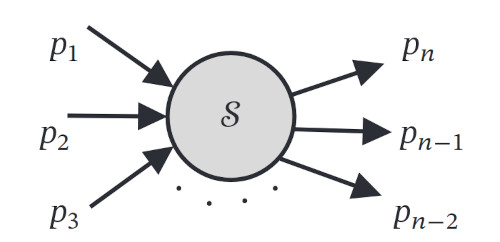
I diagrammi di Feynman sono risultati uno strumento estremamente utile per il calcolo delle sezioni d'urto, grazie a due vantaggi (che ho anche raccontato in altre occasioni). Innanzitutto per via della loro rappresentazione visuale delle interazioni. E poi perché le regole di Feynman, che si sono dimostrate compatibili con il modo usuale di eseguire i calcoli fino all'introduzione dei diagrammi, permettono di associare a ciascun elemento del diagramma un "pezzo" di matematica che poi effettivamente utilizzeremo per eseguire il calcolo.
Fino a qui una storia abbastanza consolidata. Senonché nel 2014 Nima Arkani-Hamed e Jaroslav Trnka non hanno introdotto l'amplituhedron, che potremmo rendere come l'amplituedro, ovvero un poliedro utilizzato per calcolare le ampiezze delle sezioni d'urto delle particelle: è, semplicemente, un approccio puramente geometrico, in cui la zezione d'urto è rappresentata da una forma geometrica dipendente dagli stati iniziale e finale delle particelle coinvolte. Il volume di questa forma geometrica fornirà l'ampiezza della sezione d'urto, ovvero, come detto all'inizio, la probabilità associata a quella specifica interazione di avvenire.
Se già questa è una proposta che trovo particolarmente interessante (anche alla luce dei lavori teorici su cui sono basati il trittico di articoli di cui ho scritto tempo fa), potete immaginare quanto interessante abbia trovato scoprire che negli ultimi anni è stato implementato un uso dei diagrammi di Feynman in cosmologia!
L'approccio è decisamente molto recente, come si vede dalla data di questo articolo sui cosiddetti correlatori cosmologici, e non ci sarebbe da stupirsi se presto verrà proposta anche un'applicazione degli amplituedri a questo campo recentissimo, visto che il primo autore dello studio è Nima Arkani-Hamed!
Ulteriori dettagli, incluse connessioni con la combinatoria, li potrete trovare nel completo (e in molti punti anche particolarmente tecnico) articolo di Claudia Fevola e Anna-Laura Sattelberger, Algebraic and Positive Geometry of the Universe: From Particles to Galaxies sulle Notices of AMS, una lettura sempre stimolante (quella della rivista) che ho deciso di riprendere a spulciare più spesso, come facevo ormai una decina di anni fa.