canta, canta, canta, canta all'alba
La
poesia gaussiana redatta con grande impegno da
Marco Fulvio Barozzi in arte
Popinga è una struttura poetico-matematica abbastanza semplice da comprendere. Una volta capito come si alternano i versi si può trasformare (quasi) qualisiasi numero in un verso partendo dalla sua fattorizzazione. E per il 176, numero d'ordine del Carnevale della Matematica che vi apprestate a leggere, la sua fattorizzazione è pari a
\[2^4 \times 11\]
per cui dall'unione dei versi corrispondenti ai "due" fattori, ecco il verso d'apertura della
special edition odierna.
Perché, come spero ricorderete (e l'orario di uscita del Carnevale è in questo un indizio significativo) oggi è il
pi day, che ormai dal lontano 2012 con l'
edizione #47 viene festeggiato qui su
DropSea.
Come è ovvio, quindi, il tema portante di questa edizione è proprio il
pi greco, che sarà protagonista non solo in alcuni dei contributi che mi appresso a presentare, ma anche grazie alle ormai usuali
notizie pi greche, i piccoli
box con i quali nel corso degli anni ho cercato di raccontare la storia e altre curiosità del numero più famoso del mondo. Per cui questa introduzione al Carnevale è dedicata al 176.
Questi è un
numero pari i cui divisori sono: 1, 2, 4, 8, 11, 16, 22, 44, 88, 176. Se li sommiamo insieme, 176 escluso, otteniamo 196, maggiore di 176, il che fa di quest'ultimo un
numero abbondante. Se però alla somma di prima togliamo il 4 e il 16 otteniamo proprio 176, il che lo rende un
numero semiperfetto.
Fa poi parte delle seguenti terne pitagoriche:
(57, 176, 185), (132, 176, 220), (176, 210, 274), (176, 330, 374), (176, 468, 500), (176, 693, 715), (176, 960, 976), (176, 1932, 1940), (176, 3870, 3874), (176, 7743, 7745)
proprio come il 167, ovvero il protagonista dell'
edizione 2023, è un
numero felice. E visto che vi voglio bene, invece di rimandarvi a quell'edizione, vi (ri)definisco qui la felicità:
Prendiamo un numero. Eleviamo al quadrato ciascuna delle sue cifre. Quindi sommiamole. Ripetiamo l'operazione con il risultato ottenuto. Proseguendo si può ricadere in due situazioni: il ciclo finisce con 1; il ciclo non finisce mai con 1 e, anzi, entra in un
loop. Nel primo caso il numero si dice felice. E questa è la felicità del 176:
\[1^2 + 7^2 + 6^2 = 86\]
\[8^2 + 6^2 = 100\]
\[1^2 = 1\]
Come qualcuno avrà notato, la cosa non poteva che essere così, visto che le cifre del 176 sono una delle possibili permutazioni delle cifre del 167!
Con le prossime due proprietà del 176 spero di non perdervi. Il 176, infatti, è un
numero pratico. Il motivo è che tutti i numeri interi positivi precedenti al 176 possono essere scritti come somma di uno o più dei suoi divisori.
E' interessante osservare come due particolari congetture sui numeri primi, la
congettura di Goldbach e la
congettura dei numeri primi gemelli, che non sono ancora state dimostrate per i numeri primi, si sono rivelate vere per i numeri pratici. In pratica ogni numero pari può essere scritto come la somma di due numeri pratici, ed esistono ifniniti numeri pratici (m) tali che anche (m+2) è un numero pratico (in realtà i numeri pratici si spingono addirittura fino a terne di numeri pratici gemelli!).
Infine il 176 è un
numero colombiano. Per spiegare cosa sono questi numeri faccio un esempio. Prendiamo il 43. Può essere scritto come 43 = 35 + 5 + 3. Notate che sia 5 sia 3 sono le cifre che compongono il 35. Ebbene il 43
non è un numero colombiano. Mentre, per esempio, il 42, o il
nostro 176,
è un numero colombiano poiché non esiste nessun intero positivo con il quale scrivere un'uguaglianza simile a quella scritta per il 43.
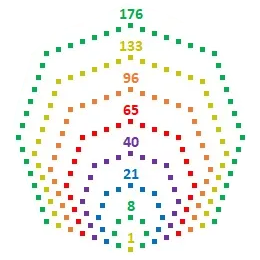
Lascio per ultima la proprietà che può essere rappresentata con una figura. Il 176, infatti, è un
numero ottagonale poiché può essere rappresentato come un ottagono: