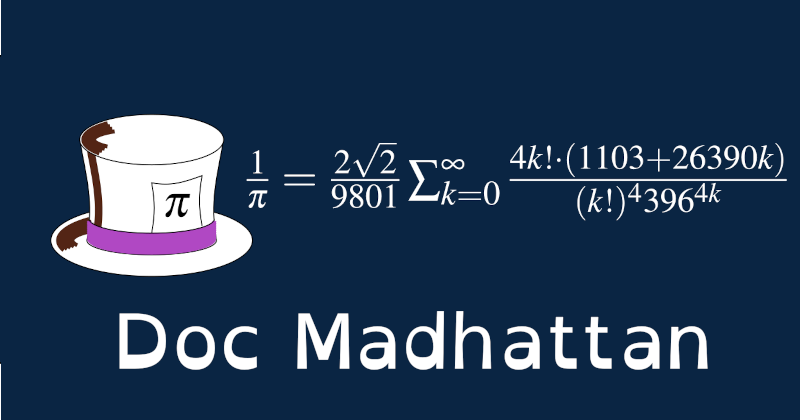Matematica, lezione 59: Teoria quantistica

Sebbene le questioni sull'interpretazione della meccanica quantistica vengano comunque citate, Teoria quantistica: basi matematice e concettuali di Marco Erba e Claudio Sutrini ci si sofferma il giusto tempo per introdurre il contesto, per poi approfondire gli aspetti più matematici della questione.
In particolare i due autori sviluppano un punto di vista particolare, quello dell'informatica quantistica, che occupa i due terzi del loro testo. In questo senso, sebbene si possa comunque considerare legittima la scelta, un po' come nel caso del volume dedicato a matematica e filosofia, si potrebbe obiettare che un titolo più centrato sulla teoria dell'informazione quantistica sarebbe stato più idoneo. Rispetto a quel volume, però, ci sono anche delle decise differenze, visto che al tempo stesso l'argomento viene ampiamente centrato e sviluppato in maniera oserei dire soddisfacente.
Tra l'altro viene anche citata la teoria delle categorie quantistica, con la sua nuova visione che potrebbe superare qualunque questione legata all'interpretazione della meccanica quantistica e che aveva già fatto capolino sul 48.mo volumetto della serie.
I due autori, poi, nella sezione dei giochi matematici propongono alcuni rompicapo di tipo statistico, a parte i primi due, abbastanza classici (uno, se non erro, anche riproposto da Maurizio Codogno in uno dei volumi precedenti). Infine Sara Zucchini ci racconta la vita di Stanislaw Ulam, matematico e fisico teorico che, tra le altre cose, lavorò anche al famigerato Progetto Manhattan.

Topolino #3618: Topolino indaga

Mentre la copertina di Davide Cesarello è dedicata ai pesci d'aprile, tema sviluppato in un articolo di Marco Travaglini, la storia d'apertura vede il ritorno della serie Topolino in giallo, nel corso della quale la coppia Topolino e Minni indaga in varie località del Calisota diverse sia da Topolinia sia (per ora) da Paperopoli.
Con Mistero a quattro corde Marco Bosco affiancato ai disegni da Carlo Limido, porta la coppia di fidanzati a Pleasantville mentre è in corso un festival di musica classica. L'indagine ruota apparentemente intorno alla sparizione di un violinista di fama mondiale che avrebbe dovuto suonare, nella serata inaugurale, un rarissimo Topolieri, che richiama alla memoria degli appassionati del genere il violinista e compositore italiano Antonio Salieri, che, tra le altre cose, fu anche maestro di Beethoven!

Absolute Power #1: Attacco ai supereroi

In un certo senso Beast World è stato una specie di prologo ad Absolute Power, non solo perché l'avversario dietro le quinte della sfida affrontata dai Titans è lo stesso, Amanda Waller, ma anche per alcuni dei temi di fondo di Beast World che, come vedremo, sono esplicitamente centrali in Absolute Power.
La storia, disegnata da un pulitissimo Dan Mora, disegnatore del Costa Rica che ricorda Mike Deodato jr. per il tratto e la gestione dei personaggi, vede il ritorno a un crossover DC Comics di Mark Waid, che in maniera più o meno esplicita aveva affrontato i temi che leggeremo sui quattro numeri in cui è pubblicata in altri suoi progetti, come per esempio Kingdom Come o, uscendo dall'ambito strettamente supereroistico, Empire.
La miniserie era stata anche anticipata da un albo speciale, Ground Zero, contenente alcune storie brevi che approfondivano alcuni aspetti preparatori al piano della Waller. Una di queste storie brevi era stata pubblicata nello speciale uscito a fine 2024 in occasione della Free comics week, mentre le altre hanno trovato spazio sul primo spillato dell'edizione italiana.
Ciascuna di queste storie, co-scritte da Waid (a parte una) insieme con altrettanti sceneggiatori e disegnatori, si concentrano ciascuna su un personaggio chiave della miniserie, preparando il terreno all'attacco totale che la Waller porterà a termine nel corso del primo numero.
Prima di lasciarvi alla recensione, vi ricordo che sul Cappellaio Matto c'è un piccolo approfondimento scientifico.

Gruppi quantistici e basi cristalline: il Premio Abel 2025

Masaki Kashiwara via Scientific American

Il Premio Abel 2025 è stato assegnato al matematico giapponese Masaki Kashiwara

per i suoi fondamentali contributi all'analisi algebrica e alla teoria delle rappresentazioni, in particolare per lo sviluppo della teoria dei D-moduli e la scoperta delle basi cristalline.

In particolare, queste basi cristalline (crystal bases in inglese: non ho trovato un modo migliore per tradurle) sono particolari strumenti utilizzati nella teoria delle rappresentazioni (non sfuggirà la coincidenza con i miei interessi di dottorato!) dei gruppi quantistici (e per estensione, anche per i gruppi di Lie). Per capire cos'è un gruppo quantistico, basta pensare alle simmetrie di un quadrato. Possiamo ruotarlo di 90 gradi, rifletterlo, e via discorrendo. Queste operazioni formano un gruppo in cui l'ordine in cui le operazioni vengono eseguite è importante (una rotazione poi una riflessione fornisce un risultato diverso da una riflessione seguita da una rotazione).

Una nuova casa per Doc Madhattan

L'ultimo post di Doc Madhattan, il mio blog in inglese ospitato dentro il blog network di Field of Science risale al 24 ottobre. Di questo post ne ho poi pubblicato a fine 2024 una versione in italiano, però gia in occasione di Scienza take away #4 avevo espresso l'intenzione di spostare il blog da un'altra parte per ovviare al problema del certificato di sicurezza non aggiornato. Prima di muovermi, avevo atteso un po' dopo l'invio di una e-mail al creatore e amministratore del network, ma in assenza di risposta ho iniziato a cercare più assiduamente un posto dove spostare Doc Madhattan.
Ho valutato diverse soluzioni, molte di queste molte raccolte in questo post di Hubspot, e tutte inevitabilmente scartate. Poi, giusto ieri, dopo aver valutato un trittico di proposte interessanti (le altre due sono WebWave e DevDojo: ve le segnalo se possono interessarvi), alla fine ho scelto Hashnode essenzialmente perché è presente, nel blog, una newsletter integrata.
Doc Madhattan ora lo trovate qui e, se vi va, potete anche iscrivervi alla newsletter. E come vedete ho anche già trasferito l'intero archivio (quasi, a dire il vero: solo un post non ho potuto trasferire) e questo grazie a un convertitore che mi ha permesso di esportare il backup di Blogspot nel formato markdown e quindi importarlo di massa su Hashnode. Non escludo che non tutto sia andato per il verso giusto, ma con calma proverò a sistemare le "magagne" man mano che ci capito.
In ogni caso ci sono anche un altro paio di vantaggi interessanti nell'essere andato su Hashnode: innanzitutto la possibilità di scrivere in markdown, quindi il supporto alle equazioni già integrato dentro la piattaforma, e infine la possibilità di fare un ulteriore backup online oltre alla classica esportazione utilizzando un repository su git-hub.
Spero, quindi, che questa nuova vita di un vecchio progetto possa ritagliarsi un suo spazio vivo e vitale!

L'Amleto, controcorrente

Sul Post hanno scritto un bell'articolo su Grand Theft Hamlet, un documentario piuttosto particolare, visto che è stato "girato" all'interno di GTA. Nell'articolo ho trovato un passaggio particolarmente interessante, che dice tanto non solo sul gioco, ma anche su noi stessi e sulla nostra società:

Una delle caratteristiche che conferiscono a Grand Theft Hamlet uno status diverso rispetto ad altri machinima è il modo in cui è montato e confezionato. Los Santos, la città fittizia di GTA V, è stata ideata e disegnata per essere una versione esagerata di Los Angeles, un luogo da cui emerge l’ossessione per il capitalismo, il denaro come unica forma di transazione e relazione, e in cui il crimine è la regola. Il fatto che in quel mondo un gruppo di persone cerchi di fare qualcosa che equivale a nuotare controcorrente, ovvero non sparare, scappare, rapinare e rubare veicoli ma mettere in scena uno spettacolo, e che debba ironicamente combattere contro il resto dei giocatori ignari del progetto, alla lunga induce lo spettatore a riflettere su temi di certo non inediti, come la difficoltà nell'aggregare persone, il desiderio di fare qualcosa di più delle proprie vite, le diverse maniere e ragioni per le quali le persone si approcciano all'arte o il contrasto con chi ha altre aspirazioni nella vita, ma in una maniera diversa dal solito.

In effetti abbiamo tanto bisogno di fare cose semplici, cose che oggi sono tremendamente controcorrente.

Matematica, lezione 58: Matematica senza i greci

Compendio ideale ai Sistemi di numerazione, Matematica senza i greci è un percorso storico che guida il lettore alla scoperta della matematica fatta da altri popoli oltre i greci.
In effetti, come spiega molto bene Paolo Caressa, la matematica su cui si basa quella che studiamo a scuola è sostanzialmente matematica ellenistica, ma a parte questa precusazione, l'autore ci conduce attraverso i continenti prima con i sumeri e gli egizi, quindi oltreoceano verso i Maya e gli Inca e infine in Cina e in India.
Ricco di curiosità, il volumetto, che sarebbe stato perfetto per chiudere la serie (ma così non è stato possibile), tratta, tra le altre cose, di teorema di Piragora e pi greco visti dai diversi punti di vista delle varie culture. E a proposito di pi greco, la parte principale del testo si chiude proprio con Madhavan di Sangamagrama e la scuola matematica indiana di Kerala di cui ho scritto nella puntata 2025 della Breve storia del pi greco.
Nella sezione biografica torna Sara Zucchini che ci racconta di due matematici italiani al tempo stesso molto diversi tra loro, ma anche con alcuni punti in comune: Lucio Lombardo Radice e Giorgio Israel. Nei giochi matematici, infine, Caressa prosegue con il tema principale del volume proponendoci un po' di matematica ricreativa... d'annata!

Breve storia del pi greco: Edizione indiana

Bentrovati alla puntata del 2025 della Breve storia del pi greco, una serie di articoli che "ristampano" i box delle notizie pi greche che dal lontano 2013 tediano allegramente i Carnevali della matematica del pi day che ho l'onore di ospitare. Come ormai dal 2020, un po' tutte le puntate hanno perso l'ordinale per un più pratico titolo che ne sintetizza i contenuti, e la cosa succede anche alle notizie pi greche estratte dal Carnevale della matematica #185, quello di quest'anno.
Prima di procedere con la lettura, c'è una novità: ho deciso, infatti, di raccogliere i post della serie in una pagina apposita, scelta più pratica del solito copia/incolla della lista completa:

Breve storia del pi greco: la serie completa

Come raccontato nell'ormai lontano Carnevale della matematica #59 (oppure nella prima puntata della Breve storia del pi greco), il moderno calcolo delle cifre decimali del $\pi$ si basa su una combinazione degli algoritmi iterativi con le serie rapidamente convergenti. La serie di record, ben 18, ottenuta dal matematico giapponese Yasumasa Kanada è stata possibile proprio grazie a questo genere di serie.
Le prime serie rapidamente convergenti sono dovute al Srinivasa Ramanujan, che nel 1914 pubblicò diverse di queste serie, tutte caratterizzate da una grande eleganza matematica e, soprattutto, dalla loro velocità nel convergere. Per esempio, una di queste formule, basata sulle equazioni modulari, è

Topolino #3617: Sulle tracce di Arcimboldo

Nella serie de La storia dell'arte di Topolino, Roberto Gagnor non aveva mai affrontato Giuseppe Arcimboldo, pittore rinascimentale italiano noto per i suoi ritratti composti con frutta e verdura. In effetti l'Arcimboldo era stato omaggiato sul lontano Topolino #2580 da Nino Russo e Ottavio Panaro con L'Arcinciccio, associando così il grande pittore al personaggio disneyano che più gli si avvicina: il buon Ciccio.
Questa scelta era così ottima che Gagnor, questa volta affiancato da Giampaolo Soldati, la ripercorre in maniera leggermente differente: lo spunto iniziale de La memoria ghiottona è la ricerca, da parte di Paperone, della ricetta di un antico additivo che rendeva i pasti della Lombardia rinascimentale particolarmente gustosi. E custode di questo segreto era Barmbillone degli Arciccioldi, versione disneyana dell'Arcimboldo. Così Paperone decide di tornare in Italia alla ricerca di questo sapurun avendo come guida un discendente degli Arciccioldi: potete solo immaginare in quali gag e situazioni divertenti verranno trascinati Paperone e Nonna Papera andando dietro alla ghiottoneria del buon Ciccio!

Classici Disney #545: PippoParodie

Post aggiornato dopo la prima pubblicazione con la sistemazione della formattazione.

---

A partire dal #72 de Le grandi parodie Disney, rivista che aveva ristampato in grande formato, spesso rimontandole, le parodie disneyane, la testata inizia a presentare una serie di storie denominate PippoParodie. Sotto questo cappello vennero stampate, e in alcuni casi ristampate, molte delle storie della serie Disney Goofy Classics, avventure di produzione Disney Studio in cui Pippo interpretava grandi classici della letteratura, ma anche eventi storici o personaggi famosi, gente come Galileo Galilei o Leonardo da Vinci, per dirne due, o capolavori come Frankenstein, reinterpretato con uno stile alla Mel Brooks.

Paralipomeni di Alice: MathGPT e il mah-jong

Grazie a un articolo su MaddMaths! relativo alla dimostrazione di Andrew Wiles sull'ultimo teorema di Fermat, ho recentemente scoperto l'interessante Lean, un proof assistant, ovvero una rete neurale specializzata nelle dimostrazioni matematiche. Non è ancora al livello di realizzare da zero una dimostrazione, o almeno così si dice, ma è un utile strumento per verificare i passaggi più ostici delle dimostrazioni. Ho provveduto a installarlo, ma ancora non l'ho provato.
Ho, invece, iniziato a provare alcune reti neurali conversazionali di tipo matematico. In effetti sono un po' più che semplici reti conversazionali, visto che sono in grado di risolvere equazioni, impostare dimostrazioni semplici, realizzare grafici e in alcuni casi, come quello di MathGPT, anche realizzare dei video.

Le grandi domande della vita: Ci serve veramente un'interpretazione fisica della meccanica quantistica?

Niels Bohr

Il 2025 è l'Anno Internazionale della Scienza e della Tecnologia Quantistica, per cui può essere interessante tornare sull'annosa questione dell'interpretazione di Copenaghen della meccanica quantisica. Partirei, prima di tutto dalla questione se effettivamente tale interpretazione ha un ampio consenso tra i fisici.
Ed effettivamente sia nel 1997, sia nel 2011 sono stati realizzati dei sondaggi tra i fisici teorici su quale fosse la loro interpretazione quantistica preferita. E la maggior parte dei fisici teorici hanno votato per l'interpretazione di Copenaghen.
I risultati ottenuti in due anni distinti e in due conferenze distinte in cui comunque, in totale, saranno stati presenti un'ottantina di fisici teorici, non possiamo comunque considerarli come indicativi di tutta la cateogria, ma possono fornire alcuni spunti interessanti. Se, infatti, sono sostanzialmente inutili quelli del workshop informale sulla meccanica quantisica UMBC dell'agosto 1997 (i cui risultati hanno permesso a Max Tegmark di "parlare" dell'interpretazione dei molti mondi in quello stesso articolo in cui discusse il suicidio quantistico), più interessanti sono i risultati ottenuti presso il workshop Quantum Physics and the Nature of Reality tenutosi nel 2011 presso la International Academy Traunkirchen in Austria e condotto da Maximilian Schlosshauer, Johannes Kofler e Anton Zeilinger (ricordo che quest'ultimo ha ottenuto il premio Nobel per la fisica nel 2022).

La politicizzazione della scienza

Tra i molti problemi del ritorno di Donald Trump sullo scranno di presidente USA, c'è anche quello della politicizzazione della scienza. Per cui ho pensato di proporvi un'edizione leggera e veloce sul tema costituita da un paio di articoli a tema, iniziando con:

Pielke Jr, R. A. (2004). When scientists politicize science: making sense of controversy over The Skeptical Environmentalist. Environmental Science & Policy, 7(5), 405-417. doi:10.1016/j.envsci.2004.06.004

Scienza take away #7: febbraio-marzo 2025

Avendo ospitato il Carnevale della matematica #185, quello dedicato al pi day, il mese precedente è stato per lo più fagocitato dal pi greco, quindi, in pratica, ci sono ben pochi articoli a tema scientifico da segnalare in questa nuova edizione, anche se spero che siano tutti particolarmente interessanti. Iniziamo.

Da DropSea

Con un po' di ritardo rispetto al Darwin day, il che è anche normale visto che ho assistito all'opera teatrale solo un paio di giorni dopo, esce la mia recensione di Darwin, Nevada, ultima fatica del sempre grande Marco Paolini, uno che la scienza a teatro l'ha portata in tempi decisamente non sospetti!

Matematica, lezione 57: Meccanica analitica

E' stato un tuffo nel passato il volume Meccanica analitica di Paolo Caressa, precisamente fino ai tempi dell'università quando ho affrontato il tema della lagrangiana in un intero corso della laurea in fisica. In effetti quel corso, a differenza del volume di Caressa, si silungava anche con il "raccontare" l'hamiltoniana, che invece Caressa tratta in poche pagine giusto per completezza. In ogni caso il volume, ricco di formule, ha il pregio di mostrare un approccio alla meccanica decisamente più formale e, appunto, analitico rispetto alla meccanica newtoniana e dovuto essenzialmente a Joseph-Louis Lagrange, ovvero il fisico torinese Giuseppe Luigi Lagrangia che a un certo punto della sua vita scelse la Francia come patria.
A tal proposito ho trovato una bella coincidenza la sovrapposizione tra la lettura di Caressa e il mio breve soggiorno a Torino in occasione dell'inaugurazione della mostra Macchine del tempo, alla sua seconda tappa nel giro dell'Italia dopo la prima installazione a Roma. E tra l'altro è stato anche bello ripassare, un po' casualmente devo dire, di fronte alla sua statua, notando quel La patria pose (se non ricordo male il testo) che un po' mi ha fatto sorridere, visto che è stato naturalizzato francese!

Topolino #3616: Lezione di giornalismo

I festeggiamenti per i 5 anni di storie di Area 15 proseguono con un vero e proprio piccolo crossover con Papersera News, la serie di Corrado Mastantuono che ha riportato i auge il quotidiano di Paperone ideato mezzo secolo fa da Dick Kinney e Al Hubbard.
Con Afida all'ultimo scoop, Mastantuono confronta la redazione del Papersera, ovvero Paperino e Paperoga (sostanzialmente una situazione non molto differente, anzi forse anche peggiore, rispetto a uno dei tipici giornali distribuiti gratuitamente nelle metro di Milano), con i ragazzi di Area 15, cercando di raccontare il confronto generazionale attraverso il mestiere del giornalista. La prima cosa che colpisce è il gergo da geek tecnologici che Mastantuono mette sul becco dei ragazzi, cosa che il lettore non deve pensare sia una generalizzazione di tutta la generazione, ma una semplice caratterizzazione particolarei di questo gruppo di ragazzi.

Cronache di un'era glaciale

La maggior parte dei Manga di Jiro Taniguchi che ho letto trattano di storie sostanzialmente del tempo presente o del passato più o meno recente. Il tema portante di molte di esse, però, è il rapporto dell'uomo con l'ambiente circostante, che sia la città, come per esempio ne L'uomo che cammina, o la natura, come in Seton ha poca importanza. Ci sono, però, un paio di opere che spiccano nella produzione di Taniguchi: Blanca e il suo seguito, I cani degli dei, una sorta di Richiamo della foresta con alcuni spunti fantascientifici, e Ice Age Chronicle of the Earth, l'opera più squisitamente fantascientifica nella vasta produzione del mangaka.

3.15: Le proprietà del #185

Come già l'anno scorso, anche quest'anno vi propongo il video dedicato alle proprietà del 185 e uscito in contemporanea con il Carnevale della Matematica #185. Buona visione!

Carnevale della Matematica #185: pi day 2025

Benvenuti all'edizione n. 185 del Carnevale della matematica, la manifestazione on-line che raccoglie i post matematici dei blogger italiani che partecipano all'iniziativa.
Oggi, tra l'altro, è un giorno speciale: il pi day, il giorno del pi greco, ovvero la Giornata internazionale della matematica. In questo giorno si organizzano molti eventi un po' in tutto il mondo, e qui trovate gli eventi italiani. Qui su questo blog, che ormai da anni ospita il Carnevale della matematica proprio in occasione del pi day, il tema portante sarà, come da tradizione, il pi greco, che sviluppo all'interno del post attraverso le notizie pi greche. Questi box, due o tre a edizione, si intercalano tra i contributi dei matematti sviluppando il tema portante, mentre nell'introduzione vado a riassumere alcune delle proprietà del numero corrispondente all'edizione. Cosa da cui non sfuggiamo nemmeno quest'anno!

Le proprietà del 185

La poesia gaussiana di Marco Fulviuo Barozzi, in arte Popinga, è una struttuta poetica generata in maniera abbastanza semplice. Partendo dal 2, il primo numero primo della lista, associa a ciascun numero primo un vorso costituito da una parola o da una combinazione di parole, mentre a ciascun verso associato a un numero non primo, i corrispondenti versi "primi" con le opportune ripetizioni in base, appunto, alla fattorizzazione di quel verso.
Questa semplice regola permette di ricavare il verso della poesia gaussiana per ciascun numero naturale, a meno di avere un verso associato a ciascun numero primo. Il problema dell'estensione originale di Popinga è che l'ultimo numero primo considerato è il 31, ma la fattorizzazione del 185, ovvero l'ordinale associato a questa edizione del Carnevale della matenatica è $$185 = 5 \times 37$$ per cui per generare il verso gaussiano associato a questa edizione era necessaria un'estensione di quelli che chiamo i "versi primi", estensione che trovate su questa pagina, ma che non è di mio pugno. A partire da questa estensione, il verso gaussiano risulta quindi:

tra i cespigli gorgheggiando

Se poi facciamo la somma dei suoi divisori, otteniamo 43 che è minore di 185, il che rende quest'ultimo un numero difettivo.
Una proprietà molto interessante del 185 è, però, quella di essere un semiprimo. Un numero, infatti, appartiene a tale famiglia se può essere scritto come prodotto di due numeri primi, non necessariamente distinti. Si potrebbe allora dire di primo acchitto che tutti i numeri naturali sono semiprimi. In realtà non è così. Prendiamo il 4, la prima potenza di 2. Esso è semiprimo poiché $4 = 2 \times 2$. Prendiamo la potenza di 2 successiva, 8. Possiamo scriverlo come prodotto di due numeri nel modo seguente $8 = 2 \times 4 = 4 \times 2$, solo che l'unico primo è il 2 mentre il 4 non è primo, e quindi 8 non è semiprimo.
Anche il 581, ovvero il 185 scritto invertendo l'ordine delle sue cifre, è semiprimo, il che rende il 185 (e il 581) un numero omirpimes.
Il 185, poi, è un numero 20-gonale, ovvero che può essere rappresentato attraverso un poligono di 20 lati opportuno, e fa parte delle seguenti terne pitagoriche:

(57, 176, 185), (60, 175, 185), (104, 153, 185), (111, 148, 185), (185, 444, 481), (185, 672, 697), (185, 3420, 3425), (185, 17112, 17113)

E a proposito di triangoli rettangoli l'ultima curiosità su cui voglio soffermarmi prima di lasciarvi ai contributi di questa 185.ma edizione è legata alla spirale di Teodoro, così chiamata in onore del matematico greco Teodoro di Cirene, il primo a realizzarla.
Tale spirale viene costruita a partire dal triangolo rettangolo isoscele con cateti pari a 1. Sull'ipotenusa di tale triangolo, si costruisce un nuovo triangolo rettangolo, in cui un cateto è l'ipotenusa del triangolo precedente, e l'altro è un cateto sempre di lunghezza 1. A partire dal triangolo così ottenuto se ne costruisce un altro nello stesso modo. E così via. La spirale originale, che permette in questo modo di disegnare le radici quadrate dei numeri naturali, secondo quanto tramandatoci da Platone, si ferma al 16.mo triangolo e, quindi, alla radice quadrata di 17. E se portiamo la spirale fino al quarto giro troviamo proprio 185 triangoli rettangoli.

Aspettando il pi day 2025: Ramanujan e il pi greco

Come antipasto per il Carnevale della Matematica #185 dedicato al pi greco vi propongo un video sulla quadratura del cerchio con, tra i protagonisti, il buon Srinivasa Ramanujan. In effetti questo video è la riedizione di un video precedente (trovate qui l'articolo ispirativo). Buona visione e a tra poco con il Carnevale della Matematica!

Rompicapi di Alice: Il sudoku e i quadrati magici

Che in realtà l'argomento lo affronterò al contrario, ma il titolo così mi suonava meglio!

---

I quadrati magici sono tra i più noti e antichi rompicapi matematici. Testimonianze dei primi quadrati magici sono state ritrovate sin dai primi secoli dopo Cristo, ma c'è chi ritiene che risalgano a diversi secoli prima, forse addirittura al IV secolo a.C.
Tra i più antichi quadrati magici fin qui ritrovati ci sono i luoshu, o lo shu, cinesi, quadrati che vanno dall'ordine 3 fino al 10 (l'ordine è il numero di righe o colonne del quadrato).
In poche parole un quadrato magico è una disposizione di numeri interi tutti diversi uno dall'altro all'interno di una griglia quadrata. La somma dei numeri lungo ciascuna riga e colonna e lungo le due diagonali principali è una costante, detta "costante magica".
Per riempire un quadrato $n \times n$ servono, come ovvio, $n^2$ numeri interi. Se vengono utilizzati tutti i numeri da 1 a $n$, allora il quadrato si dice perfetto.
Per questi quadrati vale la seguente formula per il calcolo della costante magica:

Matematica, lezione 56: La teoria di Galois

Nel 52.mo volume della collana Matematica, avevo citato velocemente i risultati ottenuti da Evariste Galois nella sua trattazione matematica sulle equazioni dal quinto grado in su. In particolare il risultato più importante ottenuto dal giovane talento matematico era che in generale un'equazione polinomiale dal 5.o grado in su non è risolubile con le usuali operazioni di somma, moltiplicazione ed estrazione di radice (il fatto che sia "in generale" implica che esistono alcune equazioni particolari risolubili in questo modo). Tale risultato, che può essere formalizzato con un teorema matematico, è la conclusione del volume 56, Teoria di Galois, di Francesco Zerman, che affronta in termini moderni la teoria sviluppata dal giovane rivoluzionario francese.
L'approccio di Zerman è quanto di meglio ci si possa attendere: inizia costruendo e consolidando tutti gli strumenti necessari per comprendere la dimostrazione finale, che così diventa lunga appena mezza paginetta, ma risulta ricca di significati, soprattutto per ciò che nel frattempo ha costituito il bagaglio di tale dimostrazione. E' fuor di dubbio che, proprio come il 52.mo volume, anche questo non è di semplice lettura, ma devo dire che mi sono decisamente trovato un po' a casa tra le sue pagine, ed è diventato abbastanza facilmente uno dei miei preferiti della collana, anche in forza della pagina dei giochi.
Zerman, infatti, decide di affrontare il tema dell'infinito, proponendo al lettore sei paradossi, alcuni ben noti a tutti gli amanti della matematica divulgativa e ricreativa, altri un po' meno, ma comunque tutti stimolanti e molto ben spiegati nella pagina delle soluzioni. Tra l'altro uno dei paradossi proposti da Zerman si ricollega con la figura che viene raccontata da Veronica Giuffré nella sezione biografica: Evangelista Torricelli. La scelta, tra l'altro, completa il ponte con il 52.mo volume, poiché Torricelli è indubbiamente uno dei più noti e talentuosi allievi di Galileo Galilei. Per cui se avete preso anche solo il n.52, non potete non recuperare anche il 56!

Topolino #3615: M per Maschere

Storicamente i capitani di ventura erano i capitani delle compagnie militari mercenarie che venivano assoldati dai regni cittadini per la difesa dei propri confini. Poiché concedevano i propri servigi al miglior offerente, poteva capitare che si trovavano a combattere ora a favore ora contro le città che li assoldavano. A volte, però, alcuni di loro giungevano, spesso con la forza, a comandare direttamente le città, come per esempio Francesco Sforza e la sua casata in quel di Milano. E qualcosa del genere vuole fare anche Capitan Bassotto nel terzo atto di Maschere di Andrea Malgeri, come rivela al doge Cormoran all'inizio di un drammatico confronto a fil di spada.

Wonder Woman: i racconti classici

Nell'ottobre del 1940 lo psicologo William Moulton Marston, sulle pagine della rivista Family Circle, discusse delle potenzialità dei comic book. L'articolo catturò l'attenzione di Max Gaines, publisher per la National Periodicals e la All-American Publications, che decise di contattare l'inventore del poligrafo per invitarlo a creare per le sue riviste un nuovo supereroe. A quel punto, su suggerimento della moglie Elizabeth, anch'essa psicologa, propose il personagio di Wonder Woman. La supereroina fece così il suo esordio sulle pagine di All Star-Comics #8 dell'ottobre del 1941, disegnata da Harry George Peter.

Guardarsi intorno: Galileo, materia oscura e spazi di Hilbert

Avevo già deciso che dovevo dedicare uno dei link post di ricerca (spero di trovare presto un nome sotto cui raccogliere questa serie) a, dicamo così, cose mie, articoli legati a persone che conosco o ho conosciuto, come l'articolo da cui partiamo, Group theoretical derivation of the minimal coupling principle. L'autore, Giuseppe Nisticò, è stato il mio supervisore di dottorato (per me è stato quello principale, ma tecnicamente non era lui: storia lunga). Nell'articolo approfondisce alcuni aspetti del principio di minimo accoppiamento, che coinvolge solo la distribuzione di carica (elettrica, per esempio), escludendo i momenti di di- o di multi-polo. Il tutto, dal punto di vista della teoria dei gruppi, coinvolge il gruppo delle trasformazioni di Galileo, che sono associate all'equazione di Schrodinger (per chi ha letto il 52.mo volume di Matematica queste cose non dovrebbero essere completamente nuove).

Le grandi domande della vita: Pi e il problema della fermata

Forse una delle domande più interessanti tra quelle cui sono incappato nell'ultimo periodo su Quora: la differenza tra $\pi$ e la costante di Chaitin in termini di computabilità.
La costante di Chaitin, introdotta da Gregory Chaitin, è stata una delle protagoniste del bel volume Darwin alla prova, testo sull'evoluzione, ma anche sulla matematica, e successivamente ne ho scritto all'interno del post sull'immortalità quantistica.
Vale, però, la pena rivedere la sua definizione.

WikiRitratti: Emma Haruka Iwao

Quando uscì l'Astrocuriosità di marzo 2024 non potevo immaginare che il record delle cifre decimali del pi greco sarebbe stato battuto di lì a poco, il 14 marzo del 2024, da Jordan Ranous, Kevin O’Brien e Brian Beeler, che poi avrebbero raddoppiato il numero di cifre pochi mesi più tardi, il 28 giugno, anche questa data significativa essendo il tau day. Tra l'altro già Ranous il 18 aprile del 2023 aveva replicato il record di 10¹⁴, ovvero 100 trilioni di cifre decimali del $\pi$ raggiunto il 21 marzo del 2022 da Emma Haruka Iwao, che avevamo già incontrato in Universo pi insieme con i fratelli Chudnovsky.

Pi day 2025: Tutti a raccolta!

Anche se un po' in ritardo rispetto a quel che avrei voluto, ecco l'annuncio ufficiale che chiama a raccolta i matematti, sia quelli soliti sia quelli che normalmente non partecipano al Carnevale della Matematica, a segnalarmi i loro articoli a tema matematico realizzati tra la metà febbraio e la metà marzo 2025. La deadline è, come sempre, il 12 marzo. Nell'e-mail vi ricordo di indicare il titolo, il link e una breve descrizione. Per il tema, ovviamente il protagonista principale è il pi greco, ma va bene qualunque altro genere di post, a patto che la matematica sia, comunque, protagonista.
Qui sotto un'immagine con l'indirizzo e-mail cui scrivermi. In alternativa potete scrivermi sia nel fediverso su mastodon.social, sia su instagram. Solito nick: ulaulaman.
Buona matematica a tutti!

Matematica, lezione 55: Teoria dei frame

La teoria dei frame è relativamente giovane. Risale alla fine degli anni Quaranta, inizi dei Cinquanta del XX secolo. L'elemento più interessante di tale teoria, almeno leggendo il volume di Pierluigi Vellucci, è l'uso di basi di vettori differenti da quella ortonormale standard per descrivere e generare uno spazio vettoriale. In effetti qualcosa del genere la si vede, sia a scuola sia all'università, ma non viene mai approfondita in maniera formale. L'approccio di Vellucci, però, per quanto molto tecnico, permette di avere un'idea di come delle basi non standard, e persino delle basi ridondandi, ovvero con un numero di vettori superiore alla dimensione dello spazio vettoriale, possono essere utili in alcune applicazioni.
Altro elemento interessante della teoria è il legame tra queste basi e le trasformate di Fourier, solo che questo, poi, suggerisce Vellucci nel voler raccontare il principio di indeterminazione di Heisenberg attraverso le trasformate di Fourier stesse. La cosa, di per sé, è interessante, ma visto che alla fine le basi non standard non rientrano nel discorso, non si coglie il legame con la teoria dei frame. Il che, forse, è un po' un peccato.
Per quel che riguarda i giochi, vellucci adotta lo stesso approccio di Maurizio Codogno per il suo ultimo libro per questa collana: trarre i problemi da una newsletter matematica, nello specifico quella della European Mathematical Society. Interessanti, non dico di no, ma poco aderenti allo spirito di matematica ricreativa che aveva accomunato i giochi matematici fin qui realizzati anche a partire dal 52.mo volume.
Infine, per la biografia, Veronica Giuffré ci racconta la vita di Claude Shannon, famoso per la teoria dell'informazione e per il suo interesse pionieristico, insieme con Alan Turing, per quella che oggi chiamiamo intelligenza artificiale.

Topolino #3614: Carnevale a Venezia

Con il secondo episodio di Le maschere, Andrea Malgeri ci trasporta nell'atmosfera più sfrenata dal Carnevale, riuscendo a sviluppare al contempo le due linee narrative principali: quella dei figuranti di strada, che erano protagonisti proprio in eventi come il Carnevale, e quella della lotta contro i soprusi. A guidare il lettore attraverso queste due linee narrative ci pensa, però, un unico personaggio, il doge di Venezia Cormoran, che finisce per vivere, grazia a uno scambio che viene direttamente da Il principe e il povero, il Carnevale della sua città sia sul palco dei teatranti di strata, sia sopra i tetti in compagnia delle Maschere.
Ne emerge un personaggio interessante che grazie a questa doppia visione e al bagno di umiltà che ne consegue, giunge alla consapevolezza della stato in cui versano i veneziani a causa dela sua "distrazione" nei confronti della condotta dei Bassotti.
Altro elemento non trascurabile è la storia delle origini delle Maschere, raccontata dalla viva voce di Paperino. Storia che si intreccia con uno dei principali compiti del far ridere: spingere le persone a riflettere sul mondo. E in particolare, tramite la satira, che è prettamente politica, sui comportamenti dei governanti. E questa serie si sta rivelando un modo molto intelligente per spingere i lettori a riflettere su questo tema, senza dover necessariamente porre espliciti riferimenti all'attualità politca.

Beast World: Metafora del mondo moderno

Come scritto all'inizio di Crisi oscura sulle Terre infinite, dopo la conclusione di questa saga la Justice League decise di sciogliersi e lasciare la protezione del pianeta ai Titans guidati da Nightwing, ovvero Dick Grayson, il primo Robin. Per cui anche il crossover successivo, Beast World, vede Nightwing e i Titans protagonisti assoluti della vicenda.
Tom Taylor, scrittore della acclamata nuova serie con Dick protagonista (che ho inziato a leggere proprio in concomitanza dell'uscita di Beast World) e della nuova serie Titans, affiancato da Ivan Reis (e nel finale da altri validi disegnatori) ha costruito una storia che al tempo stesso rende protagonisti i Titans e il loro capo, ma che è anche un vero e proprio prologo al crossover successivo, ma di questo ne "parleremo" a tempo debito.